本文转载自:https://blog.cs
一、2D Simplex Noise
这次我们不打算从1D做起而是直接从2D Simplex Noise做起,不是因为Simplex Noise不能实现1D噪声,而是应用中2D、3D、4D用得更多一些。从前面的学习中,我们将Simplex Noise生成算法分成四个步骤,本文将继续采用这种分步实现的模式。
(一)、坐标变换(Coordinate skewing)。
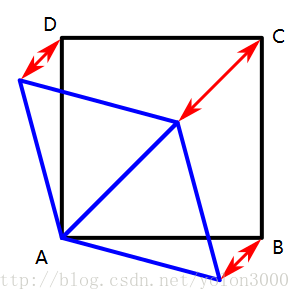
根据变换公式,我们可以很容易的实现顶点在单形与其对应的正超晶格之间进行变换。在代码中,我们用大写表示正超晶格的点及变量,用小写表示单形点及变量,相应的代码如下,这段代码上半部分即是将单形变换到对应的正超晶格中,下半部分将正超晶格变换到单形中,从前面的学习中我们已经学习了变换公式,因此,这段代码还是比较好理解的。其中,I0、J0即是正超晶格最左下角的顶点坐标(下图中的A点),dx0、dy0即为输入点到最左下角顶点的距离。
double F2 = 0.5 * (Math.Sqrt(3.0) - 1.0);
double X = x + (x + y) * F2;
double Y = y + (x + y) * F2;
int I0 = GetFloor(X);
int J0 = GetFloor(Y);
double G2 = (3.0 - Math.Sqrt(3.0)) / 6.0;
double i0 = I0 - (I0 + J0) * G2;
double j0 = J0 - (I0 + J0) * G2;
double dx0 = x - i0;
double dy0 = y - j0;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
(二)、确定单形(Simplicial subdivision)。
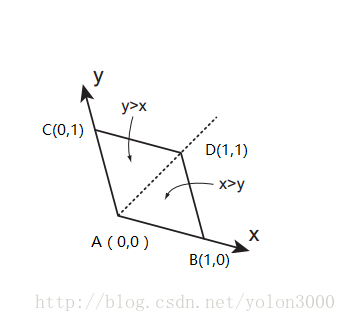
在2D中,确定单形还是比较简单的,在2D中,x 〉y时,所处的单形肯定是组成正方形的两个三角形中的下面那个,x〈 y时则相反。即我们从A(0,0)开始,如果x 〉y,则B(1,0)点,如果x〈 y,则C(0,1)点,最后到D(1,1),以此决定的三角形就是输入点所在三角形。 代码如下:
int I1, J1;
if (dx0 > dy0) { I1 = 1; J1 = 0; } else { I1 = 0; J1 = 1; }- 1
- 2
(三)、梯度值选择(Gradient selection)。
这步与Perlin 噪声生成一样,通过permutation得到梯度的索引。
int g0 = p[(I0 & 255) + p[J0 & 255]] % 8;
int g1 = p[(I0 & 255) + I1 + p[(J0 & 255) + J1]] % 8;
int g2 = p[(I0 & 255) + 1 + p[(J0 & 255) + 1]] % 8;- 1
- 2
- 3
(四)、求和(Kernel summation)。
在求和之前,我们还有一点事要做,那就是求出输入点到其他两个单形顶点的距离,这里我们给出求距离的代码,在下节中具体讲解其由来。
double dx1 = dx0 - I1 + G2;
double dy1 = dy0 - J1 + G2;
double dx2 = dx0 - 1.0 + 2.0 * G2;
double dy2 = dy0 - 1.0 + 2.0 * G2;- 1
- 2
- 3
- 4
根据前文的求和公式,求和也比较简单,我们编写代码如下:
double t0 = 0.5 - dx0 * dx0 - dy0 * dy0;
if (t0 < 0) n0 = 0.0;
else
{
t0 *= t0;
n0 = t0 * t0 * DotProduct(gradients[g0, 0], gradients[g0, 1], dx0, dy0);
}
double t1 = 0.5 - dx1 * dx1 - dy1 * dy1;
if (t1 < 0) n1 = 0.0;
else
{
t1 *= t1;
n1 = t1 * t1 * DotProduct(gradients[g1, 0], gradients[g1, 1], dx1, dy1);
}
double t2 = 0.5 - dx2 * dx2 - dy2 * dy2;
if (t2 < 0) n2 = 0.0;
else
{
t2 *= t2;
n2 = t2 * t2 * DotProduct(gradients[g2, 0], gradients[g2, 1], dx2, dy2);
}
return 70.0 * (n0 + n1 + n2);- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
DotProduct方法作用如其名。 最后,我们对各顶点点积求和后乘70以将结果归一化到[-1,1]空间中去。为什么是乘以70,下节中具体讲解。下面给出生成的Simplex噪声和分形噪声图:
二、2D Simplex Noise 实现中的理解难点
(一)、关于输入点到其他顶点的距离求取。
我们还是从图上说起。
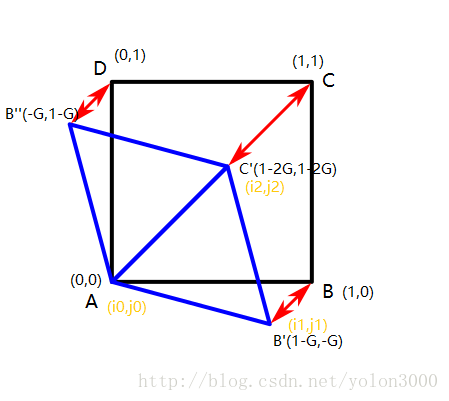
在上图中,我们设A点在变换中不变且坐标为(0,0),根据我们前文的规则,单形第二个顶点可能是B,也可能是D。如果是B,则变换后的第二个顶点B’的坐标可以由变换公式求出来为(1-G,-G),如果是D,则变换后的第二个顶点的坐标B”(-G,1-G)。观察这两个坐标,换句话说,在正超晶格中每(1,0)步相当于在单形中(1-G,-G)步,每(0,1)步相当于单形中(-G,1-G)步。或者说在单形中顶点坐标i1-i0 = I1 - G(在图中的黄色坐标,小写i,j表示在单形中的坐标,大写的I,J表示是在正超晶格中的坐标),同理j1-j0 = J1 - G。好了,现在我们求输入点到第二个的距离:
dx1 = x - i1 //x为输入点横坐标,i1为第二个顶点横坐标
= x - ( i0 + I1 - G ) //将上式 i1 - i0 = I1 - G 代入
= dx0 + i0 - ( i0 + I1 -G ) // x = i0 + dx0 输入点横坐标又可以写为i0 与 dx0 之和
= dx0 + I1 - G
同理,dy1 = dy0 + J1 - G
对于第三个坐标,我们也可以根据变换公式求出单形的顶点C坐标为(1-2G,1-2G),所以:
dx2 = x - i2
= x - ( i0 + 1 - 2G )
= dx0 + i0 - ( i0 + 1 - 2G )
= dx0 - 1 + 2G
同理,dy2 = dy0 - 1 +2G
(二)、关于求和后乘70。
关于这里的70,自己计算了一把,始终不知道怎么得到的,TODO一下
在求和返回前,我们将和乘70,为什么是70?
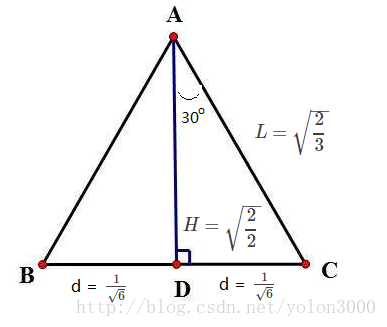
在前文中我们提到,为了将结果归一化到[-1,1]区间,这就需要我们计算n每个分量相加后的最大值并保证最大值要等于1,这就要乘一个系数,系数值取多少根据分量相加后的最大值而定,由几何学可知,当输入点在某一边中点时得到的分量相加值最大,根据前文,我们知道,等边三角形的边为 l=23−−√l=23,高为 h=2√2h=22,在等边三个形中,可以知道上半顶角为30度,所以可以求出输入点到另外两个点的距离为d=16√d=16,如下图所示:
所以,此时t=(0,13,13)t=(0,13,13)。取最大值时,梯度和距离向量的点乘结果可以认为是两者模的乘积,而梯度模的最大值为2–√2,因此最后和的最大值为:
134⋅16–√⋅2–√⋅2≈170134⋅16⋅2⋅2≈170
因此,我们最后把结果乘以70。那么,如果r2取0.6,最后需要乘以多少呢?答案大约为24.51。利用这个想法,我们可以在任意维度下计算最后的伸缩值,例如在三维下,单形,即正四面体的边长为3√232,当r2取0.5时,最后大概需要乘以31.32。
参考文献
1、Simplex noise demystified,Stefan Gustavson, Linköping University, Sweden ([email protected]), 2005-03-22
2、Simplex Noise