本文转载自:https://blog.csdn.net/yolon3000/article/details/78106203
一、Simplex Noise优势
通过前面我们的学习,知道Perlin噪声的算法复杂度为O(2^n),生成噪声维度越高,计算复杂性增长越快,同时,在实现时对Permutation表的操作也越复杂,插值运算也越多,代码操作时难度也越来越大。正是因为如此,2001年,ken perlin对Perlin噪声进行了改进,希望凭借新的理论解决高维度的噪声生成计算量的问题,克服了Perlin噪声的很多缺点,这次改进基于的数学基础是单形(Simplex),所以最后的噪声就叫作Simplex Noise。概况起来说,相比原始的Perlin噪声,Simplex 噪声有以优势。
1、Simplex 噪声生成时复杂度得到降低,乘法运算减少。
2、Simplex 噪声生成算法复杂度为O(n^2),较原始Perlin 噪声 O(2^n)的计算复杂度有所降低,特别在高维度时表现更为出色。
3、Simplex 噪声因其无缝重复性可以在大范围内随意扩展。
4、Simplex 噪声没有明显方向性的人工痕迹(各向同性),虽然各方向生成的噪声看起来不一样。
5、Simplex 噪声有定义良好处处连续的计算更简单的梯度值。
6、Simplex 噪声有良好的硬件亲和性。
Simplex噪声复杂度的降低来源于对晶格的选取,因单形固有的性质可以使计算的梯度值大大减少从而大幅降低了计算量。
二、单形(Simplex)
(一)、单形
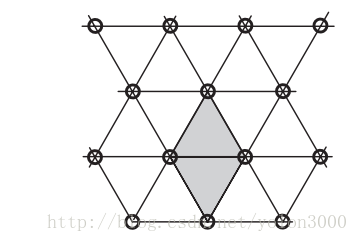
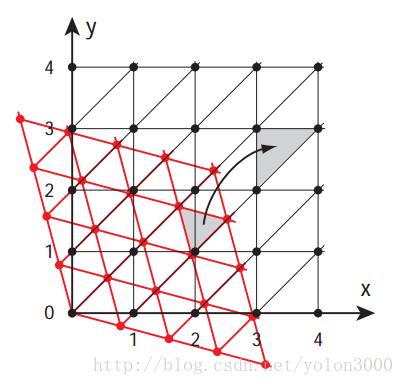
单形是线段、三角形、四面体直至任意维度符号的一种概述,是N-space的一种细分。简单说,N维单形就是能铺满N维空间的最简单图形。对1D空间来说,单形就是等长的线段,可以通过线段的首尾相连让它平铺整个1D空间,对2D空间来说,能平铺整个空间的最简单图形是等边三角形,对3D空间来说,能平铺整个空间的最简单图形是四面体,依此类推度。单形有一个特性,N维空间的单形有N+1个顶点,N!个单形能组成N维空间的超晶格体。在2D空间中,单形晶格可以表示如下:
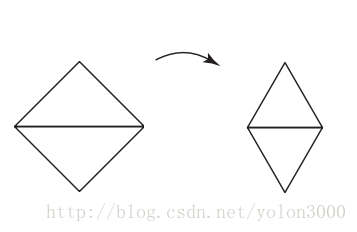
两个单形组成2D空间的菱形(如图灰色部分显示),这个菱形可以看成是2D空间的超晶格体正方形沿水平方向挤压,直到对角线长度与边长一样,如下图所示。
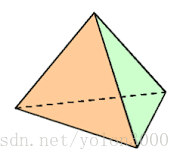
3D空间的单形是四面体。
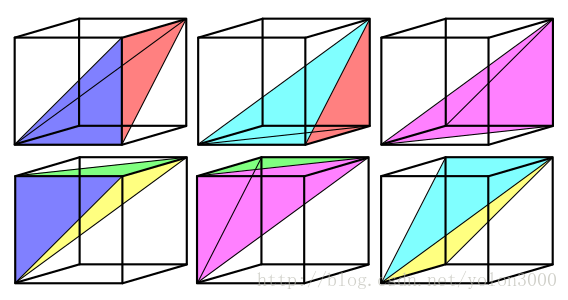
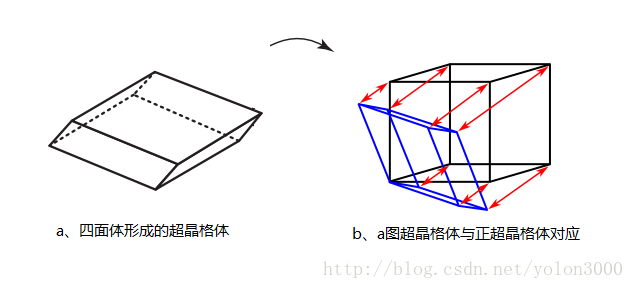
6个四面体组成3D空间的超晶格体。
需要注意的是,6个四面体组成超晶格体不是正超晶格体,6个四面体形成的超晶格体如下图中a所示,它与正超晶格体的对应与下图b所示,其可以看成是正超晶格体在主对角线上挤压,直到主对角线长度与边长一样。
类推到4D及高维空间,N维空间的单形有N+1个顶点,N!个单形能组成N维空间的超晶格体。在Perlin噪声生成中,我们计算定点梯度时的顶点数为2^n个,而使用单形后,定点个数降为N+1个,所以Simplex噪声算法复杂度得以大幅下降,特别是在高维生成噪声时。
(二)、单形与超晶格
之前我们一直在强调,N维空间的N!个单形可以组成N维空间的超晶格体,这个超晶格体可以看成是N维空间中正超晶格体在一个对角线上挤压形成,换句话说就是N维空间的单形跟N维空间的正超晶格体是存在联系的,事实上确实存在联系,将超晶格体偏斜(skewing)可以得到正超晶格体,下图为2D空间下的示意。
通过偏斜(skewing),我们可以得到原超晶格体坐标与正超晶格体坐标之间的对应关系:
x′=x+(x+y+...)∗Fx′=x+(x+y+...)∗F
y′=y+(x+y+...)∗Fy′=y+(x+y+...)∗F
而
F=n+1−−−−−√−1nF=n+1−1n
x,y为原超晶格体的坐标,x’,y’为正超晶格体的坐标。同样,我们可以推出正超晶格体到原超晶格体的坐标变换公式:
x=x′−(x′+y′+...)∗Gx=x′−(x′+y′+...)∗G
y=y′−(x′+y′+...)∗Gy=y′−(x′+y′+...)∗G
而
G=1−1/n+1−−−−−√nG=1−1/n+1n
x,y为原超晶格体的坐标,x’,y’为正超晶格体的坐标。这两个计算公式是下步计算的基础。
例,在2D空间时:
x′=x+(x+y)∗Fx′=x+(x+y)∗F
y′=y+(x+y)∗Fy′=y+(x+y)∗F
其中
F=3–√−12F=3−12
x=x′−(x′+y′)∗Gx=x′−(x′+y′)∗G
y=y′−(x′+y′)∗Gy=y′−(x′+y′)∗G
其中
G=1−1/3–√2=3−3–√6G=1−1/32=3−36
在3D空间时:
x′=x+(x+y+z)∗Fx′=x+(x+y+z)∗F
y′=y+(x+y+z)∗Fy′=y+(x+y+z)∗F
z′=z+(x+y+z)∗Fz′=z+(x+y+z)∗F
其中
F=4–√−13=13F=4−13=13
x=x′−(x′+y′+z′)∗Gx=x′−(x′+y′+z′)∗G
y=y′−(x′+y′+z′)∗Gy=y′−(x′+y′+z′)∗G
z=z′−(x′+y′+z′)∗Gz=z′−(x′+y′+z′)∗G
其中
G=1−1/4–√3=16G=1−1/43=16
(三)、坐标变换
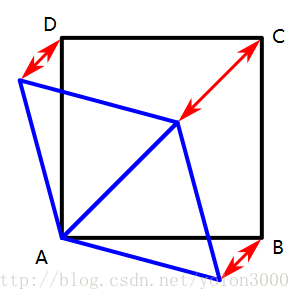
上一节我们给出了单形和正超晶格之间的坐标变换公式,下面我们以2D空间为例来具体讲解在2D空间下,单形与正方形晶格之间的变换计算。
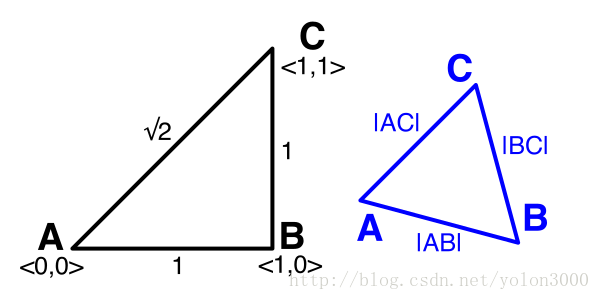
如上图所示,我们在变换时固定A点,通过偏斜(skewing)可以从菱形变换到正方形,当然也可以从正方形变换到菱形。在正超晶格中定义A(0,0),B(1,0),C(1,1),在变换后,A保持不变,根据变换公式变换到单形后的点,下图蓝色等边三角形A(0,0),B(1-G,-G),C(1-2G,1-2G)。
同时利用
|AB|2=|A−B|2=|(0,0)−(1−G,−G)|2=2G2−2G+1|AB|2=|A−B|2=|(0,0)−(1−G,−G)|2=2G2−2G+1
且
G=3−3–√6G=3−36
可以得到等边三角形的边长为:
L=23−−√L=23
还可以得到等边三角形的高:
H=23−−√∗3–√2=22−−√H=23∗32=22
在3D空间变换类似。
三、Simplex Noise算法
Simplex噪声是在Perlin噪声基础上改进而来,因此其基本原理不变,但相比Perlin噪声,Simplex噪声算法主要有两个方面的改进:
1、使用单形而不是正超晶格体使输入点需要计算的顶点数大幅减少。
2、使用一个衰减函数计算顶点梯度贡献值,并对所有顶点贡献值求和来改进Perlin噪声生成时的插值计算,使得在高维时减轻计算压力和理解难度。
Simplx噪声与Perlin噪声一样也是梯度噪声,这没有变。在我们算法中,我们采用四步来计算Simplex噪声。
第一步:坐标变换(Coordinate skewing)。通过偏斜(skewing)将单形坐标变换到对应空间的正超晶格体空间中,变换公式上一节已给出。为什么要变换到正超晶格体空间中呢,原因是在正超晶格体中,我们更容易找到输入点所处的晶格,从而确定所处晶格的顶点坐标 (xb’=floor(x’), yb’=floor(y’), …),只有得到顶点坐标,我们才能得到顶点坐标上的梯度值和输入点到各顶点的距离 (xi’=x’-xb’, yi’=y’-yb’, …)。
第二步:确定单形(Simplicial subdivision)。前文我们说过,在N维空间中,N!个单形晶格体可以组成一个正晶格体,反过来说,通过第一步,我们可以确定我们输入点所在的正超晶格体,但是这个正超晶格体包括着N!个单形晶格体,为了得到单形的顶点,我们还必须确定输入点所处的单形晶格体。先以2D为例:
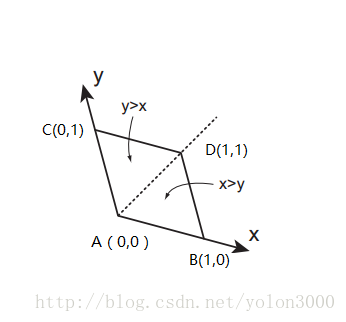
这非常好理解,在2D中,x 〉y时,所处的单形肯定是组成正方形的两个三角形中的下面那个,x〈 y时则相反。即我们从A(0,0)开始,如果x 〉y,则B(1,0)点,如果x〈 y,则C(0,1)点,最后到D(1,1),以此决定的三角形就是输入点所在三角形。
推广到N维空间中,我们从全0的坐标开始,然后找到所有轴中最长的在该轴所在位置加1形成第二个坐标点,然后再在剩余轴中取最长的并在该轴所在位置加1形成第三个坐标点,以此类推,至到全1的坐标结束,这样就得到了输入点所在单形了。例如点(0.3,0.7,0.5,0.2),为确定其所在单形,从(0,0,0,0)开始,先找到最大的0.7,这在y轴上,所以第二个顶点为(0,1,0,0),再找最大的0.5,对应顶点(0,1,1,0),再找最大的0.3,对应(1,1,1,0),最后就是(1,1,1,1),这就是我们要找的单形了。
第三步:梯度值选择(Gradient selection)。通过上一步,我们得到了单形的顶点,这一步就是得到存储在顶点上的梯度值,与Perlin噪声是一样的,也是通过以permutation排列表为索引得到顶点梯度值。
第四步:求和(Kernel summation)。Simplex利用求和替代了Perlin噪声的插值,使用一个精心选择的径向衰减函数对每个顶点的贡献值进行计算然后求和,计算顶点贡献值的函数如下:
(max(0,r2−d2))4∗(<Δx,Δy,...>⋅<grad.x,grad.y,...>)(max(0,r2−d2))4∗(<Δx,Δy,...>⋅<grad.x,grad.y,...>)
或者可以写为:
(max(0,r2−|dist|2))4×dot(dist,grad)(max(0,r2−|dist|2))4×dot(dist,grad)
其中,dist是输入点到该顶点的距离向量,grad是该点存储的伪随机梯度向量,r^2的取值是0.5或0.6。取0.5时可以保证没有不连续的间断点,取0.6得到更好的视觉效果。0.6也是Ken Perlin在算法中引用的值。求和后我们通常还会将结果归一化到[-1,1]空间中去。
参考文献
1、Real-Time Shading SIGGRAPH Course Notes, Perlin K. Noise hardware[J].,2001.
2、Simplex noise demystified,Stefan Gustavson, Linköping University, Sweden ([email protected]), 2005-03-22
3、Simplex noise
4、谈谈噪声
5、Simplex Noise