Xgboost近似分位数算法

一、近似算法

（二）提升树模型：Xgboost原理与实践这篇博客介绍了XGBoost使用exact greedy算法来寻找分割点建树，但是当数据量非常大难以被全部加载进内存时或者分布式环境下时，exact greedy算法将不再合适。因此作者提出近似算法（Approximate Algorithm）来寻找分割点。

近似算法的大致流程见下面的算法（参考文献【5】中3.2）。

对于某个特征 $k$，算法首先根据特征分布的分位数找到切割点的候选集合 $S_k = \{s_{k1}, s_{k2}, ... ,s_{kl} \}$；然后将特征 $k$的值根据集合 $S_k$划分到桶(bucket)中，接着对每个桶内的样本统计值G、H进行累加统计，最后在这些累计的统计量上寻找最佳分裂点。

不同于基本的穷举算法，paper指出两种近似算法：一种是全局算法，即在初始化tree的时候划分好候选分割点，并且在树的每一层都使用这些候选分割点；另一种是局部算法，即每一次划分的时候都重新计算候选分割点。这两者各有利弊，全局算法不需要多次计算候选节点，但需要一次获取较多的候选节点供后续树生长使用，而局部算法一次获取的候选节点较少，可以在分支过程中不断改善，即适用于生长更深的树，两者在effect和accuracy做trade off。

论文【5】实验中发现，全局k分位点取20和局部k分位点取3，得到了近似的效果。

！！！从算法伪代码可以看出近似算法的核心是如何根据分位数采样得到分割点的候选集合 $S$。 Xgboost提出了Weighted Quantile Sketch来解决这个问题。

在讲述Weighted Quantile Sketch之前，必须先要介绍一下什么是Quantile。这是Weighted Quantile Sketch的关键，如果不理解Quantile，就不会理解，在当数据量非常大难以被全部加载进内存时或者分布式环境下时，Xgboost的近似算法是如何寻找分割点的候选集合 $S$的。

二、 Quantile

2.1 $\phi$-quantile

输入数据： 14, 19, 3, 15, 4, 6, 1, 13, 13, 7, 11, 8, 4, 5, 15, 2

则排序后，该组数据为： 1, 2, 3, 4, 4, 5, 6, 7, 8, 11, 13, 13, 14, 15, 15, 19. 如下图所示：

在上面的序列中，

第1小的数是什么？ 很明显是：1 (rank=1)
第4小的数是什么？ 答案是：4 (rank=4)
第50%小的数是什么？ 50% * 16 = 8（rank=8)， 则答案为：7

什么是分位点呢？ $\phi$-quantile表示 $rank=\lfloor \phi \times N \rfloor$的元素，其中，N为序列中元素的个数。例如，在上面的例子中：

0.25-quantile是什么？ rank=0.25×16=4，所以答案为：4
0.5-quantile是什么？ rank=0.5×16=8，所以答案为：7

2.2 $\epsilon$-approximate $\phi$-quantiles

$\epsilon$-approximate $\phi$-quantiles的意思就是：在 $\phi$-quantiles误差 $\epsilon$-approximate以内位置的取值。即近似分位点。

即 $\phi$-quantiles是在区间 $[ \lfloor (\phi - \epsilon) \times N \rfloor, \lfloor (\phi + \epsilon) \times N \rfloor]$，而不是之前的精确的 $\lfloor \phi \times N \rfloor$。还是上面的例子，令 $\epsilon=0.1$， $\phi=0.5$，由数据可知 $N=16$，此时 $[ \lfloor (\phi - \epsilon) \times N \rfloor, \lfloor (\phi + \epsilon) \times N \rfloor]$为[6.4,9.6]，即rank为 $\{7,8,9\}$，0.1-appoximate 0.5-quantile为： $\{6,7,8\}$。

这个物理含义是什么呢？就是说，如果我们允许 $\epsilon*N$就是1.6的误差的话，那么0.5-quantile的值为6，7或者8都可以。都算对。详见参考文献【1】。

2.3 $\epsilon$-approximate quantile summary

我们已经可以看到，即便是求一个序列的 $\epsilon$-approximate $\phi$-quantiles，也必须先对数据进行排序，而如果我们的内存不足以让全部数据排序时，应该怎么解决？早在2001年，M.Greenwald和S. Khanna提出了GK Summay分位点近似算法（ $\epsilon$-approximate $\phi$-quantiles）【2】，直到到2007年被Q. Zhang和W. Wang提出的多层level的merge与compress/prune框架进行高度优化，而被称为A fast algorithm for approximate quantiles【3】，目前XGBoost框架套用A fast algorithm算法结构。

GK Summay巧妙地设计了 $\epsilon$-approximate quantile summary 。 $\epsilon$-approximate quantile summary 是一种数据结构，该数据结构能够以 εN的精度计算任意的分位查询。当一个序列无法全部加载到内存时，常常采用quantile suammary近似的计算分位点。

大致来讲下思路： $\epsilon$-approximate quantile summary这个数据结构不需要一次存入所有的数据，它先用一些元组存入部分数据（当然在内部需要排序），这些元组记录的是现有的value值和一些位置信息，有了这些信息，就保证了能够以 εN的精度计算任意的分位查询。只要流式系统中每个时刻都维持这种summary结构，每次查询都能满足精度要求，但是流式数据实时更新，需要解决新增数据的summary更新问题。为此，算法提供了insert操作，insert操作可以保证现有的summary结构仍然可以保证 εN的精度。当然，每次数据插入都需要新增元组，summary结构不能持续增加而不删除，因此到达一定程度需要对summary进行delete。同时，delete操作也可以保证现有的summary结构仍然可以保证 εN的精度。
其实整个算法比较复杂，详见参考文献【1】【4】。建议认真阅读【1】。

到这里，我们已经知道，有了 $\epsilon$-approximate quantile summary这个数据结构，无论多大的数据，我们只要给定查询的rank值，就可以得到误差在 εN以内的近似分位点。

三、Weighted Datasets

现在我们回到Xgboost中，在建立第 $i$棵树的时候已经知道数据集在前面 $i−1$棵树的误差，因此采样的时候是需要考虑误差，对于误差大的特征值采样粒度要加大，误差小的特征值采样粒度可以减小，也就是说采样的样本是需要权重的。

重新审视目标函数
$\sum_i\left[L(y_i,\hat{y}_i^{K-1})+g_if_K(x_i)+\frac{1}{2}h_if_K^2(x_i)\right]+\Omega(f_K)+constant \tag 1$

通过配方可以得到：
$\sum_{i} \left[ \frac {1}{2} h_i \left( f_K(x_i) - (-g_i/h_i)\right)^2 \right] + \Omega (f_K) + constant\tag 2$

因此可以将该目标还是看作是关于标签为 ${-{g_i}/{h_i}}$和权重为 $h_i$的平方误差形式。 $h_i$为样本的二阶导数。

3.1 二阶导数h为权重的解释

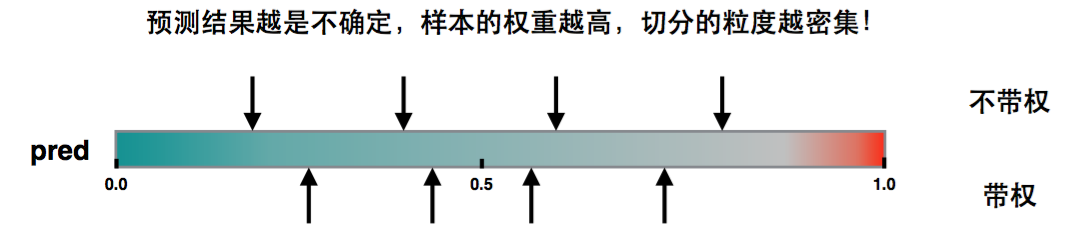
如果损失函数是Square loss，即 $Loss(y, \widehat y) = (y - \widehat y)^2$，则 $h=2$，那么实际上是不带权(每个样本的权重一样)。 如果损失函数是Log loss，则 $h=pred∗(1−pred)$. 这是个开口朝下的一元二次函数，所以最大值在 $pred=0.5$。当pred在0.5附近，值都比较大，也就是权重都比较大，在切直方图时，我们希望桶比较均匀，因此这部分就会被切分的更细。

3.2 问题转换

记
$D_k = \{(x_{1k}, h_1), (x_{2k}, h_2), \cdots (x_{nk}, h_n)\} \tag 3$

表示 每个训练样本的第 $k$维特征值和对应二阶导数。接下来定义排序函数为 $r_k(\cdot):R \rightarrow[0, +\infty)$
$r_k (z) = \frac {1} {\sum\limits_{\left( {x,h} \right) \in {D_k}} h } \sum\limits_{\left( {x,h} \right) \in {D_k},x < z} h \tag 4$

函数表示特征的值小于 $z$的样本分布占比，其中二阶导数 $h$可以视为权重。参考文献【6】有计算 $r_k (z)$的例子。
在这个排序函数下，我们找到一组点 $\{ s_{k1}, s_{k2}, ... ,s_{kl} \}$，满足：
$| r_k (s_{k,j}) - r_k (s_{k, j+1}) | < \varepsilon \tag 5$

其中， ${s_{k1}} = \mathop {\min }\limits_i {x_{ik}},{s_{kl}} = \mathop {\max }\limits_i {x_{ik}}$，ε为采样率，直观上理解，我们最后会得到1/ε个分界点。注意，这里的ε就是每个桶的比例大小。

在Xgboost官方文档中设置tree_method=approx，然后设置sketch_eps，就可以确定有多少个候选分割点。

四、Weighted Quantile Sketch

好了，如果我们的数据集比较小（特征的不同value不多），采用近似算法的话，我们只需要排序特征的所有特征值，然后根据公式（5）就可以求出候选的分割点。但是，如果这里的关键是：如果我们的数据量特别大（某些特征的不同value特别特别多），以致于无法排序找到分位点，我们应该怎么做？

对于每个样本都有相同权重的问题，本文第二部分已经介绍了有算法解决该问题。对于这种weighted datasets的情况，陈天奇博士提出了Weighted Quantile Sketch算法。Weighted Quantile Sketch算法的思想是基于参考文献【2】【3】，作者也证明该算法支持merge和prune操作，因此适合分布式场景。

Weighted Quantile Sketch的过程和证明也比较复杂，详见参考文献【5】补充材料，【8】，【9】。

有了Weighted Quantile Sketch，我们就可以求得一个大数据集每个特征的近似分位点，也就是求得了算法2中最核心的 $S_k = \{s_{k1}, s_{k2}, ... ,s_{kl} \}$。且这个近似分位点的精度是在 $ε*\sum_ih_i$之内的。 $\sum_ih_i$就是第二部分的 $N$的意思，只不过Xgboost中是Weighted Datasets。

五、参考文献

【1】ε-approximate quantiles添加链接描述
【2】Space-efficient online computation of quantile summaries
【3】A fast algorithm for approximate quantiles in high speed data streams
【4】GK Summay算法（ϵ−approximate ϕ−quantile）
【5】XGBoost: A Scalable Tree Boosting System
【6】XGBoost之分位点算法
【7】XGBoost解读(2)–近似分割算法
【8】xgboost之分位点算法