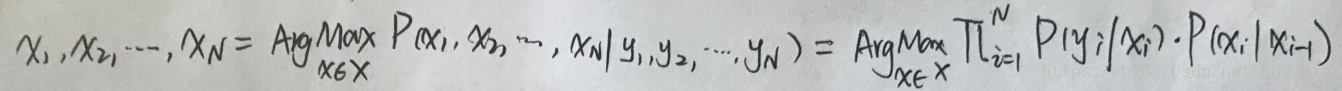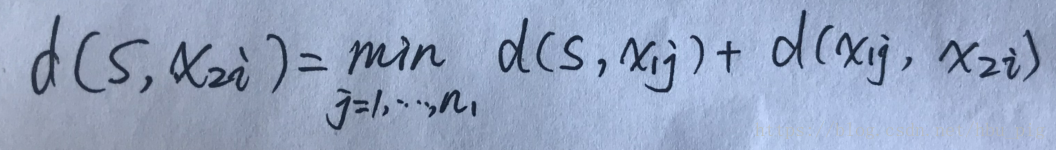简述维特比算法（Viterbi Algorithm）

维特比算法是一个特殊但应用最广的动态规划算法。利用动态规划，可以解决任何一个图中的最短路径问题。而维特比算法是针对一个特殊的图——篱笆网络（Lattice）的有向图最短路径的问题而提出的。它之所以重要，是因为凡是使用隐含马尔可夫模型描述的问题都可以使用它来解码，包括今天的数字通信、语音识别、机器翻译、拼音转汉字、分词等。下面用输入法拼音转汉字来说明。

假定用户盲打时输入的拼音是,对应的汉字是（为简单起见，以字为单位来解释维特比算法），那么隐含的状态序列即为在输出序列发生的条件下概率最大的那条序列：

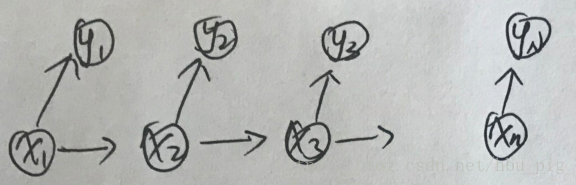
输入为可见序列，产生他们的隐含序列。下图为隐含的马尔可夫模型

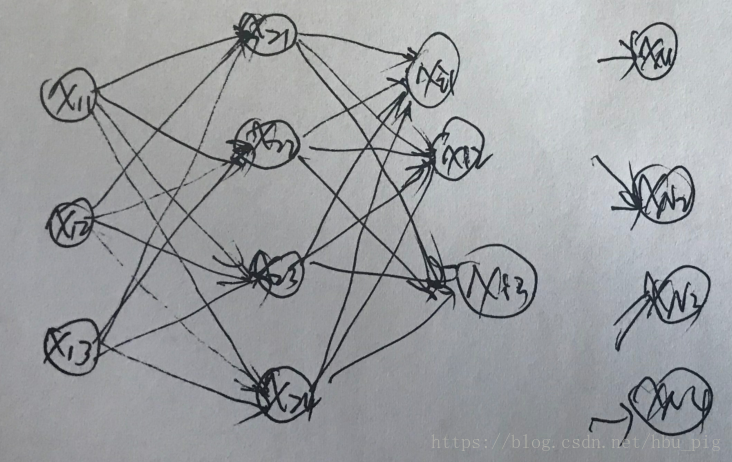
这是一个相对简单的隐含马尔可夫链，没有状态跳跃，也没有状态自环。是状态之间的转移概率，是每个状态的产生概率。现在，这个马尔可夫链的输出已固定，但是状态不固定，比如拼音“zhong”为输出，状态可能为“中”、“种”等。我们不妨抽象一点，把表示为状态的第j个可能的值。如果把每个状态按照不同的值展开，可得到下面的篱笆网络（Lattice）：

上图中每个状态可能有3,4个值，实际上它们可以有任意个值

维特比算法的基础可以概括为下面三点：

1. 如果概率最大的路径P（或者说最短路径）经过某个点，如图中的,那么这条路径上从起始点S到的这一段子路径Q，一定是S到之间的最短路径。
2. 从S到E路径必定经过第i时刻的某个状态
3. 结合上述两点，假定当我们从状态i进入到状态i+1时，从S到状态i的各个可能值的最短路径都已找到，那么只需考虑起到S到状态i各个结点的最短路径到状态i+1的各个结点的最短路径即可。

基于上述三点，维特比总结了如下算法：

第一步，从起点S出发，对于第一个状态的各个结点，不妨假定有个，计算出S的距离d（S，）

第二步，这是整个算法的关键。对于第二个状态的所有结点，要计算出S到它们的最短距离。我们知道，对于特定的结点,从S到它的路径可以经过状态1到中任何一个结点,我们需要找到这些路径的最小值。这样对于第二个状态的每个结点，需要进行次乘法运算，假定这个状态有个结点，把S到这些结点的距离都算一遍，就有次运算。

接下来，类似的从第二个状态走到第三个状态，一直走到最后一个状态，就得到了整个网格从头到尾的最短路径。每一步状态转换的复杂度为。如果假定在这个隐含马尔可夫链中结点最多的状态有D个结点，也就是这个那个网格的宽度为D，那么任何一步的复杂度不超过,由于网格长度为N，所以整个维特比算法的复杂度是.