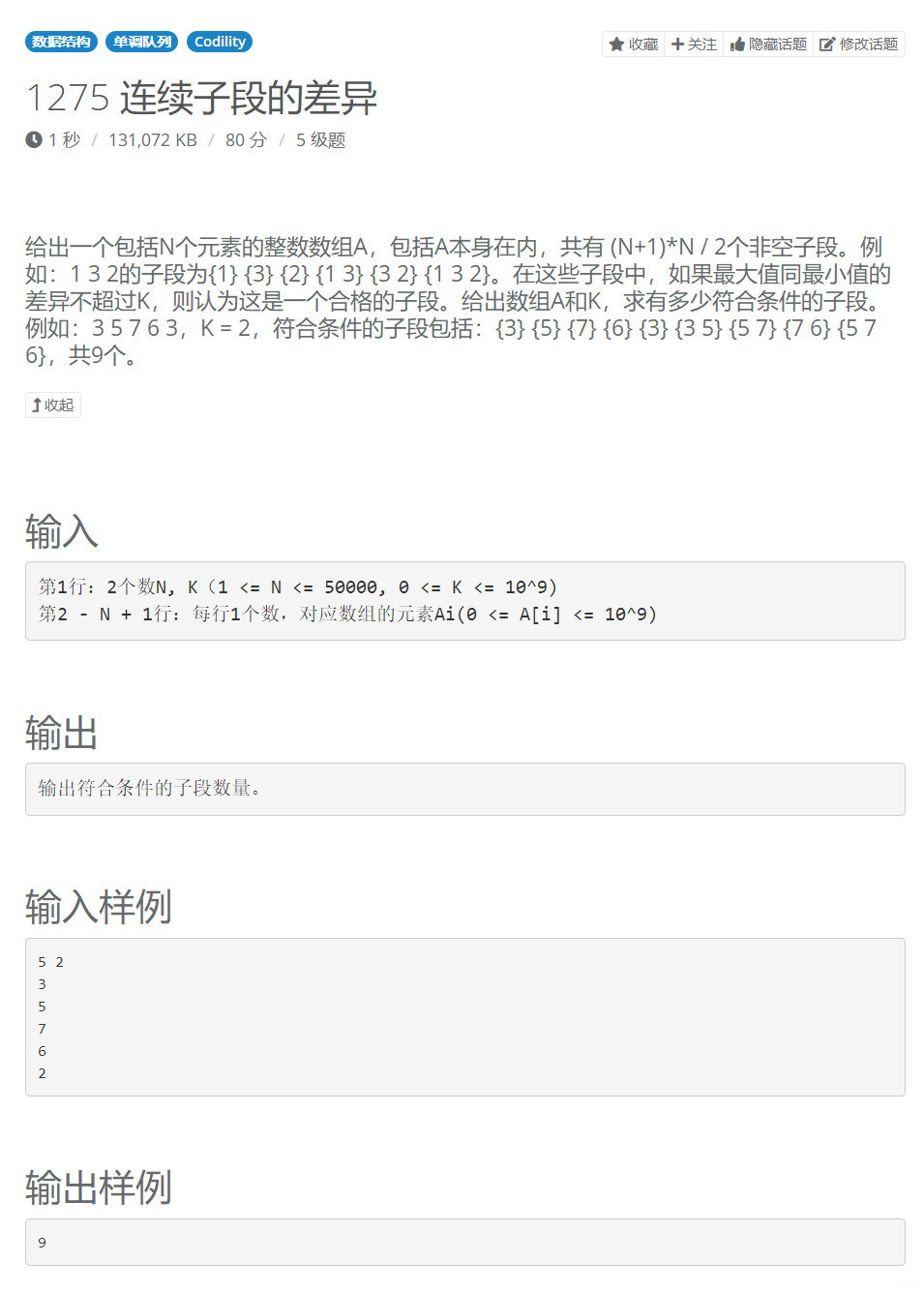
【题目描述】
【思路】
固定左端点
,向右寻找一个最远的右端点
,使得区间
中的最大值减去最小值的差
同时
中的最大值减去最小值的差
,这样一来
都符合要求,以
为左端点的区间对答案的贡献为
,因为随着
的增加,
也只能不断增加,所以可以用单调队列求区间的最大值和最小值
#include<bits/stdc++.h>
using namespace std;
const int maxn=50005;
int n,k;
int a[maxn];
deque<int> minq,maxq;
int main(){
scanf("%d%d",&n,&k);
for(int i=0;i<n;++i) scanf("%d",&a[i]);
long long ans=0;
int ri=0;
for(int i=0;i<n;++i){
while(minq.size() && minq.front()<i) minq.pop_front();
while(maxq.size() && maxq.front()<i) maxq.pop_front();
while(ri<n){
while(minq.size() && a[minq.back()]>=a[ri]) minq.pop_back();
minq.push_back(ri);
while(maxq.size() && a[maxq.back()]<=a[ri]) maxq.pop_back();
maxq.push_back(ri);
if(a[maxq.front()]-a[minq.front()]>k) break;
++ri;
}
ans+=ri-i;
}
printf("%lld\n",ans);
return 0;
}