Float类型出现舍入误差的原因(round 取位)

在练习时，输入如下代码：

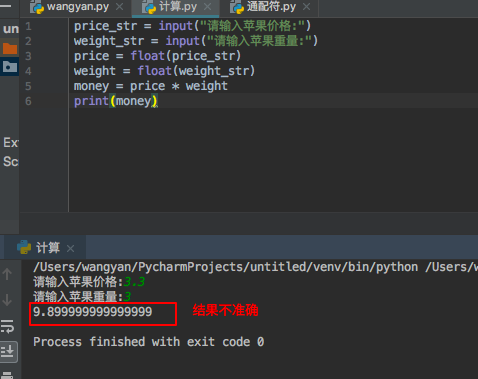
结果不准确。

原因：https://blog.csdn.net/bitcarmanlee/article/details/51179572

浮点数一个普遍的问题就是在计算机的世界中，浮点数并不能准确地表示十进制。并且，即便是最简单的数学运算，也会带来不可控制的后果。因为，在计算机的世界中只认识0与1

python中的decimal模块可以解决上面的烦恼 

decimal模块中，可以通过整数，字符串或原则构建decimal.Decimal对象。如果是浮点数，特别注意因为浮点数本身存在误差，需要先将浮点数转化为字符串。

当然精度提升的同时，肯定带来的是性能的损失。在对数据要求特别精确的场合（例如财务结算），这些性能的损失是值得的。但是如果是大规模的科学计算，就需要考虑运行效率了。毕竟原生的float比Decimal对象肯定是要快很多的。

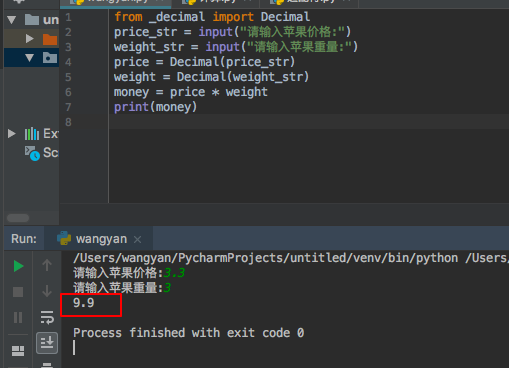
使用上述办法解决后：

知识点总结：

1. decimal模块：

Python提供了decimal模块用于十进制数学计算，它具有以下特点：

1. 提供十进制数据类型，并且存储为十进制数序列；
2. 有界精度：用于存储数字的位数是固定的，可以通过decimal.getcontext（）.prec=x 来设定，不同的数字可以有不同的精度
3. 浮点：十进制小数点的位置不固定（但位数是固定的）

首先是float累加产生误差的原因，该部分转自：http://blog.csdn.net/zhrh0096/article/details/38589067

1.  浮点数IEEE 754表示方法

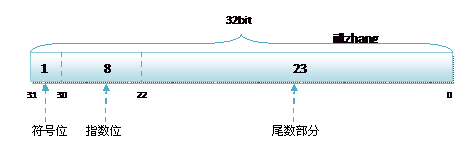
要搞清楚float累加为什么会产生误差，必须先大致理解float在机器里怎么存储的，具体的表示参考[1] 和 [2]， 这里只介绍一下组成

由上图可知(摘在[2])， 浮点数由： 符号位 + 指数位 + 尾数部分， 三部分组成。由于机器中都是由二进制存储的，那么一个10进制的小数如何表示成二进制。例如: 8.25转成二进制为1000.01, 这是因为 1000.01 = 1*2^3 + 0*2^2 + 0*2^1 + 0*2^0 + 0*2^-1 + 2*2^-2 = 1000.01.

（2）float的有效位数是6-7位，这是为什么呢？因为位数部分只有23位，所以最小的精度为1*2^-23 在10^-6和10^-7之间，接近10^-7,[3]中也有解释

那么为什么float累加会产生误差呢，主要原因在于两个浮点数累加的过程。

2. 两个浮点数相加的过程

两浮点数X，Y进行加减运算时，必须按以下几步执行（可参考 [4] 中插图）：
（1）对阶，使两数的小数点位置对齐，小的阶码向大的阶码看齐。
（2）尾数求和，将对阶后的两尾数按定点加减运算规则求和(差)。
（3）规格化，为增加有效数字的位数，提高运算精度，必须将求和(差)后的尾数规格化。
（4）舍入，为提高精度，要考虑尾数右移时丢失的数值位。
（5）判断结果，即判断结果是否溢出。

关键就在与对阶这一步骤，由于float的有效位数只有7位有效数字，如果一个大数和一个小数相加时，会产生很大的误差，因为尾数得截掉好多位。例如：

123 + 0.00023456 = 1.23*10^2 + 0.000002 * 10^2 = 123.0002

那么此时就会产生0.00003456的误差，如果累加多次，则误差就会进一步加大。

解决方式有几种，但都不是最佳方式，参考：http://bbs.csdn.net/topics/390549664

3.解决方法

方法一

Kahan summation算法

https://en.wikipedia.org/wiki/Kahan_summation_algorithm

function KahanSum(input)
var sum = 0.0
var c = 0.0 // A running compensation for lost low-order bits.
for i = 1 to input.length do
var y = input[i] - c // So far, so good: c is zero.
var t = sum + y // Alas, sum is big, y small, so low-order digits of y are lost.
c = (t - sum) - y // (t - sum) cancels the high-order part of y; subtracting y recovers negative (low part of y)
sum = t // Algebraically, c should always be zero. Beware overly-aggressive optimizing compilers!
next i // Next time around, the lost low part will be added to y in a fresh attempt.
return sum

• 1

伪代码如上

解决方法就是把多余的误差部分算出来(c)，再在下一次循环减去这个误差

方法二

int main()
{
float f = 0.1;
float sum = 0;
sum+=add(f, 4000000);
cout<<sum<<endl;
return 0;
}

float add(float f,int count)
{
if(count==1)
return f;
else
return add(f,count/2)+add(f,count-count/2);
}

• 1

二分法递归计算加法，这样会没有误差，但是函数调用消耗大（尤其是多次）

方法三

使用double，精度更高，但是本来是没有必要用这么高精度的

方法四

ieee浮点数,为了规格化,精度每超过2的整数次幂,精度要下降一位,
你的f是0.1,float位数是23,当sum足够大的时候,会出现 sum+f==sum 的情况,这个是ieee标准,
和C++没关系,事实上编译器应该已经做了浮点精度调整了,你这结果误差算小的了.
避免这种误差的方法就是浮点数,永远不要让一个很大的数去加上一个很小的数.不知你这段代码的目的是

什么,但如果你改成这样,误差会小很多: