泰勒公式
泰勒公式:

Jensen不等式
若f是凸函数,则

切比雪夫不等式
切比雪夫不等式:

切比雪夫不等式的证明过程:
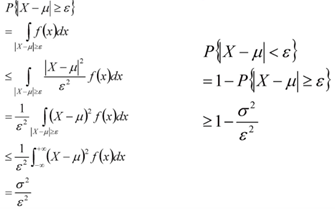
大数定理
大数定理公式:

中心极限定理

用样本估计参数
1)矩估计
样本的矩:

随机变量的矩与样本的矩有什么关系?
随机变量的矩可以理解为总体的矩,根据总体的k阶矩等于样本的k阶矩,应此可以通过样本的k阶矩计算总体的k阶矩。
2)极大似然估计
极大似然估计:


线性代数(新视角)
1)重新看待Ax=b
对于如下矩阵

行视图(凸优化中的超平面)
2x-y=1
x+y=5
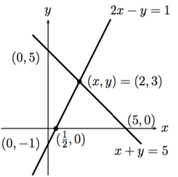
它的解是(x,y)=(2,3)
列视图(矩阵列的线性组合)


2)线性相关与线性无关
对于一个矩阵,使用一组非全为0的系数,如果任一列可以使用其他列线性表出,那么就称这组矩阵是线性相关的,否则非相关。



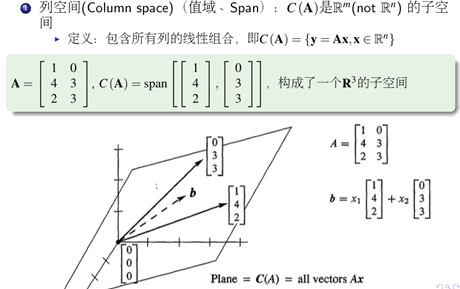
3)Span,基和子空间

对于下面一个问题,S表示为三维空间中的一个平面,如果任意一个线性无关的矩阵可以将S表示出来,那么这个矩阵就可以称为S的一组基。

4)四个基本的子空间
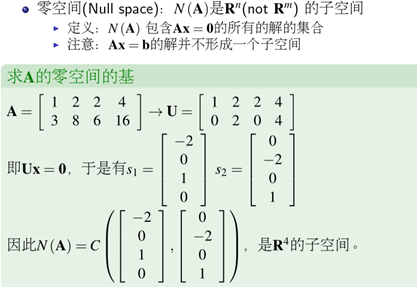

5)四个基本的子空间关系图
对于Ax=b, A的维度是m*n
(1)列空间和零空间,
对于Ax=b ,A的列构成的所有线性组合,构成了列空间,维度是r, 是Rn空间中的一个子空间
Ax=0所有解的的集合构成了零空间,维度是n-r,是Rn空间中的一个子空间,列空间和零空间构成了一个完整的Rn空间
(2)行空间和左零空间
对于ATx=b, A的行构成的所有线性组合,构成了行空间,维度是r, 是Rm空间中的一个子空间
ATy=0所有解的的集合构成了左零空间,维度是m-r,是Rm空间中的一个子空间,行空间和左零空间构成了一个完整的Rm空间。

利用子空间重新看待线性方程组的解:

特征分解
1)一般矩阵
特征分解的一般性质:
已知线性无关的向量,一定存在矩阵的逆。

Tip:并非所有的方阵(n×n)都可以被对角化。
2)对称矩阵
性质1:如果一个对称矩阵的特征值都不相同,则其相应的特征向量不仅线性无关,而且所有的特征向量正交(乘积为0)。
性质2:对称矩阵的特征值都是实数。
性质3:

性质4:

性质5:
对称矩阵可以被U相似对角化(U是特征向量矩阵)
A=UT
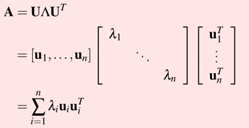
二次型
正定矩阵和负定矩阵均值涉及对称矩阵的,二次型涉及的矩阵是方阵即可。

性质1:对于一个正定矩阵,他的特征值均大于0
特征分解的应用
1)PCA(特征分解)
矩阵A(m×n)的协方差矩阵是一个对称矩阵,根据对称矩阵可以被U相似对角化,则A=UΛUT(U是特征向量矩阵,Λ是对角为方差的对角矩阵)。
降维:
我们取最大的N个特征值对应的特征向量组成的矩阵,可以称之为压缩矩阵;得到了压缩矩阵之后,将去均值的数据矩阵乘以压缩矩阵,就实现了将原始数据特征转化为新的空间特征,进而使数据特征得到了压缩处理。
2)SVD(特征分解的广义化)

SVD和特征分解的关系:

如何计算SVD分解后U,V呢?
我们将A的转置和A做矩阵乘法,那么会得到n×n的一个方阵ATA。既然ATA是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:(ATA)vi=λivi。这样我们就可以得到矩阵ATA的n个特征值和对应的n个特征向量v了。将ATA的所有特征向量张成一个n×n的矩阵V,就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。
反过来我们将A和A的转置做矩阵乘法,将AAT的所有特征向量张成一个m×m的矩阵V,就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。
同时我们可以得到特征值矩阵等于奇异值矩阵的平方。
如何使用SVD进行降维呢?
注意到PCA仅仅使用了我们SVD的右奇异矩阵,没有使用左奇异矩阵,那么左奇异矩阵有什么用呢?
假设我们的样本是m×n的矩阵X,如果我们通过SVD找到了矩阵XXT最大的d个特征向量张成的m×d维矩阵U,则我们如果进行如下处理:
Xd×n′=Ud×mTXm×n
可以得到一个d×n的矩阵X′,这个矩阵和我们原来的m×n维样本矩阵X相比,行数从m减到了k,可见对行数进行了压缩。也就是说,左奇异矩阵可以用于行数的压缩。相对的,右奇异矩阵可以用于列数即特征维度的压缩,也就是我们的PCA降维。
凸优化
1、无约束优化问题
1)为什么要做优化问题?

2)如何优化?
方法一:无约束优化直接分析法

泰勒级数展开(标量):

泰勒级数展开(矢量):

无约束优化直接分析法的缺陷:
1、可能这个函数就不可导
2、函数可以求导,但是变量很多,求不出导数为0的x
3、就算求出了解,但是这个解可能是个集合
方法二:无约束优化迭代法
无约束优化迭代法的基本结构

无约束优化迭代的方法:
第一种:梯度下降法,沿负梯度方向,只使用了一阶导数:搜索比较慢,等值线上显示为Z型走法,轨迹是相互正交的。
第二种:牛顿法。在一阶导数的基础上考虑了二阶导数,性能会更好一点。涉及到了海森矩阵求逆,可能不可逆,比如半正定或者半负定,要做适当修正。等值线上走的是直的。
第三种:拟牛顿法。使用梯度信息去生成对于海森逆矩阵的连续低秩估计。收敛速度比牛顿法相当,但是计算复杂度低很多。
2、有约束优化问题
1)凸集
凸集:简单理解为集合中任意的两个点的连线,均在集合内。

2)凸函数

凸函数判定的两个方法:
方法一:一阶充要条件

方法二:二阶充要条件

总结:
这两种判别方法在判别一个问题是否为凸问题时,往往不能有效的得到结果,因为对于某些问题,他们的一阶导和二阶导并不好求,因此便引出了我们的凸优化问题
2)凸优化问题
(1)概述
如果一个实际的问题可以被表示成凸优化问题,那么我们就可以认为其能够得到很好的解决。常用的解决凸问题的算法有等式优化、内点法等。
对于一个实际问题,如果不能确定其是否为凸函数,便涉及到本章的凸优化的一些方法,比如KKT条件,对偶法等。
如果这个问题是凸问题,那么这些方法解出的极值点就是全局的极值点,如果这个问题不是凸问题,那么这些方法解出的极值点很可能是局部极小点。
(2)KKT条件
KKT条件的基本思想是如何将约束优化问题转化为无约束优化问题。
