逻辑回归-Logistic Regression

因为我们假设样本服从伯努利分布，所以y=1的概率为p，y=0的概率为1-p(y表示样本的类别). 如果用之前的线性回归y=wx(w,x都为向量)直接去拟合样本的话，y值的范围为R, 而概率的取值范围为[0,1]。显然这样是不合理的，概率不可能大于1或小于0. 所以在这里就引入了logit函数. logit函数的定义域为(0,1), 值域为R。所以logit函数可以将p的值映射到R，这样就可以和线性回归建立关系。
                    $odd=\frac{p}{1-p}$
               $logit(odd)=log(odd)=ln(\frac{p}{1-p})$
                    $ln(\frac{p}{1-p})=wx$
在这里取logit(odd)函数的反函数，就可以得到：
                    $p=\frac{1}{1+e^{-wx}}$

这个就是下面的sigmoid函数。

假设函数 :

           $h_\theta(x)=g(\theta^Tx)$
           $g(z)=\frac{1}{1+e^{-z}}$
           $z=\theta^Tx$
逻辑回归在这里引入了sigmoid函数 $g(z)$，可以把回归的结果压缩到[0, 1]的范围。
下图为sigmoid函数的图像：

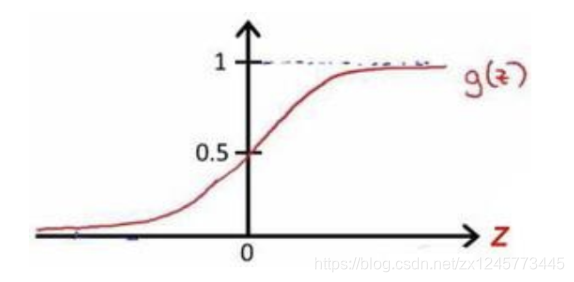
然后选择一个阈值，一般我们选择0.5作为阈值，此时就可以将样本分为两类：
当 $h_\theta(x)>= 0.5$时， y = 1，
当 $h_\theta(x) < 0.5$时，y = 0
所以 $h_\theta(x)$输出结果代表的意思就是样本属于y = 1类的概率，即 $p(y=1|x,\theta)$。因为当 $h_\theta(x)$输出的结果小于0.5时，样本就属于y=0类，也就是说样本属于y=1的概率很小。

决策边界
决策边界是将两类分开的函数, 也就是逻辑回归里面的 $z$. 从前面我们知道
   $g(z)>=0.5$, y = 1;
   $g(z)<0.5$, y = 0
再结合sigmoid函数的图像我们可以看到当 $z>=0$时，就有 $g(z)>=0.5$，即样本的类型y = 1; 当 $z<0$时，就有 $g(z)<0.5$，即样本的类型y = 0，所以函数 $z$就是那条边界。
在这里引用吴恩达的两个例子：
1、linear boundary
假设 $h_\theta(x) =g(-3+x_1+x_2)$， $z=-3+x_1+x_2$
当 $z>=0时$，即 $x_1+x_2>=3$是，y=1
当 $z<0时$，即 $x_1+x_2<3$是，y=0
可视化的结果如下图所示，中间紫色的直线就是决策边界z。边界的右边为y=1的区域，左边为y=0的区域，将两类分割开：

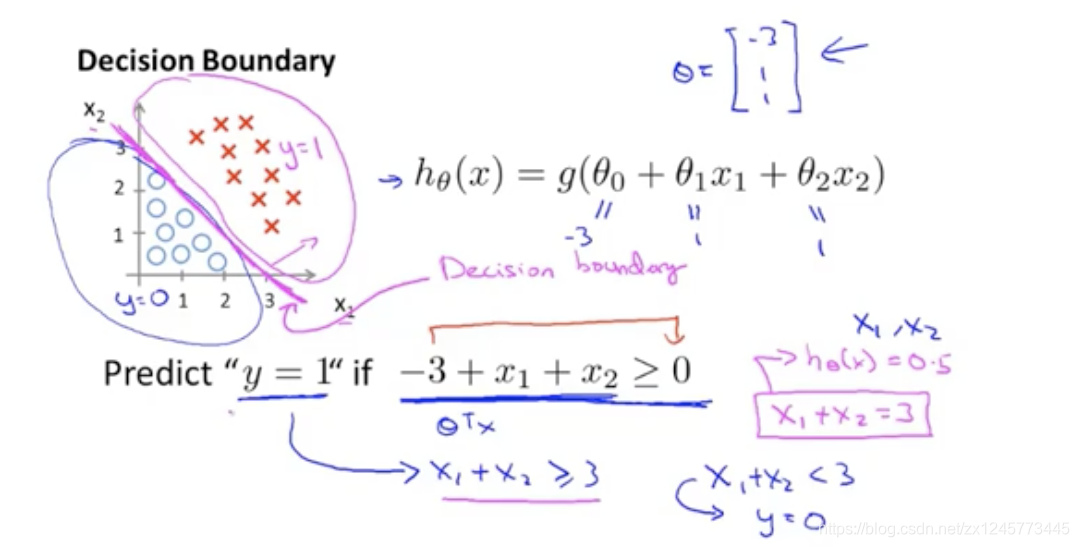
2、non-liner boundary
当两类线性不可分时，可以采用高阶多项式。
假设 $h_\theta(x) =g(-1+x_1^2+x_2^2)$， $z=-1+x_1^2+x_2^2$
当 $z>=0时$，即 $x_1^2+x_2^2>=1$是，y=1
当 $z<0时$，即 $x_1^2+x_2^2<1$是，y=0
可视化的结果如下图所示，中间紫色的圆圈就是决策边界z。边界的外边为y=1的区域，里面为y=0的区域，将两类分割开：

代价函数
代价函数衡量了模型输出的结果和真实值之间的差距。逻辑回归的代价函数可以用极大似然函数给出。 这里没有给出推到过程。

        $J(\theta)=\frac{1}{m}\sum\limits_{i=1}^m{Cost(h_\theta(x_i),y)}$
      

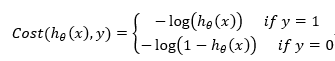
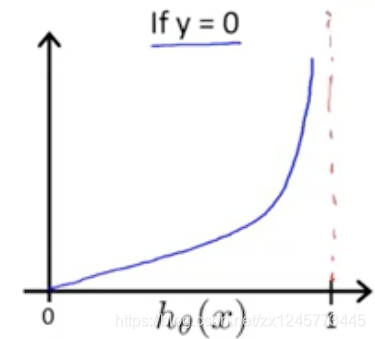
为了简化代价函数的表达式，将代价函数改为：

这样就能保证代价函数为凸函数，所以逻辑回归在最小化代价函数的时候能够获得全局最小值。最后用优化算法，比如梯度下降求解出参数就得到了逻辑回归模型。

参考链接吴恩达的课程：https://study.163.com/course/courseLearn.htm?courseId=1004570029#/learn/video?lessonId=1051024622&courseId=1004570029