今天要写的博客说简单也简单,是大家熟悉的线性模型,但是我们通过线性模型的不足,我们导出岭回归,下面是博客的结构。
1.线性模型
2.线性模型出现的问题
3.改进线性模型—->岭回归的导入
1.线性模型
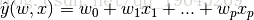
上面的公式是大家再熟悉不过的公式了,通过优化损失函数
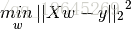
从而可以得到参数w的值。实际上上面优化的公式就相当于求解
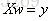
2.线性模型出现的问题
2.1 出现的问题
你有没有考虑过一个问题,当你选取的特征如果存在共线性,或者逼近存在共线性的时候,会出现什么情况呢?
问题:普通的线性模型对噪声非常的敏感
2.2 噪声敏感的例子
给大家举个例子什么叫对噪声比较敏感。
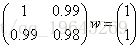
通过求解方程Aw=y可以很容易得到解
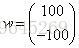
下面给X和y都加点噪声,对系数举证加个扰动,然后对右端项加扰动得到方程
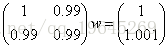
看到没有,只是将X和y加了一点点噪声,和之前的方程变化并不大,但是最后的解会让你大吃一惊。
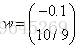
从而可以看出来普通的线性模型对于模型非常的敏感。
这里面实际上牵扯到的是矩阵论中非常重要的一章的内容那就是对矩阵扰动的分析。那么怎么样去判断一个矩阵对噪声是不是很敏感呢,下面通过一个简单的推导,如果想具体看推导的过程可以参照戴华老师的矩阵论。
下面假设只对y进行很小的扰动
定理:
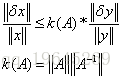
对y进行小小的扰动,不等式左侧表示的是x经过y扰动后的变化情况,从不等式可以看出,当k(A)非常的时候表示,对噪声越明显。
那么为什么上面的情况k(A)非常的大呢。
假设我们用无穷范数来进行衡量k(A),那么上面的例子中,
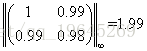

从而可以求出k(A)=3.96*10^4,可以看出k(A)非常的大,所以对噪声特别的敏感。
那么怎么样对A进行处理,使k(A)变小呢?
2.2 解决方式
上面讲到k(A)非常的大:对扰动非常的敏感,可以通过对A加上一个
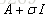
通过上方式可以降低k(A)的值
验证:假设对上面的问题通过加上0.001E得到

从而可以算出

可以得到k(A+0.001I) = 2.089*10^3,可以看出k(A)明显降低,当然如果将系数加大,那么敏感度会进一步降低。
3. 改进线性模型—->岭回归的导入
那么上面扯了那么多,和岭回归有毛关系呢。请看岭回归的损失函数
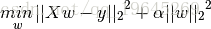
对上面的损失函数对w进行求导
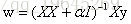
看到没有,这样的处理方式和上面降低敏感度的处理方式是一样的,说明岭回归模型对噪声可以起到鲁棒的作用。
所以岭回归在损失函数后面加上正则化项有以下作用:
A: 使模型简单。
B:对噪声鲁棒