\(\fbox{例30}\)(2017\(\cdot\)广东汕头一模)(求面积的最大值)
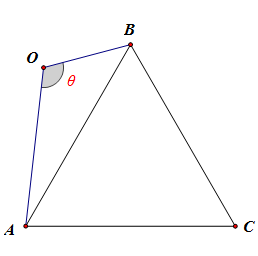
已知\(\Delta ABC\)的内角\(A，B，C\)的对边分别是\(a，b，c\)，且满足\(b=c\)，\(\cfrac{b}{a}=\cfrac{1-cosB}{cosA}\)，若点\(O\)是\(\Delta ABC\)外的一点，\(\angle AOB=\theta(0<\theta<\pi)\)，\(OA=2\)，\(OB=1\)，则四边形\(OACB\)面积的最大值是【】
\(A.\cfrac{4+5\sqrt{3}}{4} \;\; \;\;\) \(B.\cfrac{8+5\sqrt{3}}{4} \;\; \;\;\) \(C.3 \;\; \;\;\) \(D.\cfrac{4+5\sqrt{3}}{4}\)
分析：由\(\cfrac{b}{a}=\cfrac{sinB}{sinA}=\cfrac{1-cosB}{cosA}\)，
得到\(sinBcosA+cosBsinA=sinA\)，即\(sin(A+B)=sinA\)
则\(sinC=sinA\)，即\(A=C\)，
故\(a=b=c\)，为等边三角形。
在\(\Delta AOB\)中，\(AB^2=2^2+1^2-2\cdot 2\cdot 1\cdot cos\theta=5-4cos\theta\)，
故\(S_{OACB}=S_{\Delta AOB}+S_{\Delta ABC}\)
\(=\cfrac{1}{2}\cdot 2\cdot 1\cdot sin\theta+\cfrac{\sqrt{3}}{4}\cdot AB^2\)
\(=sin\theta+\cfrac{\sqrt{3}}{4}(5-4cos\theta)=2sin(\theta-\cfrac{\pi}{3})+\cfrac{5\sqrt{3}}{4}\)
当\(\theta-\cfrac{\pi}{3}=\cfrac{\pi}{2}\)时，即\(\theta=\cfrac{5\pi}{6}\in (0，\pi)\)时，四边形的面积有最大值，
且$S_{max}=2+\cfrac{5\sqrt{3}}{4}=\cfrac{8+5\sqrt{3}}{4} $，故选B。
\(\fbox{例30}\)(2017\(\cdot\)皖北协作区3月联考)(求取值范围)
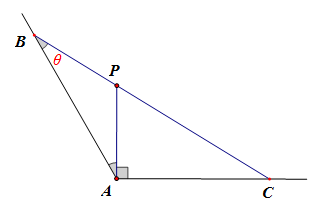
如图，\(\angle BAC=\cfrac{2\pi}{3}\)，\(P\)为\(\angle BAC\)内部一点，过点\(P\)的直线与\(\angle BAC\)的两边交于点\(B、C\)，且\(PA\perp AC\)，\(AP=\sqrt{3}\)。
(1)若\(AB=3\)，求\(PC\)；
分析：在\(\Delta ABP\)中，\(\angle BAP=30^{\circ}\)，\(AB=3\)，\(AP=\sqrt{3}\)，
由余弦定理得到\(BP=\sqrt{3}\)，故\(\angle BAP=\angle PBA=30^{\circ}\)，
则\(\angle APC=60^{\circ}\)，在\(Rt\Delta APC\)中，可得\(PC=2\sqrt{3}\)。
(2)求\(\cfrac{1}{PB}+\cfrac{1}{PC}\)的取值范围。
分析：设\(\angle PBA=\theta\)，则\(\theta\in (0，\cfrac{\pi}{3})\)；
(说明：当过点\(P\)的直线和\(AB\)平行时，\(\theta=0\)；当过点\(P\)的直线和\(AC\)平行时，\(\theta=\cfrac{\pi}{3}\))
在\(\Delta ABP\)中，\(\angle BAP=30^{\circ}\)，\(\angle PBA=\theta\)，\(AP=\sqrt{3}\)，
故由正弦定理得到\(\cfrac{PB}{sin30^{\circ}}=\cfrac{\sqrt{3}}{sin\theta}\)，即\(PB=\cfrac{\cfrac{\sqrt{3}}{2}}{sin\theta}\)；
在\(Rt\Delta APC\)中，\(\angle CPA=\theta+\cfrac{\pi}{6}\)，\(PC=\cfrac{\sqrt{3}}{cos(\theta+\cfrac{\pi}{6})}\)，
故\(\cfrac{1}{PB}+\cfrac{1}{PC}=\cfrac{2sin\theta}{\sqrt{3}}+\cfrac{cos(\theta+\cfrac{\pi}{6})}{\sqrt{3}}\)
\(=\cfrac{1}{\sqrt{3}}(\cfrac{3}{2}sin\theta+\cfrac{\sqrt{3}}{2}cos\theta)\)
\(=sin(\theta+\cfrac{\pi}{6})\)，且\(\theta\in (0，\cfrac{\pi}{3})\)；
故\(\cfrac{1}{2}<sin(\theta+\cfrac{\pi}{6})<1\)。
\(\fbox{例31}\)
函数\(f(x)=2cos(\omega x+\phi)(\omega\neq 0)\)对任意\(x\)都有\(f(\cfrac{\pi}{4}+x)=f(\cfrac{\pi}{4}-x)\)成立，则\(f(\cfrac{\pi}{4})\)的值为【】
A、\(2或0\) \(\hspace{2cm}\) B、\(-2或2\) \(\hspace{2cm}\) C、\(0\) \(\hspace{2cm}\) D、 \(-2或0\)
分析：由任意\(x\)都有\(f(\cfrac{\pi}{4}+x)=f(\cfrac{\pi}{4}-x)\)成立，
可知\(x=\cfrac{\pi}{4}\)为函数的一条对称轴，
而正弦型或余弦型函数在对称轴处必然会取到最值，
故\(f(\cfrac{\pi}{4})=\pm 2\)，选B。
解后反思：此题目如果不注意函数的性质，往往会想到求\(\omega\)和\(\phi\)，这样思路就跑偏了。
\(\fbox{例32}\)
已知\(\cfrac{\pi}{2}<\beta<\alpha<\cfrac{3\pi}{4}\)，\(cos(\alpha-\beta)=\cfrac{12}{13}\)，\(sin(\alpha+\beta)=-\cfrac{3}{5}\)， 则\(sin\alpha+cos\alpha\)的值为_____。
分析：先由给定的不等式求解\(\alpha\pm \beta\)的范围，以便于求解其余名函数的值，为后续的计算打基础。
由\(\cfrac{\pi}{2}<\beta<\alpha<\cfrac{3\pi}{4}\)，
得到\(\cfrac{\pi}{2}<\alpha<\cfrac{3\pi}{4}\)，\(\cfrac{\pi}{2}<\beta<\cfrac{3\pi}{4}\)，
故\(\pi<\alpha+\beta<\cfrac{3\pi}{2}\)，由\(sin(\alpha+\beta)=-\cfrac{3}{5}\)，
得到\(cos(\alpha+\beta)=-\cfrac{4}{5}\)；
又由\(\cfrac{\pi}{2}<\alpha<\cfrac{3\pi}{4}\)，\(-\cfrac{3\pi}{4}<-\beta<-\cfrac{\pi}{2}\)，及\(\alpha-\beta>0\)
得到\(0<\alpha-\beta<\cfrac{\pi}{4}\)，由\(cos(\alpha-\beta)=\cfrac{12}{13}\)，
得到\(sin(\alpha-\beta)=\cfrac{5}{13}\)；
\(sin2\alpha=sin[(\alpha+\beta)+(\alpha-\beta)]\)
\(=sin(\alpha+\beta)cos(\alpha-\beta)+cos(\alpha+\beta)sin(\alpha-\beta)=-\cfrac{56}{65}\)
又\((sin\alpha+cos\alpha)^2=1+sin2\alpha=\cfrac{9}{65}\)
又由于\(\cfrac{\pi}{2}<\beta<\alpha<\cfrac{3\pi}{4}\)，借助三角函数线可知
则有\(sin\alpha+cos\alpha>0\)，
故\(sin\alpha+cos\alpha=\sqrt{\cfrac{9}{65}}=\cfrac{3\sqrt{65}}{65}\)。
\(\fbox{例33}\)【2018高考一卷第16题】
求\(f(x)=2sinx+sin2x\)的最小值。
法1：\(f'(x)=2cosx+2cos2x=2cosx+2(2cos^x-1)\)
\(=4cos^2x+2cosx-2=(2cosx+2)(2cosx-1)\)
\(=4(cosx+1)(cosx-\cfrac{1}{2})\)
注意到\(cosx+1\ge 0\)恒成立，故
令\(f'(x)>0\)得到，\(cosx>\cfrac{1}{2}\)，令\(f'(x)<0\)得到，\(cosx<\cfrac{1}{2}\)，
则\(x\in [2k\pi-\cfrac{5\pi}{3}，2k\pi-\cfrac{\pi}{3}](k\in Z)\)时，函数\(f(x)\)单调递减；
\(x\in [2k\pi-\cfrac{\pi}{3}，2k\pi+\cfrac{\pi}{3}](k\in Z)\)时，函数\(f(x)\)单调递增；
故当\(x=2k\pi-\cfrac{\pi}{3}(k\in Z)\)时，\(f(x)_{min}=f(\cfrac{2k\pi-\pi}{3})=-\cfrac{3\sqrt{3}}{2}\)。
\(\fbox{例34}\)【2019届高三理科数学课时作业用题】
在斜三角形\(ABC\)中，\(sinA=-\sqrt{2}cosBcosC\)，且\(tanBtanC=1-\sqrt{2}\)，则角\(A\)的大小为【】
法1分析：由\(sinA=sin(B+C)=sinBcosC+cosBsinC=-\sqrt{2}cosBcosC\)，
则\(\cfrac{sinBcosC+cosBsinC}{cosBcosC}=tanB+tanC=-\sqrt{2}\)，
又由于\(tanBtanC=1-\sqrt{2}\)，故\(-tanA=tan(B+C)=\cfrac{tanB+tanC}{1-tanBtanC}\)，
即\(-tanA=\cfrac{-\sqrt{2}}{1-(1-\sqrt{2})}=-1\)，故\(tanA=1\)，又\(A\in (0，\pi)\)，
则\(A=\cfrac{\pi}{4}\)，故选\(A\)。