vc维知识:

预备知识:

伯努利分布:即0-1分布.

知识网站:

http://www.flickering.cn/machine_learning/2015/04/vc%E7%BB%B4%E7%9A%84%E6%9D%A5%E9%BE%99%E5%8E%BB%E8%84%89/

上面文章修正:

Shatter的概念：当假设空间H作用于N个input的样本集时，产生的dichotomies数量等于这N个点总的组合数2^N时，就称：这N个inputs被H给shatter掉了。

激活函数:

激励函数的作用:

一个线性神经元就像一个小毛团，每当有东西戳它一下的时候，它就会戳跟着它的毛团一下，就像多米诺骨牌。
但是有时候其实你不需要知道具体被戳了多少下。我们来考虑一个防烫手的机制，假如现在在手指上有一个小神经元A（输入层）可以感知手指附近的温度，它连接到了另一个神经元B（隐藏层），在连接一个用来控制缩回手的神经元C（输出层）。
这个小神经元A感受到环境的温度是x度，然后飞快地戳了身后的神经元Bx下。神经元B接着也戳了Cx下。这时C也不知道要不要收回手，因为只收到了环境的温度。
这时候在神经元B旁边加入一个神经元D（bias），D在每次B要戳C之前会告诉B冷静一下，然后挡住B戳的前n下，表明温度在n度以下时不需要缩手。于是最终C被戳到的次数就是（x-n），如果C被戳到了，说明温度比n度要高，此时就应该要缩手了。
但是被戳了一下和两下也没有区别呀，于是我们用阶跃函数作为激励函数，这样当（x-n）大于零的时候，B就戳C一下就好了，否则就不要戳。C被戳到了就可以缩手了。
所以其实激励函数的作用就是处理输入产生输出～

激活函数的作用就是为了模拟神经刺激,以sigmod函数为例子,当刺激小于某个值的时候,不会有输出,当输入足够大的时候,再增加输入也不会带来更明显的收益,神经网络这个方法的成败完全取决于激励函数,取决于实际问题和神经刺激有多像

神经网络的激励函数（activation function）是一群空间魔法师，扭曲翻转特征空间，在其中寻找线性的边界。

如果没有激励函数，那么神经网络的权重、偏置全是线性的仿射变换

这样的神经网络，甚至连下面这样的简单分类问题都解决不了：

没有激励函数的加持，神经网络最多能做到这个程度：

这时候，激励函数出手了，扭曲翻转一下空间：

线性边界出现了！再还原回去，不就得到了原特征空间中的边界？

当然，不同的激励函数，因为所属流派不同，所以施展的魔法也各不相同。

上图中，出场的三位空间魔法师，分别为sigmoid、tanh、relu

sigmoid

sigmoid是一位老奶奶，是激励函数中最有资历的。

虽然比较老迈、古板，已经不像当年那么受欢迎了，但在分类任务的输出层中，人们还是信赖sigmoid的丰富经验。

我们可以看到，sigmoid将输出挤压进0到1区间（这和概率的取值范围一致），这正是分类任务中sigmoid很受欢迎的原因。它可以想象成一个神经元的放电率，在中间斜率比较大的地方是神经元的敏感区，在两边斜率很平缓的地方是神经元的抑制区。

当然，流行也是曾经流行，这说明函数本身是有一定的缺陷的。

1) 当输入稍微远离了坐标原点，函数的梯度就变得很小了，几乎为零。在神经网络反向传播的过程中，我们都是通过微分的链式法则来计算各个权重w的微分的。当反向传播经过了sigmod函数，这个链条上的微分就很小很小了，况且还可能经过很多个sigmod函数，最后会导致权重w对损失函数几乎没影响，这样不利于权重的优化，这个问题叫做梯度饱和，也可以叫梯度弥散。

2) 函数输出不是以0为中心的，这样会使权重更新效率降低。对于这个缺陷，在斯坦福的课程里面有详细的解释。

3) sigmod函数要进行指数运算，这个对于计算机来说是比较慢的。

tanh

tanh也是一位资深的空间魔法师：

等等，这不就是sigmoid？背过身去以为我们就不认识了吗？

没错，tanh就是乔装打扮的sigmoid：

tanh及其梯度（红色曲线为梯度）

如上图所示，tanh的形状和sigmoid类似，只不过tanh将“挤压”输入至区间(-1, 1)。因此，中心为零，（某种程度上）激活值已经是下一层的正态分布输入了。

至于梯度，它有一个大得多的峰值1.0（同样位于z = 0处），但它下降得更快，当|z|的值到达3时就已经接近零了。这是所谓梯度消失（vanishing gradients）问题背后的原因，会导致网络的训练进展变慢。

ReLU

ReLU是一个守门人，凡是麻瓜（0）一律拒之门外（关闭神经元）。

它是今时今日寻常使用的激励函数。ReLU处理了它的sigmoid、tanh中常见的梯度消失问题，同时也是计算梯度最快的激励函数。

ReLU(Rectified Linear Unit)函数是目前比较火的一个激活函数，相比于sigmod函数和tanh函数，它有以下几个优点：

1) 在输入为正数的时候，不存在梯度饱和问题。

2) 计算速度要快很多。ReLU函数只有线性关系，不管是前向传播还是反向传播，都比sigmod和tanh要快很多。（sigmod和tanh要计算指数，计算速度会比较慢）

当然，缺点也是有的：

1) 当输入是负数的时候，ReLU是完全不被激活的，这就表明一旦输入到了负数，ReLU就会死掉。这样在前向传播过程中，还不算什么问题，有的区域是敏感的，有的是不敏感的。但是到了反向传播过程中，输入负数，梯度就会完全到0，这个和sigmod函数、tanh函数有一样的问题。

2) 我们发现ReLU函数的输出要么是0，要么是正数，这也就是说，ReLU函数也不是以0为中心的函数。

ELU函数

ELU函数公式和曲线如下图

ELU函数是针对ReLU函数的一个改进型，相比于ReLU函数，在输入为负数的情况下，是有一定的输出的，而且这部分输出还具有一定的抗干扰能力。这样可以消除ReLU死掉的问题，不过还是有梯度饱和和指数运算的问题。

PReLU函数

PReLU也是针对ReLU的一个改进型，在负数区域内，PReLU有一个很小的斜率，这样也可以避免ReLU死掉的问题。相比于ELU，PReLU在负数区域内是线性运算，斜率虽然小，但是不会趋于0，这算是一定的优势吧。

我们看PReLU的公式，里面的参数α一般是取0~1之间的数，而且一般还是比较小的，如零点零几。当α=0.01时，我们叫PReLU为Leaky ReLU，算是PReLU的一种特殊情况吧。

BP算法:

BP的目的

首先我们要搞清楚两个问题

为什么要求梯度？
求关于谁的梯度？

上图展示了一个神经网络。神经网络可以看作是一个函数 $y=f_w(x)$ ， $x$ 是输入， $y$ 是输出， $w$ 是 $f$ 的参数。 $w$ 的真实值是我们的目标，但我们有的只是一些 $x$ 和与之对应的真实的 $y=f(x)$ 的值，所以我们要用到这两个值去估计 $w$ 的真实值。这个问题可以看成下面的优化问题（优化问题即求函数最小值）

其中我们令 $E=\sum_x||f_w(x) - y||^2$ ，并称之为误差项。我们的目标就是求一组 $w$ 使得 $E$ 最小。求解这类问题有个经典的方法叫做梯度下降法（SGD, Stochastic Gradient Descent），这个算法一开始先随机生成一个 $w$ ，然后用下面的公式不断更新 $w$ 的值，最终能够逼近真实结果。

其中 $\frac{\partial E}{\partial w}$ 是当前的误差 $E$ 关于 $w$ 的梯度，它的物理意义是当 $w$ 变化的时候 $E$ 随之变化的幅度， $\eta$ 叫做学习率，通常在 $0.1$ 以下，用来控制更新的步长（防止步子太大扯到蛋哈哈）。所以，开头的两个问题答案就有了：求梯度的原因是我们需要它来估算真实的 $w$ ，求的是误差项 $E$ 关于参数 $w$ 的梯度。

链式法则--BP的基础

在正式推导BP之前，我们首先需要回忆一下求导数的链式法则，这个是BP的基础和核心。假设 $y = g(x), z = f(y)$ ，那么 $z = h(x), h = f\circ g$ 。我们知道 $\frac{dy}{dx} = g'(x), \frac{dz}{dy}=f'(y)$ ，那么如何求 $z$ 对 $x$ 的导数 $\frac{dz}{dx}$ 呢？这个时候链式法则就出场了，根据微积分的知识 $h'(x) = \frac{dz}{dx} = \frac{dz}{dy}\cdot \frac{dy}{dx}$ ，即复合函数的求导可以使用乘法法则，也称为链式法则，待会儿我们会用到。上面给出的是单变量的情况，多变量同样适用。

Back Propagation By Example

现在我们用一个例子来讲解BP，如下图所示，我们选取的例子是最简单的feed forward neural network，它有两层，输入层有两个神经元 $x_1,x_2$ ，隐藏层有两个神经元 $h_1,h_2$ ，最终输出只有一个神经元 $y$ ，各个神经元之间全连接。为了直观起见，我们给各个参数赋上具体的数值。我们令 $x_1 = 1, x_2 = 0.5$ ，然后我们令 $w_1,w_2,w_3,w_4$ 的真实值分别是 $1,2,3,4$ ，令 $w_5,w_6$ 的真实值是 $0.5,0.6$ 。这样我们可以算出 $y$ 的真实目标值是 $t=4$ 。

那么为了模拟一个Back Propagation的过程，我们假设我们只知道 $x_1 = 1, x_2 = 0.5$ ，以及对应的目标 $t=4$ 。我们不知道 $w_1,w_2,w_3,w_4,w_5,w_6$ 的真实值，现在我们需要随机为他们初始化值，假设我们的随机化结果是 $w_1 = 0.5, w_2 = 1.5, w_3 = 2.3, w_4 = 3, w_5=1,w_6=1$ 。下面我们就开始来一步步进行Back Propagation吧。

首先，在计算反向传播之前我们需要计算Feed Forward Pass，也即是预测的 $h_1,h_2,y$ 和误差项 $E$ ，其中 $E = \frac{1}{2}(t - y)^2$ 。根据网络结构示意图，各个变量的计算公式为：

$\begin{align} h_1 & = w_1 \cdot x_1 + w_2 \cdot x_2 = 1.25\\ h_2 & = w_3\cdot x_1 + w_4\cdot x_2 = 3.8 \\ y & = w_5\cdot h_1 + w_6\cdot h_2 = 5.05 \\ E & = \frac{1}{2}(y - t)^2 = 0.55125 \end{align}\\$

现在Feed Forward Pass算完了，我们来计算Backward Pass。 $y$ 是神经网络预测的值，真实的输出是 $t = 4$ 。那么，要更新 $w_5$ 的值我们就要算 $\frac{\partial E}{\partial w_5}$ ，根据链式法则有

$\frac{\partial E}{\partial w_5} = \frac{\partial E}{\partial y}\cdot \frac{\partial y}{\partial w_5}\\$

因为 $E= \frac{1}{2}(t-y)^2$ ，所以

$\begin{align} \frac{\partial E}{\partial y} & = 2\cdot \frac{1}{2}\cdot(t-y)\cdot(-1)\\ &=y - t \\ & = 5.05 - 4 = 1.05 \end{align}\\$

而 $y = w_5 * h1 + w_6*h2$ ，所以

$\frac{\partial y}{\partial w_5} = h_1 + 0 = h_1 = 1.25\\$

把上面两项相乘我们得到

$\begin{align} \frac{\partial E}{\partial w_5} & = \frac{\partial E}{\partial y}\cdot \frac{\partial y}{\partial w_5} = (y-t)\cdot h_1\\ & = 1.05\cdot 1.25 = 1.3125 \end{align}\\$

运用之前梯度下降法的公式更新 $w_5$ ，得到新的 $w_5^+$ 。其中我们假设 $\eta = 0.1$ （并且后面所有的 $\eta$ 都等于 $0.1$ ）

$\begin{align} w^+_5 & = w_5 - \eta\cdot \frac{\partial E}{\partial w_5}\\ & = 1 - 0.1\cdot 1.3125\\ & = 0.86875 \end{align}\\$

同理，我们可以按照相同的步骤计算 $w_6^+$ 的更新公式

$\begin{align} w^+_6 & = w_6 - \eta\cdot \frac{\partial E}{\partial w_6}\\ & = 1 - 0.1\cdot 3.99 \\ & = 0.601 \end{align}\\$

下面我们再来看 $w_1,w_2,w_3,w_4$ ，由于这四个参数在同一层，所以求梯度的方法是相同的，因此我们这里仅展示对 $w_1$ 的推导。根据链式法则

$\frac{\partial E}{\partial w_1} = \frac{\partial E}{\partial y}\cdot \frac{\partial y}{\partial h_1}\cdot \frac{\partial h_1}{\partial w_1}\\$

其中 $\frac{\partial E}{\partial y} = y - t$ 在求 $\frac{\partial E}{\partial w_5}$ 的时候已经求过了。而根据 $y = w_5 \cdot h_1 + w_6\cdot h_2$ 我们可以得到

$\frac{\partial y}{\partial h_1} = w_5 + 0 = w_5\\$

又根据 $h_1 = w_1\cdot x_1+w_2\cdot x_2$ 我们可以得到

$\frac{\partial h_1}{\partial w_1} = x_1 + 0 = x_1\\$

因此我们有下面的公式

$\frac{\partial E}{\partial w_1} = (y-t) \cdot w_5 \cdot x_1\\$

现在我们代入数字并使用梯度下降法更新 $w_1$

$\begin{align} w_1^+ & = w_1 - \eta\cdot \frac{\partial E}{\partial w_1}\\ & = w_1 - \eta\cdot (y-t) \cdot w_5 \cdot x_1\\ & = 0.5 - 0.1 \cdot 1.05\cdot 1 \cdot 1 \\ & = 0.395 \end{align}\\$

然后重复这个步骤更新 $w_2,w_3,w_4$

$\begin{align} w_2^+ & = w_2 - \eta\cdot \frac{\partial E}{\partial w_2}\\ & = w_2 - \eta\cdot (y-t) \cdot w_5 \cdot x_2\\ & = 1.5 - 0.1\cdot 1.05\cdot 1 \cdot 0.5 \\ & = 1.4475 \end{align}\\$

$\begin{align} w_3^+ & = w_3 - \eta\cdot \frac{\partial E}{\partial w_3}\\ & = w_3 - \eta\cdot (y-t) \cdot w_6 \cdot x_1\\ & = 2.3 - 0.1\cdot 1.05\cdot 1 \cdot 1 \\ & = 2.195 \end{align}\\$

$\begin{align} w_4^+ & = w_4 - \eta\cdot \frac{\partial E}{\partial w_4}\\ & = w_2 - \eta\cdot (y-t) \cdot w_5 \cdot x_2\\ & = 3 - 0.1\cdot 1.05\cdot 1 \cdot 0.5 \\ & = 2.9475 \end{align}\\$

Great！现在我们已经更新了所有的梯度，完成了一次梯度下降法。我们用得到的新的 $w^+$ 再来预测一次网络输出值，根据Feed Forward Pass得到 $y^+= 3.1768$ ，那么新的误差是 $E^+=0.3388$ ，相比于之前的 $E=0.55125$ 确实是下降了呢，说明我们的模型预测稍微准了一点。只要重复这个步骤，不断更新网络参数我们就能学习到更准确的模型啦。

另一篇关于bp实例的讲解:https://zhuanlan.zhihu.com/p/24801814

可以参考的原理:以数学推导为主---->https://blog.csdn.net/u014303046/article/details/78200010

softmax函数:

softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！

假设我们有一个数组，V，Vi表示V中的第i个元素，那么这个元素的softmax值就是

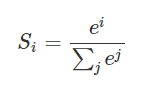
更形象的如下图表示：

softmax直白来说就是将原来输出是3,1,-3通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标！

举一个我最近碰到利用softmax的例子：我现在要实现基于神经网络的句法分析器。用到是基于转移系统来做，那么神经网络的用途就是帮我预测我这一个状态将要进行的动作是什么？比如有10个输出神经元，那么就有10个动作，1动作，2动作，3动作...一直到10动作。（这里涉及到nlp的知识，大家不用管，只要知道我现在根据每个状态（输入），来预测动作（得到概率最大的输出），最终得到的一系列动作序列就可以完成我的任务即可）

原理图如下图所示：

那么比如在一次的输出过程中输出结点的值是如下：

[0.2,0.1,0.05,0.1,0.2,0.02,0.08,0.01,0.01,0.23]

那么我们就知道这次我选取的动作是动作10，因为0.23是这次概率最大的，那么怎么理解多分类呢？很容易，如果你想选取俩个动作，那么就找概率最大的俩个值即可~（这里只是简单的告诉大家softmax在实际问题中一般怎么应用）

二、softmax相关求导

当我们对分类的Loss进行改进的时候，我们要通过梯度下降，每次优化一个step大小的梯度，这个时候我们就要求Loss对每个权重矩阵的偏导，然后应用链式法则。那么这个过程的第一步，就是对softmax求导传回去，不用着急，我后面会举例子非常详细的说明。在这个过程中，你会发现用了softmax函数之后，梯度求导过程非常非常方便！

下面我们举出一个简单例子，原理一样，目的是为了帮助大家容易理解！

我们能得到下面公式：

z4 = w41*o1+w42*o2+w43*o3

z5 = w51*o1+w52*o2+w53*o3

z6 = w61*o1+w62*o2+w63*o3

z4,z5,z6分别代表结点4,5,6的输出，01,02,03代表是结点1,2,3往后传的输入.

那么我们可以经过softmax函数得到

$a_{4}= \frac{e^{z4} }{z^{z4}+z^{z5}+z^{z6}}$

$a_{5} =\frac{e^{z5} }{z^{z4}+z^{z5}+z^{z6}}$ $a_{6}= \frac{e^{z6} }{z^{z4}+z^{z5}+z^{z6}}$

上面式子底数的z换成a

好了，我们的重头戏来了，怎么根据求梯度，然后利用梯度下降方法更新梯度！

要使用梯度下降，肯定需要一个损失函数，这里我们使用交叉熵作为我们的损失函数，为什么使用交叉熵损失函数，不是这篇文章重点，后面有时间会单独写一下为什么要用到交叉熵函数（这里我们默认选取它作为损失函数）

交叉熵函数形式如下：

$Loss = -\sum_{i}^{}{y_{i}lna_{i} }$

其中y代表我们的真实值，a代表我们softmax求出的值。i代表的是输出结点的标号！在上面例子，i就可以取值为4,5,6三个结点（当然我这里只是为了简单，真实应用中可能有很多结点）

现在看起来是不是感觉复杂了，居然还有累和，然后还要求导，每一个a都是softmax之后的形式！

但是实际上不是这样的，我们往往在真实中，如果只预测一个结果，那么在目标中只有一个结点的值为1，比如我认为在该状态下，我想要输出的是第四个动作（第四个结点）,那么训练数据的输出就是a4 = 1,a5=0,a6=0，哎呀，这太好了，除了一个为1，其它都是0，那么所谓的求和符合，就是一个幌子，我可以去掉啦！

为了形式化说明，我这里认为训练数据的真实输出为第j个为1，其它均为0！

那么Loss就变成了 $Loss = -y_{j}lna_{j}$ ,累和已经去掉了，太好了。现在我们要开始求导数了！

我们在整理一下上面公式，为了更加明白的看出相关变量的关系：

其中 $y_{j} =1$ ,那么形式变为 $Loss = -lna_{j}$

那么形式越来越简单了，求导分析如下：

参数的形式在该例子中，总共分为w41,w42,w43,w51,w52,w53,w61,w62,w63.这些，那么比如我要求出w41,w42,w43的偏导，就需要将Loss函数求偏导传到结点4，然后再利用链式法则继续求导即可，举个例子此时求w41的偏导为:

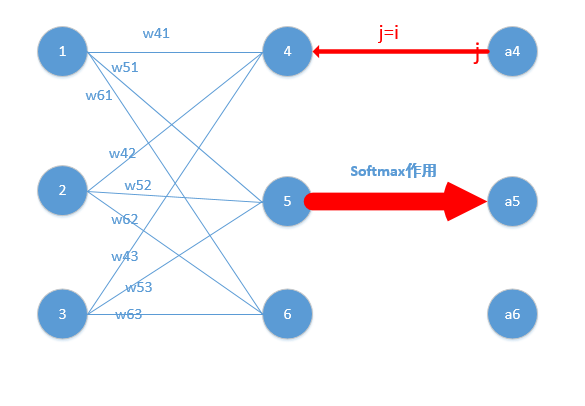
w51.....w63等参数的偏导同理可以求出，那么我们的关键就在于Loss函数对于结点4,5,6的偏导怎么求，如下：

这里分为俩种情况：

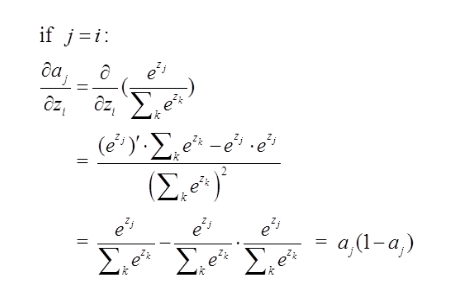
j=i对应例子里就是如下图所示：

比如我选定了j为4，那么就是说我现在求导传到4结点这！

那么由上面求导结果再乘以交叉熵损失函数求导

$Loss = -lna_{j}$ ，它的导数为 $-\frac{1}{a_{j} }$ ,与上面 $a_{j}(1-a_{j} )$ 相乘为 $a_{j}-1$ （形式非常简单，这说明我只要正向求一次得出结果，然后反向传梯度的时候，只需要将它结果减1即可，后面还会举例子！）那么我们可以得到Loss对于4结点的偏导就求出了了（这里假定4是我们的预计输出）

第二种情况为：

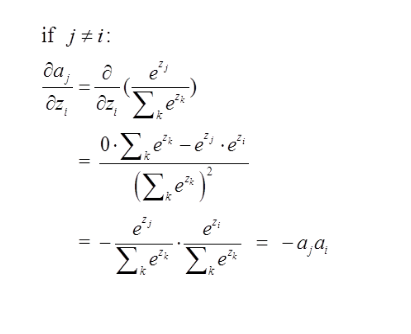
这里对应我的例子图如下，我这时对的是j不等于i，往前传：

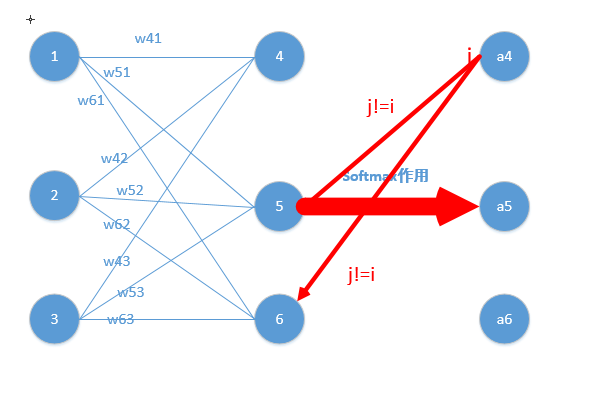
那么由上面求导结果再乘以交叉熵损失函数求导

$Loss = -lna_{j}$ ，它的导数为 $-\frac{1}{a_{j} }$ ,与上面 $-a_{j}a_{i}$ 相乘为 $a_{i}$ （形式非常简单，这说明我只要正向求一次得出结果，然后反向传梯度的时候，只需要将它结果保存即可，后续例子会讲到）这里就求出了除4之外的其它所有结点的偏导，然后利用链式法则继续传递过去即可！我们的问题也就解决了！

三、下面我举个例子来说明为什么计算会比较方便，给大家一个直观的理解

举个例子，通过若干层的计算，最后得到的某个训练样本的向量的分数是[ 2, 3, 4 ],
那么经过softmax函数作用后概率分别就是=[ $\frac{e^{2} }{e^{2}+e^{3}+e^{4}}$
, $\frac{e^{3} }{e^{2}+e^{3}+e^{4}}$ , $\frac{e^{4} }{e^{2}+e^{3}+e^{4}}$ ] = [0.0903,0.2447,0.665],如果这个样本正确的分类是第二个的话，那么计算出来的偏导就是[0.0903,0.2447-1,0.665]=[0.0903,-0.7553,0.665]，是不是非常简单！！然后再根据这个进行back propagation就可以了