利用Numpy的svd函数实现的PCA为什么是对协方差矩阵进行SVD分解

众所周知，PCA是数据分析中经常用到的一种方法，主要用途是对高维数据进行降维，有两大目的：去相关和去冗余。

其大致的原理是通过对数据协方差矩阵进行特征分解找到使数据各维度方差最大的主成分，并将原数据投影到各主成分上达到去相关的目的，若在投影到各主成分时，仅选取特征值最大的前若干个主成分，则可同时实现去冗余的目的。
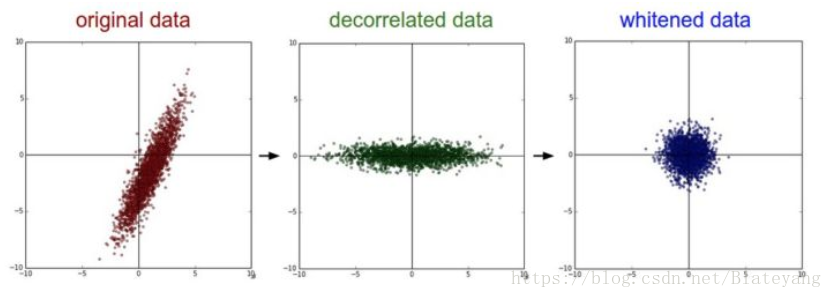
这里写图片描述
上图的decorrelate data就是对原数据进行PCA去相关后的效果，其中x方向是第一主成分，y方向是第二主成分。

PCA的主要算法如下：

组织数据形式，以便于模型使用；
计算样本每个特征的平均值；
每个样本数据减去该特征的平均值（归一化处理）；
求协方差矩阵；
找到协方差矩阵的特征值和特征向量；
对特征值和特征向量重新排列（特征值从大到小排列）；
对特征值求取累计贡献率或指定选取前若干个特征向量（跳过8）；
对累计贡献率按照某个特定比例选取特征向量集的子集合；
对原始数据（第三步后）进行转换。

关于PCA的原理和推导网上有很多资料，比如主成分分析(PCA)原理详解，博主在此想要讨论的主要有两点：
1. 为什么PCA选择处理的对象是协方差矩阵？
2. 为什么用numpy的svd函数实现PCA要对协方差矩阵进行SVD分解？

对于第一个问题，即为什么PCA选择处理的对象是协方差矩阵？
引用博客PCA为什么要用协方差矩阵中的话

降维的目的就是“降噪”和“去冗余”。“降噪”的目的就是使保留下来的维度间的相关性尽可能小，而“去冗余”的目的就是使保留下来的维度含有的“能量”即方差尽可能大。那首先的首先，我们得需要知道各维度间的相关性以及个维度上的方差啊！那有什么数据结构能同时表现不同维度间的相关性以及各个维度上的方差呢？自然是协方差矩阵！
协方差矩阵度量的是维度与维度之间的关系，而非样本与样本之间。协方差矩阵的主对角线上的元素是各个维度上的方差(即能量)，其他元素是两两维度间的协方差(即相关性)。我们要的东西协方差矩阵都有了。

对于第二个问题，为什么用numpy的svd函数实现PCA要对协方差矩阵进行SVD分解？
其实实现PCA有多种方法，博主找到的至少有三种：
1. 直接对原数据矩阵进行SVD分解(sklearn中用的是这一种）
2. 基于协方差矩阵进行特征分解（上面的算法描述的就是这一种）
3. 基于协方差矩阵进行SVD分解（本问题指的是这一种）
前两种实现方法比较容易理解，博主认为它们实际也是等价的，因为线性代数中对矩阵X进行SVD的分解过程其实就用到了对协方差矩阵 $X^TX$ 的特征分解，矩阵X的奇异值 $\sigma_i$ 就是协方差矩阵的特征值 $\sigma_i^2$ 的平方根。
而第三种实现方法，就有些费解，明明对协方差矩阵用特征分解就可以了，为什么又可以用SVD分解。搜了一通资料后才知道SVD分解也是可以用来做特征分解的，而且它比特征分解的适用范围更广，特征分解只能用于方阵，而SVD分解可用于任意m*n形状的矩阵。另外，如果我们通过特征值分解协方差矩阵，那么我们只能得到一个方向的PCA降维。这个方向就是对数据矩阵X从行-对 $XX^T$ 进行特征分解的情况(或列-对 $X^TX$ 进行特征分解的情况)方向上压缩降维。而用SVD对协方差矩阵进行特征分解，可以得到两个方向上的PCA降维（即行和列方向，只要用SVD分解得到的U或V分别去和X相乘即可，注意维度匹配）

下面附上以上三种实现的python代码

import numpy as np
from sklearn.decomposition import PCA
import sys
#returns choosing how many main factors
def index_lst(lst, component=0, rate=0):
    #component: numbers of main factors
    #rate: rate of sum(main factors)/sum(all factors)
    #rate range suggest: (0.8,1)
    #if you choose rate parameter, return index = 0 or less than len(lst)
    if component and rate:
        print('Component and rate must choose only one!')
        sys.exit(0)
    if not component and not rate:
        print('Invalid parameter for numbers of components!')
        sys.exit(0)
    elif component:
        print('Choosing by component, components are %s......'%component)
        return component
    else:
        print('Choosing by rate, rate is %s ......'%rate)
        for i in range(1, len(lst)):
            if sum(lst[:i])/sum(lst) >= rate:
                return i
        return 0

def main():
    # test data
    mat = [[-1,-1,0,2,1],[2,0,0,-1,-1],[2,0,1,1,0]]

    # simple transform of test data
    Mat = np.array(mat, dtype='float64')
    print('Before PCA transforMation, data is:\n', Mat)
    print('\nMethod 1: PCA by original algorithm:')
    p,n = np.shape(Mat) # shape of Mat 
    t = np.mean(Mat, 0) # mean of each column

    # substract the mean of each column
    for i in range(p):
        for j in range(n):
            Mat[i,j] = float(Mat[i,j]-t[j])

    # covariance Matrix
    cov_Mat = np.dot(Mat.T, Mat)/(p-1)

    # PCA by original algorithm
    # eigvalues and eigenvectors of covariance Matrix with eigvalues descending
    U,V = np.linalg.eigh(cov_Mat) 
    # Rearrange the eigenvectors and eigenvalues
    U = U[::-1]
    for i in range(n):
        V[i,:] = V[i,:][::-1]
    # choose eigenvalue by component or rate, not both of them euqal to 0
    Index = index_lst(U, component=2)  # choose how many main factors
    if Index:
        v = V[:,:Index]  # subset of Unitary matrix
    else:  # improper rate choice may return Index=0
        print('Invalid rate choice.\nPlease adjust the rate.')
        print('Rate distribute follows:')
        print([sum(U[:i])/sum(U) for i in range(1, len(U)+1)])
        sys.exit(0)
    # data transformation
    T1 = np.dot(Mat, v)
    # print the transformed data
    print('We choose %d main factors.'%Index)
    print('After PCA transformation, data becomes:\n',T1)

    # PCA by original algorithm using SVD
    print('\nMethod 2: PCA by original algorithm using SVD:')
    # u: Unitary matrix,  eigenvectors in columns 
    # d: list of the singular values, sorted in descending order
    u,d,v = np.linalg.svd(cov_Mat)
    Index = index_lst(d, rate=0.95)  # choose how many main factors
    T2 = np.dot(Mat, u[:,:Index])  # transformed data
    print('We choose %d main factors.'%Index)
    print('After PCA transformation, data becomes:\n',T2)

    # PCA by Scikit-learn
    pca = PCA(n_components=2) # n_components can be integer or float in (0,1)
    pca.fit(mat)  # fit the model
    print('\nMethod 3: PCA by Scikit-learn:')
    print('After PCA transformation, data becomes:')
    print(pca.fit_transform(mat))  # transformed data

main()

参考资料：
1. 三种方法实现PCA算法(Python)
2. 主成分分析(PCA)原理详解
3. PCA为什么要用协方差矩阵
4. 机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用

利用Numpy的svd函数实现的PCA为什么是对协方差矩阵进行SVD分解

猜你喜欢