回顾：
前面讲了，飞行器坐标与地球坐标之间的夹角，就是我们要求的姿态。
姿态的表示方法有两类：无限转动法， 和有限转动法。
用于表示机体瞬间小角度变化的，是无限转动法。
其中常用于导航，工程计算的，表示最终姿态结果的，是有限转动法。
而我们可以通过特定转序，例如 ZXZ` 的“欧拉角”，来描述有限转动。
欧拉角的矩阵表示：
欧拉角的诞生，背后的故事，这里就不讲了。感兴趣可以搜索来看看。
总之，知道欧拉角是什么就行了：
当一个物体从姿势A ， 先绕自身的坐标X轴旋转a角，再Y绕轴转β角，最后绕Z轴旋转θ角，得到姿态B，那么它在XYZ序上的欧拉角就是{a,β,θ}；
（注意，欧拉角有12种旋转顺序，所以一定要清楚你用的是哪种顺序）
但是，如果我们用三角函数来表达欧拉角，会非常繁琐。好在数学家们很牛，他们发明了变换矩阵，用来描述欧拉角的变换。
1. 从容易理解的二维坐标入手：
首先，我们看看二维坐标的情况。假设有一个坐标XOY，为固定坐标。有一个坐标x`oy`，为转动坐标。他们最初是重合的。
当转动坐标系x`oy`（机体坐标）绕o点逆时针转动α角后，其状态如下：
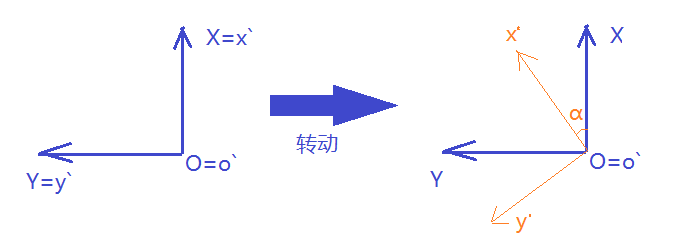
按照三角函数，机体坐标(x`oy`)在原坐标(XOY)中的关系表示如下：
那么，我们如果用矩阵来表述这个关系，就可以写为：
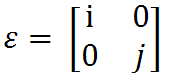（原坐标表达）
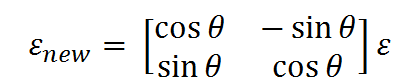(转动θ角后的坐标表达)
于是我们就有了坐标转换矩阵Cbn,它可以通过对原坐标E 做矩阵乘法，得到转动后的新坐标Enew。
注意，这个是坐标轴的转动，而如果是一个向量围绕O点做转动，那么变换矩阵就要取转置T了。
这里理解一下：
坐标轴逆时针转动，意味着原来坐标上的点，相对坐标轴顺时针转动。当坐标轴不动，向量转动逆时针转动时，相当于向量不变，坐标轴顺时针转动。
甚至，不仅仅是转动，它还可以表达拉升，扭曲等等转变。如果对自己数学有信心的小朋友们可以去尝试定量的理解（我就算了。。。）
那么，接下来就把二维的坐标系，扩展到三维空间。
2. 从二维扩大到三维：
如果用欧拉角来表示一次旋转，其实就是分解成了3次二维旋转（有限转动），所以，我们的变换矩阵也是由三个矩阵相乘得到。当然，虽然旋转是二维的，但矩阵元素一定是三维的。
先看看一个坐标转动的变换矩阵：
这描述了: Z轴固定的，绕Z旋转θ角的转动。可见，固定轴是 [0 0 1]
那么，当我们设定有限旋转的次序是 ZXY时，则一次完整的欧拉变换，需要用三个矩阵来标识:
当然，我们可以把三个矩阵乘起来，得到一个最终的变换矩阵
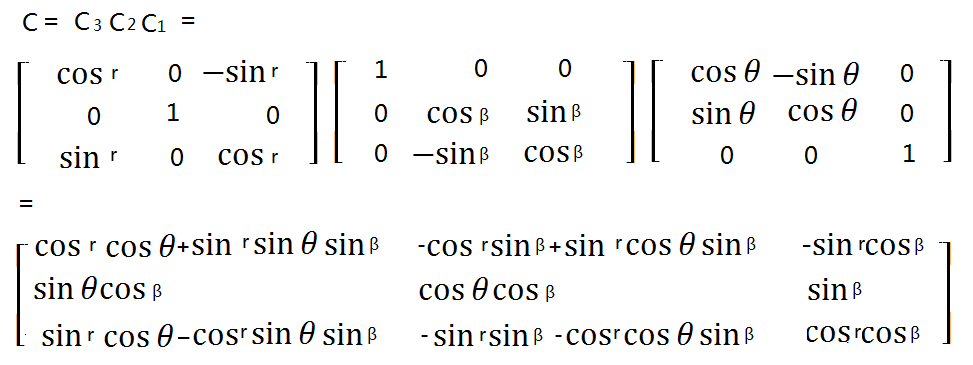
最终这个C矩阵，就是我们的有限旋转矩阵。可以直接用于计算了。
等等，还没完！
当r , θ, β 三个角足够小的时候，我们实际上可以忽略高阶小量，则可以得到矩阵C的另外一个表达
这个是无限旋转矩阵，它成立时有条件的，即三个转角都足够小。
它的意义是，我们如果使用这个矩阵来对陀螺仪的输出做累乘，实际上是可以得到一个初步的姿态的。
OK。 关于欧拉角的矩阵表示，就说到这里。
但是问题还没有结束，我们实际工作中，用的并不是欧拉角做计算，而是四元数。 那么接下来有空的时候，我再讲讲四元数的事情。