(2018浙江高考压轴题)
已知函数$f(x)=\sqrt{x}-\ln x.$
(2)若$a\le 3-4\ln 2,$证明:对于任意$k>0$,直线$y=kx+a$ 与曲线$y=f(x)$有唯一的公共点.

分析:等价于$k=\dfrac{\sqrt{x}-\ln x-a}{x}$有唯一解.记$g(x)=\dfrac{\sqrt{x}-\ln x-a}{x}$,则$g^{'}(x)=\dfrac{\ln x-\dfrac{\sqrt{x}}{2}-1+a}{x^2}$,
记$h(x)=\ln x-\frac{\sqrt{x}}{2}-1+a$,则$h^{'}(x)=\dfrac{4-\sqrt{x}}{4x}$,故$h(x)$在$(0,16)$单调递减$(16,+\infty)$单调递增.
所以$h(x)_{max}=h(16)=\ln(16)-3+a\le0$,所以$g^{'}(x)<0$,即$g(x)$单调递减.又$\lim\limits_{x\rightarrow0}(\dfrac{\sqrt{x}-\ln x-a}{x})= +\infty,\lim\limits_{x\rightarrow+\infty}(\dfrac{\sqrt{x}-\ln x-a}{x})=0$,故$k>0$时$y=k$与$g(x)=\dfrac{\sqrt{x}-\ln x-a}{x}$有且只有一个交点.
注:这里$a\le 3-4\ln 2$的条件可以考虑$f(x)=\sqrt{x}-\ln x.$的二阶导数的拐点$f^{''}(x)=-\dfrac{1}{4}x^{\frac{3}{2}}+x^{-2}=0$得拐点为$x=16$,求拐点处的切线方程:$y=\dfrac{1}{16}x+3-4\ln2$.
考虑$f(x)$的图像,当$a\le3-4\ln2$时,对于任意$k>0$,直线$y=kx+a$ 与曲线$y=f(x)$有唯一的公共点.
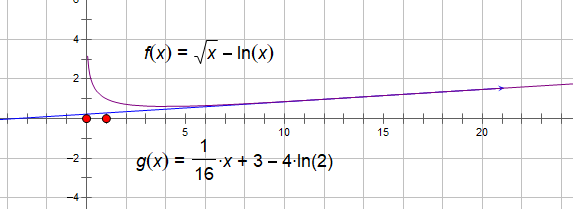
练习:若对任意$a>0$,函数$f(x)=x^3+ax^2+bx+1$在开区间$(-\infty,0)$内有且仅有一个零点,则实数$b$的取值范围_____
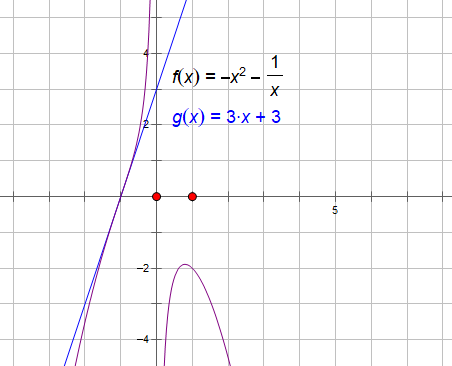
提示:只需考虑$y=ax+b$与$y=-x^2-\dfrac{1}{x}$图像交点,考虑拐点处切线方程:$y=3x+3$分析$y=-x^2-\dfrac{1}{x}$图像,易得$b\le3$
注:无非就是$b\ge3$或者$b\le3$,从图像中看若$b\ge3$,可以取$b$足够大,显然当$a>0$时可以有两个交点,故只有一个交点时$b\le3$