欧拉函数详解+例题：B - Farey Sequence

通过欧拉筛引入欧拉函数：

一般情况下,埃式筛就能解决大部分素数筛选的问题,但是也有可能有那种**出题人,非要出个1e7的变态数据去卡你,那么我们就介绍一种新的素数筛选方法,欧拉筛埃式筛的复杂度是O(nlglgn) 欧拉筛复杂度O(n) 一般的情况下,欧拉筛比埃式要快5-6倍

int prime[maxn],tot;
bool isprime[maxn];

void primeall(){

    memset(isprime,true,sizeof(isprime));
    
       for(int i=2;i<maxn;i++){
        
            if(idprime[i])    prime[tot++]=i;
    
       for(int j=0;j<tot&&i*prime[j]<maxn;j++){

            isprime[i*prime[j]]=false;

            if(i%prime[j]==0)       //和埃式筛的区别

                break;
            }
        }
    }

原理：

只用每个数最小的质因子去筛选它,所以每个数只会被筛选一次,复杂度O(n)

对于每个数i,枚举在此之前筛选出来的素数prime[j],

则 i*prime[j]一定不是素数

最关键的一步是保证每个数只会被它最小的质因子筛选

当在枚举prime[j]的时候，

if(i%prime[j]==0) 则说明prime[j]已经是i最小的质因子了终止循环。

为什么i%prime[j]==0 时终止循环就能保证每个数只筛选一次了？

if(i%prime[j]==0) 则i*prime[j+1]%prime[j]一定也等于0,

即为i*prime[j+1]的最小质因子为prime[j],

i*prime[j+1]只会被prime[j]筛选,

而不会被prime[j+1]这个较大的质因子筛选如此便保证了每个数只被筛选一次

欧拉函数定义：

在数论，对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目（φ(1)=1）。

此函数以其首名研究者欧拉命名(Euler's totient function)，它又称为Euler's totient function、φ函数、欧拉商数等。

对于正整数n，欧拉函数是小于等于n的正整数中与n互质的数的数目，表示为φ（n）

欧拉函数性质：

性质1：对于素数p，φ（p）=p-1

性质2：对于两个互质数p，q，φ（pq）=φ（p）*φ（q）=（p-1）（q-1）。（积性函数）

性质3：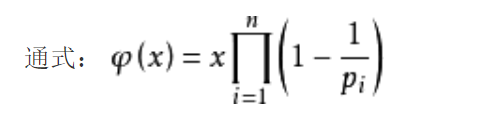

欧拉筛可以O(n)的复杂度筛选任何积性函数

如此,便可以用欧拉筛筛选欧拉函数

首先当i为素数的时候,oula[i]=i-1

其次进行筛选i*prime[j]的欧拉函数值

,当i与prime[j]互质,oula[i*prime[j]]=oula[i]*(prime[j]-1)

当prime[j]为i的最小质因子的时候,根据欧拉函数的通项公式,此时i与i*prime[j]的质因子种类相同,

则oula[i*prime[j]]=oula[i]*prime[j]。

伪代码：

int prime[maxn],tol,oula[maxn];

bool isprime[maxn];

void primeall(){

        memset(isprime,true,sizeof(isprime));

        for(int i=2;i<maxn;i++){

            if(isprime[i]){

                prime[tot++]=i;

                oula[i]=i-1;         //i为素数

        }

        for(int j=0; j<tot && prime[j]*i<maxn; j++){
            
            isprime[prime[j]*i]=false;
            
            if(i%prime[j]==0){
            
                oula[i*prime[j]]=oula[i]*prime[j];   //当prime[j]为i的最小质因子的时候

                break;

            }
             oula[i*prime[j]]=oula[i]*(prime[j]-1);       //当i与prime[j]互质
           }
        }

例题：B - Farey Sequence

The Farey Sequence Fn for any integer n with n >= 2 is the set of irreducible rational numbers a/b with 0 < a < b <= n and gcd(a,b) = 1 arranged in increasing order. The first few are
F2 = {1/2}
F3 = {1/3, 1/2, 2/3}
F4 = {1/4, 1/3, 1/2, 2/3, 3/4}
F5 = {1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5}

You task is to calculate the number of terms in the Farey sequence Fn.

Input

There are several test cases. Each test case has only one line, which contains a positive integer n (2 <= n <= 10 6). There are no blank lines between cases. A line with a single 0 terminates the input.

Output

For each test case, you should output one line, which contains N(n) ---- the number of terms in the Farey sequence Fn.

Sample Input

Sample Output

已AC题解

#include<stdio.h>
#include<algorithm>
#include<cstring>
#define ll long long
using namespace std;
const int INF=1e6+7;
bool vis[INF];
ll prime[INF];
ll cot=0;
ll oula[INF];
void make_prime()
{
	memset(vis,true,sizeof(vis));
	for(ll i=2;i<INF;i++)
	{
		if(vis[i])
			{
				prime[cot++]=i;
				oula[i]=i-1;
			}
		for(ll j=0;j<cot&&i*prime[j]<INF;j++)
		{
				vis[i*prime[j]]=false;
			if(i%prime[j]==0)
			{
				oula[i*prime[j]]=oula[i]*prime[j];
					break;
			}
				oula[i*prime[j]]=oula[i]*(prime[j]-1);
		}
	}
}
int main()
{
	make_prime();
	int n;
	while(~scanf("%d",&n)&&n)
	{
		ll ans=0;
			for(ll i=2;i<=n;i++)
				ans+=oula[i];
		printf("%lld\n",ans);
	}
}

欧拉函数详解+例题：B - Farey Sequence

猜你喜欢