【树状数组】区间修改区间查询

树状数组

树状数组是一种~~简单的~~ 维护前缀和的数据结构，可以直接实现单点修改和区间查值。将数组进行差分后，树状数组还可以进行区间修改区间查询。

区间修改
利用差分数组即可实现，利用差分数组即可实现，将区间[l,r]加上v即将差分数组的d[l]加上v并将的d[r+1]减去v。

区间查询
首先对于差分数组d,序列a，前缀和S，满足以下性质：
$\ a[x]=\sum_{i=1}^{i<=x}d[i]$
$\ S[x]=\sum_{i=1}^{i<=x}a[i]$
由此我们可以得到：
$\ S[x]=\sum_{i=1}^{i<=x}\sum_{j=1}^{j<=i}d[j]$
化简可以得到：
$\ S[x]=\sum_{i=1}^{i<=x}d[i]*(x-i+1)$
$\ S[x]=\sum_{i=1}^{i<=x}d[i]*(x+1)-\sum_{i=1}^{i<=x}d[i]*i$
如果我们使用两个树状数组，分别维护d[i]和d[i]*i，那么就可以~~轻松地~~ 进行区间查询了，单次查询时间复杂度O(log^2 n)。
代码：

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<queue>
#include<algorithm>
#define re register
using namespace std;
int a,b,n,m,t,now=0;
long long val;
const int mod=32001;
inline int low(int x){return x&(-x);}
struct node{//树状数组封装 
 long long c[100001];
 inline void begin(int _n)
 {
  n=_n;
  memset(c,0,sizeof(c));
 }
 inline void change(int k,long long v)
 {
  while(k<=n)
  {
   c[k]+=v;
   k+=low(k);
  }
 }
 inline long long ask(int k)
 {
  long long ret=0;
  while(k>0)
  {
   ret+=c[k];
   k-=low(k);
  }
  return ret;
 }
}A,B;
int main()
{
 scanf("%d%d",&n,&m);
 A.begin(n);
 B.begin(n);
 for(int re i=1;i<=n;i++)
 {
  scanf("%d",&a);
  A.change(i,a-now);
  B.change(i,(a-now)*i);
  now=a;
 }
 for(int re i=1;i<=m;i++)
 {
  scanf("%d",&t);
  if(t==1)
  {
   scanf("%d%d%lld",&a,&b,&val);//修改区间 
   A.change(a,val);A.change(b+1,-val);
   B.change(a,a*val);B.change(b+1,-(b+1)*val);
  }
  else
  {
   scanf("%d%d",&a,&b);//查询区间 
   a--;
   long long l=(a+1)*A.ask(a)-B.ask(a);
   long long r=(b+1)*A.ask(b)-B.ask(b);
   printf("%lld\n",r-l);
  }
 }
}

以上结论可以推广到二维：
$\ S[x][y]=\sum_{i=1}^{i<=x}\sum_{j=1}^{j<=y}d[i][j]*(x-i+1)*(y-j+1)$
拆开可以得到:
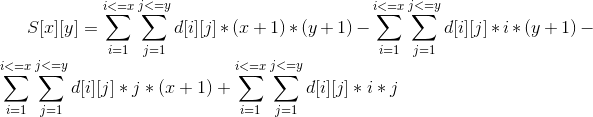
在这里插入图片描述
结合二维前缀和和二维的差分数组,于是我们可以维护四个值来解决d[i][j],d[i][j]*i,d[i][j]*j,d[i][j]*i *j。
~~看起来似乎很简单！~~

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<queue>
#include<algorithm>
#define re register
using namespace std;
int a,b,n,m,t,now=0;
long long val;
const long long mod=32001;
inline long long low(long long x){return x&(-x);}
struct node{
 long long c[1<<11|1][1<<11|1];
 inline void change(long long x,long long y,long long v)
 {
  long long temp=y;
  while(x<=n)
  {
   y=temp;
   while(y<=m)
   {
    c[x][y]+=v;
    y+=low(y);
   }
   x+=low(x);
  }
 
 }
 inline long long ask(long long x,long long y)
 {
  long long ret=0,temp=y;
  while(x>0)
  {
   y=temp;
   while(y>0)
   {
    ret+=c[x][y];
    y-=low(y);
   }
   x-=low(x);  
  }
  return ret;
 }
}A,B,C,D;//A:dij B:i C:j D:i*j
long long a1,a2,a3,a4;
long long b1,b2,b3,b4;
long long n1,n2,n3,n4;
inline long long get(int a,int b)
{
 a1=A.ask(a,b)*(a+1)*(b+1);
 a2=B.ask(a,b)*(b+1);
 a3=C.ask(a,b)*(a+1);
 a4=D.ask(a,b);
 return a1+a4-a2-a3;
}
int main()
{
 scanf("%d%d",&n,&m);
 while(scanf("%d",&t)!=EOF)
 {
  long long a,b,c,d;
  if(t==1)
  {
   scanf("%d%d%d%d%lld",&a,&b,&c,&d,&val);
   A.change(a,b,val);B.change(a,b,a*val);C.change(a,b,val*b);D.change(a,b,val*a*b);
   A.change(c+1,d+1,val);B.change(c+1,d+1,(c+1)*val);C.change(c+1,d+1,val*(d+1));D.change(c+1,d+1,val*(c+1)*(d+1));
   A.change(a,d+1,-val);B.change(a,d+1,-val*a);C.change(a,d+1,-val*(d+1));D.change(a,d+1,-val*a*(d+1));
   A.change(c+1,b,-val);B.change(c+1,b,-val*(c+1));C.change(c+1,b,-val*b);D.change(c+1,b,-val*(c+1)*b);
  }
  else
  {
   scanf("%d%d%d%d",&a,&b,&c,&d);
   a--,b--;
   printf("%lld\n",get(c,d)+get(a,b)-get(c,b)-get(a,d));
  }
 }
}

补充：二维差分数组的推导
利用二维前缀和，我们可以进行如下推导。
设二维数组a的差分数组为d，由差分数组定义可得：
$\ a[x][y]=\sum_{i=1}^{i<=x}\sum_{j=1}^{j<=y}d[i][j]$
$\ a[x][y]=d[x][y]-\sum_{i=1}^{i<=x}\sum_{j=1}^{j<=y-1}d[i][j]-\sum_{i=1}^{i<=x-1}\sum_{j=1}^{j<=y}d[i][j]+\sum_{i=1}^{i<=x-1}\sum_{j=1}^{j<=y-1}d[i][j]$
$\ a[x][y]=d[x][y]-a[x][y-1]-a[x-1][y]+a[x-1][y-1]$
$\ d[x][y]=a[x][y]+a[x][y-1]+a[x-1][y]-a[x-1][y-1]$
其实就是二维前缀和的逆运用。
~~上面的证明不是显而易见吗？~~

【树状数组】区间修改区间查询

树状数组

猜你喜欢