KMP算法,又称模式匹配算法,能够在线性时间内判定字符串 A[1~N] 是否为字符创 B[1~M] 的子串,并求出字符串 A 在字符串 B 中各次出现的位置。——《算法竞赛进阶指南》
食用须知:
*本文的字符串下标以 0 开始。字符串范围:字符串 A[0~N-1],字符串 B[0~M-1]。
*以下概念来自个人理解,并不十分准确。慎!
<KMP思想与模板>
首先,O(NM)的朴素做法是:尝试枚举字符串 B 的每一个位置 i 。每确定一个位置 i ,枚举判断 A[0] 与 B[i] 、A[1] 与 B[i+1] ...... A[N-1] 与 B[i+N-1]是否一一相等(即称为"匹配"),如果相等,答案累加,i 指针往后移动;如果不相等,则 i 指针直接往后移动一位,直到不能再往后移动(i+N-1>=M-1)时,停止。
KMP算法能够更高效、更准确地处理这个问题,并且,我们可以通过KMP算法获得其他一些信息。
这里,给出几个 概念:
- 前缀:字符串 A 的前缀即为字符串 A 中区间 0~0、0~1 ...... 0~N-1 所构成的子串。
- 后缀:与前缀相仿,字符串 A 的后缀即为字符串 A 中区间 N-1~N-1、N-2~N-1 ...... 0~N-1 所构成的子串。
举个栗子:
| A | "abcab" |
| 前缀 |
"a","ab","abc","abca","abcab" |
| 后缀 | "b","ab","cab","bcab","abcab" |
- next 数组:next[i] 表示 " A 中以 i 结尾的非前缀 " 与 " A 的前缀 " 能够匹配的最长长度。(以 i 结尾的非前缀:即字符串1~i的后缀。在以上的例子中,当 A="abcab",i=N-1 时,以 i 结尾的非前缀即为:"b","ab","cab","bcab")
举个栗子:
| A | "abcab" |
| i = 0 | next[0]=0 |
| i = 1 | next[1]=0 |
| i = 2 |
next[2]=0 |
| i = 3 | next[3]=1( "a"与"a" ) |
| i = 4 | next[4]=2("ab"与“ab") |
KMP算法分为 两步 :
- 对于字符串 A 进行自我"匹配":求出一个数组 next 。
- 将字符串 A 与 B 进行与第一步类似的"匹配"操作。
字符串 A 的自我"匹配"(即 next 数组的实现过程):
我们将字符串 A 复制成两个相同的字符串 A 和 A' (*分成两个相同的字符串仅为了方便比较)。i 指针指向在字符串 A 中所匹配到的位置,j 指向在字符串 A' 中所匹配到的位置(即时,所要求的是next[i])。如图:

当 A[i]==A'[j] (相当于能够继续"匹配"),next[i]=++j 。
当 A[i]!=A'[j] ,j=next[j-1](查找前面连续的能够尽量匹配的数),直到 A[i]==A[j] 或 j==0 时停止。
再给出一个例子:
开始时,next[0]=0
当 i = 1,j =0 时(*因为是" 非前缀 " 与 " 前缀 " 的匹配,所以 "a" 不能与 "a" 匹配),j=next[0]=0,由此,next[1]=0
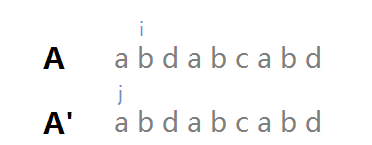
当 i = 2,j = 0 时,A[i]!=A'[j] , j=next[1]=0,由此,next[2]=0

当 i = 3 ,j = 0 时,A[i]==A'[j] , next[3]=++j=1

当 i = 4,j = 1 时,A[i]==A'[j],next[4]=++j=2

当 i = 5,j = 2 时 ,A[i]!=A[j],j=next[4]=2,这时,依旧 A[i]!=A[j],j=next[1]=0

......如此类推,代码实现如下(A 与 A' 不再分开计算):
int j=0; nxt[0]=0;
for(int i=1;i<A.size();i++){
for(;A[i]!=A[j]&&j;) j=nxt[j-1];
if(A[i]==A[j]) j++;
nxt[i]=j;
}字符串 A 与 字符串 B 匹配:
思路类似,不再详述。代码实现如下:
j=0;
for(int i=0;i<B.size();i++){
for(;B[i]!=A[j]&&j;) j=nxt[j-1];
if(B[i]==A[j]) j++;
if(j>=A.size()) ans++;//ans统计B中含多少个A子串
}线性复杂度玄学证明(by hzk)
对于外层循环,复杂度为O(N)。
对于内层循环,只有 j > 0 时才进行,而 j 又只加 N 次 。
∴ 很线性
如果没听懂,就多抄代码。——by hzk
<KMP周期(最小循环长度)>
这样的题目很多,例如
给你一个字符串,它是由某个字符串不断自我连接形成的。
但是这个字符串是不确定的,现在只想知道它的最短长度是多少。
样例输入: cabcabca
样例输出:3
样例解释:可由 "cab" 不断自我连接得到 "cabcabcab","cabcabca" 是它的子串。
给出的读入是由循环节不断自我连接得到的字符串的子串,与直接的求最短循环节相等。思路:KMP模板,答案为 N-A[N-1](1 开始则为:N-A[N])。
论证:如果存在循环节,字符串 0~i 的最短循环长度为 i-next[i]。
伪证:
当next[i]=0时,0~i 整个字符串为循环节,结论显然(by hzk)成立.
当next[i]>0时,必然会出现这样的情况:

(图片出处:https://blog.csdn.net/hzk_cpp/article/details/87895335 %% by hzk)
黑色的表示字符串A,红色为最大匹配(也就是说两条线段长度为 next[i])。最末行的两条蓝色线段相等,由匹配的结果可得,每上下覆盖的两条线段都相等,那么显然(by hzk)在蓝色的线段都必须相等。
当next[i]%(i-next[i])!=0,即表示红色线段不能被不重叠的蓝色线段完全覆盖,那么就不能构成完整的循环节。否则,循环节就为(i-next[i])。以上给出的例题则不需要判断,因为不需要构成完整的循环节。
对于例题,代码如下:
cin>>s;
int N=s.size();
int j=0;
for(int i=1;i<N;i++){
for(;s[i]!=s[j]&&j;) j=nxt[j-1];
if(s[i]==s[j]) j++;
nxt[i]=j;
}
printf("%d",N-nxt[N-1]);
return 0;