统计学笔记（一）：数据概括性度量

一、集中趋势的度量

集中趋势是指一组数据向某一中心值靠拢的程度，它反映了一组数据中心点的位置所在。主要的度量有：众数、中位数、平均数、加权平均数、几何平均数等。

众数

一组数据中出现次数最多的变量值。

中位数

一组数据排序后处于中间位置上的变量值。

平均数

$\bar{x}=\frac{\sum_{i=1}^{n}x_{i}}{n}$

加权平均数

分为k组，各组的中值分别用 $M_{1}...M_{k}$ 表示，各组变量值出现的频数分别用 $f_{1}...f_{k}$ 表示，则样本加权平均数为：

$\bar{x}=\frac{M_{1}f_{1}+M_{2}f_{2}+...+M_{k}f_{k}}{f_{1}+f_{2}+...+f_{k}}=\frac{\sum_{i=1}^{k}M_{i}f_{i}}{n}$

几何平均数

n个变量乘积的n次方根，用 $G$ 表示：

$G=\sqrt[n]{x_{1}x_{2}...x_{n}}=\sqrt[n]{\prod_{i=1}^{n}x_{i}}$

主要用于计算平均比率。当所掌握的变量值本身是比率的形式时，采用几何平均数计算平均比率更合理，在实际应用中，几何平均数主要用于计算现象的平均增长率。

二、离散趋势的度量

离散程度与集中趋势相反，其反映的是各变量值远离其中心值的程度。数据的离散程度越大，集中趋势的测度值对该组数据的代表性就越差；离散程度越小，其代表性就越好。

描述数据离散程度采用的测量值，根据数据类型的不同主要有异众比率、四分位差、方差和标准差。此外，还有极差、平均差以及测度相对离散程度的离散系数等。

异众比率

异众比率表示非众数组的频数占总频数的比例，用 $V_{r}$ 表示：

$V_{r}=\frac{\sum f_{i}-\sum f_{m}}{\sum f_{i}}=1-\frac{\sum f_{m}}{\sum f_{i}}$

主要用于测量众数对一组数据的代表程度， $V_{r}$ 越大，则众数代表性越差，适合用于测度分类数据的离散程度。

四分位差

上四分位数与下四分位数之差，用 $Q_{d}$ 表示：

$Q_{d}=Q_{U}-Q_{L}$

反映了中间50%数据的离散程度，其数值越小，说明中间的数据越密集。主要用于测度顺序数据的离散程度，不适用分类数据。

平均差

各变量值与平均数离差绝对值的平均数， $M_{d}$ 用表示。

未分组数据的平均差：

$M_{d}=\frac{\sum_{i=1}^{n}\left | x_{i}-\bar{x} \right |}{n}$

分组数据的平均差：

$M_{d}=\frac{\sum_{i=1}^{n}\left | M_{i}-\bar{x} \right |f_{i}}{n}$ （ $M_{i}$ 为各组的中值， $f_{i}$ 为各组的频数）

平均差以平均数为中心，反映了每个数据与平均数的平均差异程度。它能全面准确地反映一组数据地离散状况。平均差越大，说明数据的离散程度越大；反之则说明数据的离散程度小（平均差实际应用比较少）

方差

各变量值与平均数离差平方的平均数。通过平方的办法消去离差的正负号，然后再进行平均。方差(或标准表)能较好反映出数据的离散程度（实际应用比较广泛）

未分组数据的方差：

$s^{2}=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}{n-1}$

分组数据的方差：

$s^{2}=\frac{\sum_{i=1}^{k}(M_{i}-\bar{x})^{2}f_{i}}{n-1}$

（自由度为n-1，即只有n-1个值可以自由取值，剩下一个的值由n-1个自由值确定而确定）

相对位置的度量

(i) 标准分数

变量值与其平均数的离差除以标准差后的值，也称为z分数：

$z_{i}=\frac{x_{i}-\bar{x}}{s}$

标准分数给出了一组数据中各数值的相对位置。比如某个数值的标准分为为-1.5，就知道该数值低于平均数1.5倍的标准差。

标准分数具有平均数为0，标准差为1的特性。比如一组数据为25，28，31，34，37，40，43，其平均数为34，标准差为6，其标准分数变换图如下：

(ii) 经验法则

在 $\pm 3$ 个标准差之外的数据，在统计上称为离群点。

(iii) 切比雪夫不等式

经验法则适合对称的数据，切比雪夫对任何分布形状的数据都适用。

根据切比雪夫不等式，至少由 $(1-\frac{1}{k^{2}})$ 的数据落在 $\pm k$ 个标准差之内。

相对离散程度：离散系数

为消除变量值水平高低和计量单位不同对离散程度测量值的影响，需要计算离散系数：

$V_{s}=\frac{s}{\bar{x}}$ （ $s$ 为标准差）

离散系数是测度数据离散程度的相对统计量，主要是用于比较不同样本数据的离散程度。离散系数大，说明数据的离散程度也大。

总结：对于分类数据，主要用异众比率来测度其离散程度；

对于顺序数据，主要用四分位差来测度其离散程度；

对于数值型数据，主要是用方差或标准差来测度其离散程度；

当需要对不同样本数据的离散程度进行比较时，则使用离散系数。

三、偏态与峰态的度量

偏态及其度量

偏态（skewness）是对数据分布对称性的测度，统计量为偏态系数 $SK$ ：

$SK=\frac{n\sum (x_{i}-\bar{x})^{3}}{(n-1)(n-2)s^{3}}$

数据的分布是对称的，则偏态系数 $SK$ 等于0。

分组数据的偏态：

$SK=\frac{\sum_{i=1}^{k}(M_{i}-\bar{x})^{3}f_{i}}{ns^{3}}$

当分布对称时，离差三次方后正负离差可以相互抵消，因而SK的分子等于0，则SK=0；当分布不对称时，正负离差不能抵消，就形成了正或负的偏态系数SK。当SK为正值时，表示正离差值较大，可以判断为正偏或右偏；反之，当SK为负值时，表示负离差值较大，可判断为负偏或左偏。

峰态及其度量

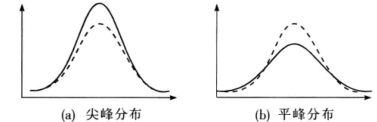
峰态（kurtosis）是对数据分布平峰或尖峰程度的测度，其统计量为峰态系数 $K$ ：

$K=\frac{n(n+1)\sum (x_{i}-\bar{x})^{4}-3\left [ \sum (x_{i}-\bar{x})^{2} \right ]^{2}(n-1)}{(n-1)(n-2)(n-3)s^{4}}$

峰态通常是与标准正态分布相比较而言的。如果一组数据服从标准正态分布，则峰态系数的值等于0；若峰态系数的值明显不等于0，则表明分布比正态分布更平或更尖，通常称为平峰分布或尖峰分布，如下图：

分组数据的峰态系数：

$K=\frac{\sum_{i=1}^{k}(M_{i}-\bar{x})^{4}f_{i}}{ns^{4}}$

通过与标准正态分布的峰态系数进行比较，来说明分布的尖峰和扁平程度。由于正态分布的峰态系数为0，当K>0时为尖峰分布，数据的分布更集中；当K<0时为扁平分布，数据的分布越分散。

统计学笔记（一）：数据概括性度量

一、集中趋势的度量

二、离散趋势的度量

三、偏态与峰态的度量

猜你喜欢