POINT 1 二分
二分的思想
给定一个单调的函数/数组
给定一个值,求这个值是否存在
或者找到这个值应当存在的位置
由于数组有序,不妨认为他单调递增
假设Ai > x,则必然有∀j > i, Aj > x
假设Aj < x,则必然有∀j < i, Aj < x
二分的原理就是每次在待定区间中选择mid。
必然可以确定一边是没有意义的。每次问题的规模缩小 1/2
因此复杂度为O(logN)
寻找<=x的第一个位置
如果两次二分找到的中点一样的话,就说明已经二分完了
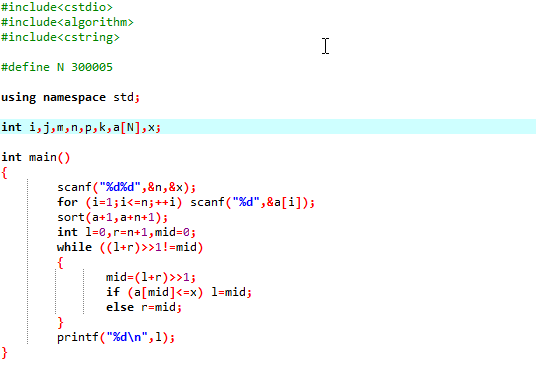
最后是答案是存在变量L中
注意一定要是单调序列
二分答案
顾名思义,就是对答案进行二分
对于某些要求“满足某条件的最小值”类的问题,对答案进
行二分,假设答案不超过mid,则问题变为“满足某条件且
某值不超过mid”的判定性问题。
常用于最大值最小化类问题。
在二分答案之后往往需要一个贪心策略。
例一
一条河上有n个石子排成一条直线,第i个石子距离河岸xi。
一只年长的青蛙想要从岸边(x=0处)到达第n个石子上(其实
是对岸)。这只青蛙实在是太年长了,所以最多只能
跳m次,而且他希望他这些次跳跃中距离最远的那次距离尽
可能的短。请你帮他求出这个最远距离最短能是多少。
1 ≤ m ≤ n ≤ 105
最小化:最大的跳跃距离
二分答案:设答案为mid,则问题变为:
n个石子,只能跳m次,每次跳远距离不能超过mid,问是否
可行。
或者n个石子,每次最远距离不超过mid,问最少跳多少次
(然后和m比较即可)。
贪心策略:每次跳的尽量远即可
二分O(logN)*贪心O(N)=O(NlogN)
先检查是否能跳的过去
再让他在不超过最远距离的情况下多跳
如果他跳的步数不大于m就可行
例二
给定n个物品,每个物品有属性Ai和Bi。
要求在其中选择k个物品,使得选择的物品
的sum(A)/sum(B)尽可能大。
贪心:选Ai/Bi最高的k个物品?
反例:
3 2
1000 10
1000 100
1 1
除了最优的物品一定会选之外 可以考虑选择Bi非常小的物
品, 减小对性价比的影响。此时物品3比物品2 更优。
二分答案
假设sum(Ai)/sum(Bi) >= mid
则:sum(Ai) - mid * sum(Bi) >= 0
即:sum(Ai-mid*Bi) >= 0
将Ai-mid*Bi作为第i个物品的权值,问题变为能否选k个物品
使得权值和大于0.此时贪心选择权值最大的k个物品即可。
二分O(logN)* 排序O(NlogN) = O(Nlog 2N)
二分是对一个单调的函数进行的操作
那么我们有没有办法对一个单峰的函数进行操作呢?
求一个单峰函数的极值点
三分函数
三分



发现共性:l,r中值较小的那一段一定会被舍去
严格的实现每次都能缩小问题的 13
事实上我们取两次mid会好写很多,只是常数问题
例一
初始有一个为空的集合,要求支持两种操作
1.不断向集合中插入一个数,且这个数比集合中所有数都大
2.在集合中找一个子集,使得找到的子集S中的最大值减去
子集S中元素的平均值的差最大,并输出这个差
操作数≤ 500000
最大值肯定要选,可以自己证明一下
然后使其他数尽可能小
如何选取子集?
最后插入的这个数是一定要选的,然后再选小的数
就是一个最大数加上几个用来拉低平均值的小数构成了所需
子集
小数一定是从最小值开始连续增加使平均值减小,直到达到
一个临界点
再增加小数就会使平均值增大,易知这是一个单峰函数
因此考虑三分选多少小数即可
让上线稍微大一些
check:取前k个的和

(前x-1小的数+a[n])/x
main:

其他的三分就是更改check函数
分治的思想
将一个问题划分成若干个(一般都是分成俩)子问题
分别解决每个子问题后(也可能是前,还可能一前一后之类
的)
将各个子问题组合起来得到原问题的答案。
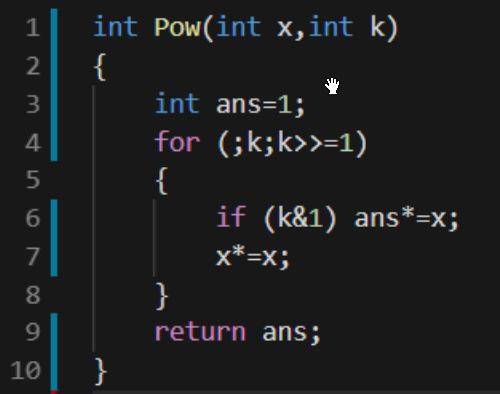
快速幂
如何快速计算X k?
我们将k进行二进制拆分。
比如我们需要计算X 11即我们需要计算X 20+21+23
因此我们只需要计算logk 次即可
归并排序
基本思想:先将整个数组分成两个部分,分别将两个部分排
好序,然后将两个排好序的数组O(n)合并成一个数组。
我们将问题分为两个阶段:分、治
分
对于每个长度> 1的区间,拆成两个[l, mid]区间
和[mid + 1, r]区间
直接递归下去
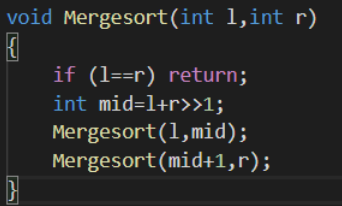
治
我们认为在处理区间[l,r]时,已经有[l,mid]和[mid+1,r]内分
别有序
这一次的操作就是合并两个有序序列,成为一个新的长有序
序列
用两个指针分别指向左右分别走到哪了即可
比较两个指针的值
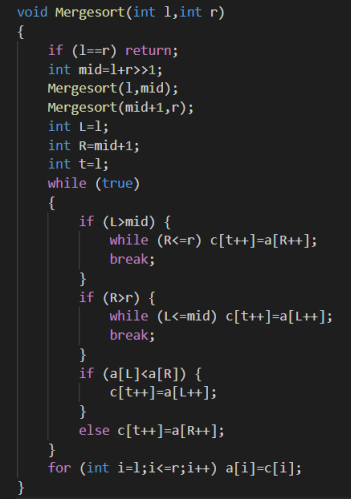
复杂度O(nlogn)是一个严格的算法
逆序对
给定一个1 ∼ n的排列,求逆序对数量。
1 ≤ n ≤ 105
逆序对:对于1 ≤ x < y ≤ n, 若A[x] > A[y],则称(x,y)为一
个逆序对。
题解
首先显然我们枚举x,y可以做到O(N2)
分治:
假设当前问题 Work(l,r) 是求l到r区间内的逆序对数量。
讨论所有(x,y)可能在的位置:
l ≤ x < y ≤ mid :子问题Work(l,mid)
x ≤ mid < y : ???
mid + 1 ≤ x < y ≤ r :子问题Work(mid+1,r)
对于每个mid右边的数,我们要找到mid左边有多少比它大
的数。
1) 对左侧排序,右侧在左侧上二分即可。 总时间复杂
度O(nlog2n)
2) 归并排序:
对于数组A和数组B的归并过程,每当我们将B中的元素取出
时:说明A中最小的元素比该元素大:说明A中所有元素比
该元素大:说明 答案+=A.size()
归并过程时间复杂度O(n),总时间复杂度O(nlogn)。
例二
有一个序列,初始时只有一个数n
对于序列中每一个> 1的数,拆分成三个数n/2,n%2,n/2并替
换原数。
直到序列中没有> 1的数为止
查询最终序列中[l, r]中有多少1
0 ≤ n < 250, 0 ≤ r - l ≤ 105

平面最近点对
给定二维平面上的N个点,求任意两点间的最近距离(欧几
里得距离)。
1 ≤ n ≤ 105
题解
不妨按照x坐标排序。对于区间[l,r],我们将其分成mid左右
两个部分。
两个点都在左侧:子问题Work(l,mid)
两个点都在右侧:子问题Work(mid+1,r)
两个点一个在左侧,一个在右侧 :
不妨按照x坐标排序。对于区间[l,r],我们将其分成mid左右
两个部分。
两个点都在左侧:子问题Work(l,mid)
两个点都在右侧:子问题Work(mid+1,r)
两个点一个在左侧,一个在右侧:
重点考虑第三种情况
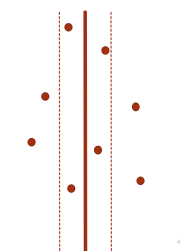
不妨假设左右两个子问题的答案为ans。则我们只需要考虑
分界线两边距离不超过ans以内的点即可。

不妨假设左右两个子问题的答案为ans。则我们只需要考虑
分界线两边距离不超过ans以内的点即可。
不妨假设左右两个子问题的答案为ans。则我们只需要考虑
分界线两边距离不超过ans以内的点即可。

对于每个点,可能和它距离不超过ans的点坐标范围
横坐标:[mid-ans,mid+ans]
纵坐标:[y-ans,y+ans]
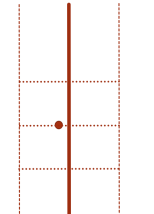
每个小正方形内点数不可能超过一个(因为任意两点距离不
低于ans)。故总点数不超过6个。除去该点自身,该点至多
需要和其他6个点求距离。
故该部分复杂度不超过O(n)。实现时可以直接对所有点按
照y坐标排序,O(n log2 n),或者使用归并排序的技巧,直
接O(n log n)即可。
