排队论模型（五）：有限源排队模型、服务率或到达率依赖状态的排队模型

1. 有限源排队模型

现在，来分析一下顾客源为有限的排队问题。这类排队问题的主要特征是顾客总数是有限的，如果有 m 个顾客。每个顾客来到系统中接受服务后仍回到原来的总体，还有可能再来，这类排队问题的典型例子是机器看管问题。如一个工人同时看管 m 台机器，当机器发生故障时即停下来等待维修，修好后再投入使用，且仍然可能再发生故障。类似的例子还有m 个终端共用一台打印机等，如图 2 所示。

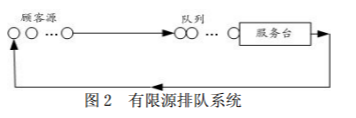
关于顾客的平均到达率，在无限源的情形中是按全体顾客来考虑的，而在有限源的情形下，必须按每一顾客来考虑。设每个顾客的到达率都是相同的，均为λ（这里λ 的含义是指单位时间内该顾客来到系统请求服务的次数），且每一顾客在系统外的时间均服从参数为 λ 的负指数分布。由于在系统外的顾客的平均数为 m − Ls ，故系统的有效到达率为

下面给出系统的有关运行指标

例 7 设有一工人看管 5 台机器，每台机器正常运转的时间服从负指数分布，平均为 15 分钟。当发生故障后，每次修理时间服从负指数分布，平均为 12 分钟，试求该系统的有关运行指标。

解用有限源排队模型处理本问题。已知

即该工人每小时可修理机器的平均台数为0.083× 60 = 4.96台。上述结果表面，机器停工时间过长，看管工人几乎没有空闲时间，应采取措施提高服务率或增加工人。 LINGO 计算程序如下

model:
lamda=1/15;mu=1/12;rho=lamda/mu;s=1;m=5;
load=m*rho;
L_s=@pfs(load,s,m);
p_0=1-(m-L_s)*rho;
lamda_e=lamda*(m-L_s);
p_5=@exp(@lgm(6))*0.8^5*p_0;
L_q=L_s-(1-p_0);
w_s=L_s/lamda_e;w_q=L_q/lamda_e;
end

2 服务率或到达率依赖状态的排队模型

在前面的各类排队模型的分析中，均假设顾客的到达率为常数 λ ，服务台的服务率也为常数 μ 。而在实际的排队问题中，到达率或服务率可能是随系统的状态而变化的。例如，当系统中顾客数已经比较多时，后来的顾客可能不愿意再进入系统；服务员的服务率当顾客较多时也可能会提高。因此，对单服务台系统，实际的到达率和服务率（它们均依赖于系统所处的状态n ）可假设为