数字图像处理第三章

数字图像处理---频域处理

（一）二维离散傅里叶变换
（二）在 MATLAB 中计算及观察二维 DFT
（三）频域滤波

3.1基础知识
3.2 DFT 滤波的基本步骤
3.3 频域滤波的M-函数

数字图像处理—频域处理

（一）二维离散傅里叶变换

基本定义：

二维离散傅里叶变换：(Two-Dimensional Discrete Fourier Transform)是一种数字变换方法，一般应用于将图像从空间域转至频域，在图像增强、图像去噪、图像边缘检测、图像特征提取、图像压缩等等应用中都起着极其重要的作用。
频谱：对一个时域信号进行傅里叶变换，就可以得到的信号的频谱，信号的频谱由两部分构成：幅度谱和相位谱，相位谱描述各个分量的相位随角频率的变化。幅度谱描述各个分量的幅度随着频率的变化。
功率谱：为信号频谱的平方。可观察图像的能量分布，如果频谱图中暗的点数更多，那么实际图像是比较柔和的（因为各点与邻域差异都不大，梯度相对较小），反之，如果频谱图中亮的点数多，那么实际图像一定是尖锐的，边界分明且边界两边像素差异较大的。
相位：表示相对于原始波形，这个波形的偏移量（左或右）。
频域：频域就是频率域，平常我们用的是时域，是和时间有关的，这里只和频率有关，是时间域的倒数。时域中，X轴是时间，频域中是频率。频域分析就是分析它的频率特性。

进一步直观的理解这几个定义，编写代码如下：

h = imread('D:\数字图像处理\第三章学习\cat2.jpg');
f = im2double(rgb2gray(h));    %把图像变为灰度图像
F = fft2(f);                   %对图像进行傅里叶变换
FF = fftshift(F);              %对图像频谱进行移动，使0频率点在中心
s=log(abs(FF));                %获得傅里叶变换的幅度谱
p=log(angle(FF)*180/pi);       %获得傅里叶变换的相位谱
figure;
subplot(1, 3, 1), imshow(h), title('原图像');
subplot(1, 3, 2), imshow(s), title('图像的傅里叶变换幅度谱');
subplot(1, 3, 3), imshow(p), title('图像的傅里叶变换相位谱');

代码运行效果如下：

傅立叶频谱图上我们看到的明暗不一的亮点，实际是图像上某一点与邻域点差异的强弱，即梯度的大小，也即该点的频率的大小，图像中的低频部分（能量大，呈现白色）指低梯度的点，高频部分（能量小，呈现黑灰色）反之。

理论推导：

令f(x,y)代表一幅大小为 MxN的数字图像，其中x=0,1,2,…,M-1, y=0,1,2,…,N-1, 由 F(u,v)表示的f(x,y)的二维离散傅立变换(DFT)可以由下式给出:
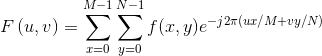
在这里插入图片描述
其中u=0,1,2,…,M-1,v=0,1,2,…,N-1。我们可以借助决定频率的变量 u、v(x和 y求和) 将指数形式展开为正弦和余弦的形式。频域系统是以 u,v(频率)为变量来表示 F(u, v)的坐标系。离散傅立叶反变换(IDFT)的形式为：

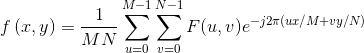
其中x=0,1,2,…,M-1,y=0,1,2,…,N-1。。因此，给定 F(u， v), 我们可以借助 IDFT(傅立叶反变换)来得到f(x,y)。

注意：由于 MATLAB中的 数组索引以1 开头，而不是以0 开头，MATLAB中的F(1,1)和f(1,1)对应数学公式中正变换和反变换的F(0,0)和f(0,0)。一般而言，F(i,j)= F(i-1,j-1),且f(i,j)= f(i-1,j-1) i=1 2,…,M且j=1,2,…,N。

傅立叶谱可以定义如下：
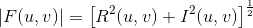
在这里插入图片描述
变换的相角定义如下:

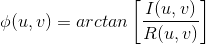
这两个函数可在极坐标形式下用于表示复函数F(u,v)：

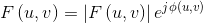
功率谱可以定义为幅度的平方:

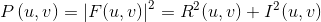
如果f(x,y)是实函数，它的傅立叶变换就是关于原点共轭对称的:

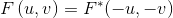
这意味着傅立叶谱也是关于原点对称的:
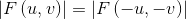
在这里插入图片描述
可以将它直接代入到公式 F(u,v)中:

F(u,v)= F(u+k1,M,v)=F(u,v+ $k_2$ N)= F(u+ $k_1M$ ,v+ $k_2N$ )

其中， $k_1$ 和 $k_2$ 是整数。DFT 在u, v 方向上是无穷周期的，周期由 M和N决定。周期性也是 DFT 逆变换的重要特性：

f(x,y)=f(x+ $k_1M$ ,y)=f(x,y+ $k_2M$ )=f(x+ $k_1M$ ,y+ $k_2N$ )

也就是说，通过傅立叶反变换得到的图像也是无穷周期的。并且，在计算离散傅立叶变换时只计算它的一个周期，即仅处理尺寸为MXN的数组。

（二）在 MATLAB 中计算及观察二维 DFT

在实践中，DFT 及其反变换可以用快速傅立叶变换(FFT)算法实现。一幅图像数组 f 的 FFT 可以在 MATLAB中用函数 fft2 得到，语法如下：

F = fft2(f)

代码编写：

f = imread('D:\数字图像处理\第三章学习\light.png');
F = fft2(f);
subplot(1, 2, 1), imshow(f), title('原图像');
subplot(1, 2, 2), imshow(uint8(real(F))), title('图像数组f的FFT');

代码运行状态如下：

这个函数返回的傅立叶变换，大小仍为 MxN，目前是看不出来什么。

继续操作，使用傅立叶变换滤波时，需要对输入数据进行 0 填充。在这种情况下，语法变为：

F = fft2 (f,P,Q)             %快速傅里叶变换

代码编写如下：

f = imread('D:\数字图像处理\第三章学习\light.png');
F = fft2(f,200,300);
subplot(1, 2, 1), imshow(f), title('原图像');
subplot(1, 2, 2), imshow(uint8(real(F))), title('图像数组f的FFT');       %real获得F的傅里叶变换的实部：

代码运行状态如下：

fft2 对输入图像填充所需数目的 0, 结果大小变为 200x300。

傅立叶谱可以通过使用函数 abs 函数获得：

S = abs(F)

代码编写：

g = imread('D:\数字图像处理\第三章学习\light.png');
f = rgb2gray(g);    %把图像变为灰度图像
F = fft2(f);
S = abs(F);
subplot(1, 2, 1), imshow(g), title('原图像');
subplot(1, 2, 2), imshow(S,[]), title('傅里叶谱');

代码运行状态如下：

图中 4个角上的亮点是周期特性的结果。可以使用函数 fftshift 将变换的原点移动到频域矩形的中心，语法为：

Fc = fftshift(F)

代码编写：

g = imread('D:\数字图像处理\第三章学习\light.png');
f = rgb2gray(g);    %把图像变为灰度图像
F = fft2(f);
Fc = fftshift(F);      %将变换的原点移动到频域矩形的中心
subplot(1, 2, 1), imshow(g), title('原图像');
subplot(1, 2, 2), imshow(abs(Fc),[ ]), title('fftshift居中变换');

代码运行状态如下：

居中后的结果是很明显的。该谱值的范围很大(0 到420 495)，与用 8 位显示相比，中心处的亮度值占支配地位。可通过 log 变换处理这个难点。

代码编写如下：

g = imread('D:\数字图像处理\第三章学习\light.png');
f = rgb2gray(g);    %把图像变为灰度图像
F = fft2(f);
Fc = fftshift(F);         %将变换的原点移动到频域矩形的中心
S2 = log(1+ abs(Fc));      % 对数变换，增强显示视觉效果
subplot(1, 2, 1), imshow(g), title('原图像');
subplot(1, 2, 2), imshow(S2,[ ]), title('log变换处理增强细节');

代码运行状态如下：

可见细节的增加是很明显的。反居中变换函数 ifftshift 的语法形式是：

F = ifftshift(Fc)

代码编写：

g = imread('D:\数字图像处理\第三章学习\light.png');
f = rgb2gray(g);    %把图像变为灰度图像
F1 = fft2(f);
Fc = fftshift(F1);
F = ifftshift(Fc)
subplot(1, 2, 1), imshow(g), title('原图像');
subplot(1, 2, 2), imshow(uint8(real(F))), title('ifftshift反居中变换');

代码运行状态如下：

这个函数也可以用来将初始点在矩形中点的函数变换为中心点在矩形左上角的函数。

（三）频域滤波

3.1基础知识

空(间)域和频(率)域的线性滤波的基础都是卷积定理，可以被写作:
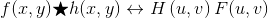
在这里插入图片描述
逆变换为：

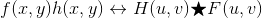
在这里，符号"星号"表示两个函数的卷积，双箭头两边的表达式组成傅立叶变换对。例如, 第一个表达式表明两个空间函数(表达式左侧的项)的卷积可以通过计算两个傅立叶变换函数(表达式的右侧)的乘积的反变换得到。相反，两个空间函数的卷积的正傅立叶变换给出了两个函数傅立叶变换的乘积。

当工作在离散量时，我们知道F和H是周期性的，这意味着在离散频域执行卷积也是周期性的。由于这个原因，用DFT 执行的卷积叫做循环卷积。保证空间和循环卷积给出相同结果的唯一方法是使用适当的 0 填充。

执行未填充的滤波效果，代码编写：

function H = lpfilter(type, M, N, D0, n)
[U, V] = dftuv(M, N);
D = sqrt(U.^2 + V.^2);
switch type
case 'ideal'
   H = double(D <= D0);
case 'btw'
   if nargin == 4
      n = 1; 
   end
   H = 1./(1 + (D./D0).^(2*n));
case 'gaussian'
   H = exp(-(D.^2)./(2*(D0^2)));
otherwise
   error('Unknown filter type.')
end

h = imread('D:\数字图像处理\第三章学习\cat2.jpg');
f = im2double(rgb2gray(h));        %把图像变为灰度图像
[M,N]=size(f);
F = fft2(f);                      %计算傅里叶变换
sig=10;                           %指定高斯低通滤波器的标准偏差
H=lpfilter('gaussian',M,N,sig);   %高斯低通滤波器生成
G=H.*F;                           %将变换乘以滤波函数
g=real(ifft2(G));                 %获得G的傅里叶逆变换实部
figure;
subplot(1, 2, 1), imshow(h), title('原图像');
subplot(1, 2, 2), imshow(g), title('未填充的滤波效果');

代码运行效果如下：

正像我们预计的那样，图像变模糊了，但是注意垂直的边缘没有模糊。

执行已填充的滤波效果，代码编写：

function PQ = paddedsize(AB, CD, PARAM)
if nargin == 1
    PQ = 2*AB;
elseif nargin == 2 && -ischar(CD)
    PQ = AB + CD - 1;
    PQ = 2 * ceil(PQ / 2);
elseif nargin == 2
    m = max(AB);
    P = 2^nextpow2(2*m);
    PQ = [P, P];
elseif (nargin == 3) && strcmp(PARAM, 'pwr2')
    m = max([AB CD]);
    P = 2^nextpow2(2*m);
    PQ = [P, P];
else
    error('Wrong number of inputs.')
end

h = imread('D:\数字图像处理\第三章学习\cat2.jpg');
f = im2double(rgb2gray(h));         %把图像变为灰度图像
PQ = paddedsize(size(f));           %用函数 paddedsize 获得填充参数
Fp = fft2(f,PQ(1),PQ(2));           %得到有填充的傅立叶变换
Hp = lpfilter('gaussian', PQ(1), PQ(2), 2*sig);     %现在滤波器的大小是没有进行填充时的两倍。 
Gp=Hp.*Fp;                          %用滤波器乘以FFT 变换
gp=ifft2(Gp);                       %获得 Gp 的逆 FFT 变换
gpc = gp(1:size(f,1), 1:size(f,2)); 
figure;
subplot(1, 2, 1), imshow(h), title('原图像');
subplot(1, 2, 2), imshow(gpc), title('已填充的滤波效果');

代码运行效果如下：

现在，这个图像有围绕在四周的均匀黑色边界。因此，用这个无限序列与平滑滤波器卷积，将会在图像所有的亮边缘显示灰色的模糊效果。

3.2 DFT 滤波的基本步骤

前面的讨论可以概括为下面几个步骤，其中 f 是被滤波处理的图像，gpc为处理结果，同时假设滤波函数 H与填充后的图像大小相等。

把输入图像变成double类型图像：

f = im2double(rgb2gray(h));

用函数 paddedsize 获得填充参数：

PQ = paddedsize(size(f));

得到有填充的傅立叶变换:

Fp = fft2(f,PQ(1),PQ(2));

用滤波器乘以FFT 变换：

Gp=Hp.*Fp;

获得 Gp 的逆 FFT 变换:

gp=ifft2(Gp);

修剪左上部矩形为原始大小:

gpc = gp(1:size(f,1), 1:size(f,2));

预处理阶段包括确定图像大小，获得填充参数和生成一个滤波函数等，后处理阶段包括计算结果的实部，修剪图像，以及将图像类型的转换。

3.3 频域滤波的M-函数

有一些可用的 M-函数是很方便的，它们可以接收输入图像和滤波函数，处理所有滤波细节，并输出滤波后的结果以及修剪图像。下面的函数可实现这些工作，假定滤波函数已被适当地做了大小排列。在某些应用中，把滤波后的图像变换为与输入相同的类是很有用的；有些时候处理浮点数是必要的。这些函数可以做这些事。

function g = dftfilt(f, H, classout) 
[f, revertClass] = tofloat(f);               %用函数 tofloat 把输入图像变换为浮点图像：
F = fft2(f, size(H, 1), size(H, 2));         %得到有填充的傅立叶变换
g = ifft2(H.*F);                             %获得H.*F的逆FFT变换
g = g(1:size(ff 1), 1:size(f, 2));           %修剪左上部矩形为原始大小
if nargin == 2 || strcmp(classout,'priginal')         %输入参数个数为2
    g = revertClass(g);                      %把滤波过的图像变换为输入图像的类
 elseif strcmp(classout,'fltpoint')          %比较classout是否为fltpoint
   return 
 else
   error('Undefined class for the output image.’)
end

数字图像处理第三章——频域处理（上）

数字图像处理第三章

数字图像处理—频域处理

（一）二维离散傅里叶变换

（二）在 MATLAB 中计算及观察二维 DFT

（三）频域滤波

3.1基础知识

3.2 DFT 滤波的基本步骤

3.3 频域滤波的M-函数

猜你喜欢