简介
在构造kd-tree中,我们需要对方差最大维度上的中位数进行计算。中位数计算方法的好坏一定程度上影响了树的构造时间。要计算中位数,我们一般想到的是将数据进行排序,然后取中间的数。排序算法最快的时间复杂度为O(nlogn)。但是实际上我们要求中位数,不需要将所有数据进行排序,有的排序步骤是无用的。所以有了选择算法,其平均时间复杂度为O(n),最坏时间复杂度为O(n2)。在Rob Hess 的sift源码中,kd-tree使用了一种快速选择算法,能使最坏时间复杂度为O(n)。下面我们将对快速排序算法、选择算法、快速选择算法进行对比介绍。
快速排序
快速排序步骤:
(1)首先设定一个分界值,通过该分界值将数组分成左右两部分。
(2)将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。
(3)重复(1)(2)步骤直至数据不能再划分为止。
第一次排序:
以第一个数为分界值,从左往右找一个比分界值大的数,从右往左找一个比分界值小的数,如果比分界值大的在小的左边,则交换两个数位置。再记录下比分界值小的数的个数,最后将分界值放入对应位置,完成第一次排序。接着对分界值左边和右边的数分别进行递归操作直到完成排序。
递归排序: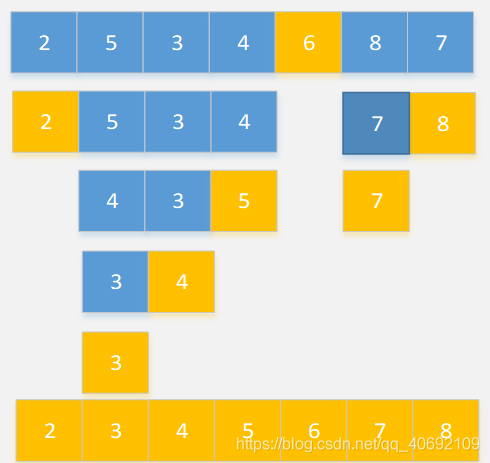
代码如下:
template<typename T>
static void Qsort(T arr[], int low, int high) {
//c++;
if (high <= low) return;
int i = low;
int j = high + 1;
int key = arr[low];
while (true)
{
/*从左向右找比key大的值*/
while (arr[++i] < key)
{
if (i == high) {
break;
}
}
/*从右向左找比key小的值*/
while (arr[--j] > key)
{
if (j == low) {
break;
}
}
if (i >= j) break;
/*交换i,j对应的值*/
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
/*中枢值与j对应值交换*/
int temp = arr[low];
arr[low] = arr[j];
arr[j] = temp;
Qsort(arr, low, j - 1);
Qsort(arr, j + 1, high);
}选择算法
在前面快速排序中,我们确定了6的位置之后,由于我们需要寻找中位数,完全不需要对6右边的数据进行排序,因此有了选择算法。与快速排序一样,我们将输入数组进行递归划分,与快速排序不同的是,快速排序会递归处理划分的两边,而选择只处理划分一边。
橙色为我们需要确定的中间位置的数,黄色为当前作分界值的数,也是一轮比较交换之后能确定位置的数。当我们每次确定位置的数确定的位置在中间位置,那么这个分界值数就是中位数。

代码如下:
template<typename T>
T Select(T arr[], int low, int high, int m) {
//c++;
if (high <= low)
{
return -1;
}
int i = low;
int j = high + 1;
int key = arr[low];
while (true)
{
/*从左向右找比key大的值*/
while (arr[++i] < key)
{
if (i == high) {
break;
}
}
/*从右向左找比key小的值*/
while (arr[--j] > key)
{
if (j == low) {
break;
}
}
if (i >= j) break;
/*交换i,j对应的值*/
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
/*中枢值与j对应值交换*/
int temp = arr[low];
arr[low] = arr[j];
arr[j] = temp;
if (j > m) {
mQsort(arr, low, j - 1, m);
}
if (j < m) {
mQsort(arr, j + 1, high, m));
}
if (j = m) {
return arr[j];
}
}快速选择算法
当输入为逆序是,快速排序和选择算法的时间复杂度都会降为O(n2),为了防止选择算法最坏情况的产生,我们需要使每次确定的数尽可能等分数据,即尽可能接近中位数(在选择排序中,我们选择的为第一个数进行判断)。所以我们不在随机选择一个数据进行划分,而是先寻找一个接近中位数的数据进行划分。
快速选择算法对选择算法在选择划分数据时进行了修改。将输入数组的n个元素划分为n/5组,每组5个元素。首先对每组元素进行插入排序,然后找每组中位数的中位数k,以k对数据进行划分。这样可是划分值k更接近中位数,防止最坏情况发生。
中位数的选取如图所示,黄色为每组选出的中位数,选出之后再对黄色的这些中位数递归调用快速选择算法选择中位数。
伪代码如下:
Select(数组,数组起点,数组终点,中点位置m){
将输入数组的n个元素划分为n/5组,每组5个元素,对每组元素进行插入排序;
Select()递归调用求每组数据中位数的中位数k;
数组内所有点与k比较,小于放它左边,大于放它右边;此时k所在位置为 j;
if(j > m){
return Select(数组,数组起点,j - 1,m);
}
if (j < m){
return Select(数组,j +1,数组终点,m);
}
return arr[m] ;
}
代码如下:
emplate<typename T>
static void insertion_sort(T* array, int n)
{
T k;
int i, j;
for (i = 1; i < n; i++)
{
k = array[i];
j = i - 1;
while (j >= 0 && array[j] > k)
{
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = k;
}
}
template<typename T>
static int partition_array(T* array, int n, T pivot)
{
T tmp;
int p, i, j;
i = -1;
for (j = 0; j < n; j++)
if (array[j] <= pivot)
{
tmp = array[++i];
array[i] = array[j];
array[j] = tmp;
if (array[i] == pivot)
{
p = i;
}
}
array[p] = array[i];
array[i] = pivot;
return i;
}
template<typename T>
T rank_select(T* array, int n, int r)
{
// c++;
T* tmp, med;
int gr_5, gr_tot, rem_elts, i, j;
/* base case */
if (n == 1)
return array[0];
/* divide array into groups of 5 and sort them */
gr_5 = n / 5;
gr_tot = cvCeil(n / 5.0);
rem_elts = n % 5;
tmp = array;
for (i = 0; i < gr_5; i++)
{
insertion_sort(tmp, 5);
tmp += 5;
}
insertion_sort(tmp, rem_elts);
/* recursively find the median of the medians of the groups of 5 */
tmp = (T*)calloc(gr_tot, sizeof(T));
for (i = 0, j = 2; i < gr_5; i++, j += 5)
tmp[i] = array[j];
if (rem_elts)
tmp[i++] = array[n - 1 - rem_elts / 2];
med = rank_select(tmp, i, (i - 1) / 2);
free(tmp);
/* partition around median of medians and recursively select if necessary */
int i2 = 0;
j = partition_array(array, n, med);
if (r == j)
return med;
else if (r < j)
return rank_select(array, j, r);
else
{
array += j + 1;
return rank_select(array, (n - j - 1), (r - j - 1));
}
}速度比较
横坐标为数据量
纵坐标为计算时间
粉色-冒泡排序 O(N2)
红色-快速排序 O(NlogN)
绿色-快速选择算法 O(N)
蓝色-选择算法 O(N)
通过斜率可以清楚看到这些算法的时间复杂度。

从图中可看到选择算法比快速选择算法更快,但是在最坏情况下(逆序输入)可看到如下结果:

这时快速排序和选择算法时间复杂度都变为了O(N2)。(其实逆序输入并不是快速选择算法的最坏情况)
参考:
Rob Hess sift源码