凸包上的DP，WQS二分优化

前言

考炸了CSP，调整调整心态。。。

然后就学了这个地步。

感觉学较为简单的算法真的能够愉悦身心。

参考文献

个题题解

题集：https://www.cnblogs.com/HocRiser/p/9834069.html

关于整点证明的启发虽然我没看懂：https://www.cnblogs.com/CreeperLKF/p/9045491.html

关于最小度限制生成树与WQS二分的区别：https://www.luogu.com.cn/blog/EndSaH/solution-cf125e

例题演示

例题

题目链接

中文题意，自己看吧。。。

从题解出发的讲解

如果你没有思路的话，我可以很负责任的告诉你。

刚开始我也没思路，就连题解需要的前提条件都是我已经证明了题解做法正确性之后才推出的前提条件。

我采用的是克鲁斯卡尔的做法。

我们思考一下，我们要让生成树包含一定量的白边，那么就要改变白边在生成树中的位置，那么我们可以给每条边加上一个权值\(k\)（可以为正，可以为负）。

当然这里需要证明一个东西，就是增加的数字越小，白边选中的也就越多，也许你会说是废话，但是有时候这些东西还是要证明的，感性理解太吃shit了。

首先，对于前面的一条为未选中的白边，\(A->B\)，那么在生成树中肯定有\(A->B\)的一条链。

我们对于其中权值最大的黑边而言（箭头指的边，如果没有的话，那么这个白边不可能被选中），白边的值原本大于黑边，当加完权值后大于最大的黑边的话，那么这条黑边将彻底淘汰，也就是多了一条白边。

可以发现，这个权值\(k\)是整数就够了，不用是小数，如果\(k\)加\(1\)减\(1\)产生了大量白边怎么办呢？后面会讲。

那么我们现在就是要证\(k-1\)的生成树比\(k\)的生成树的白边要多或者相同。

那么也就是对于\(k\)的生成树中，更多的白边取代了黑边，而原本的白边，也不会消失，为什么，因为不可能有白边超过他呀。

同时对于\(k\)越大而言呢，你可以视作其实是黑边的加上\(-k\)，然后证明黑边数量递增就行了。

所以就是正确的了，然后跑完以后只要把生成树的代价减去白边的数量就行了。

那么其实我们就可以通过二分\(k\)值来控制白边的数量。

但是其实还涉及一个问题，什么问题呢？

就是如果有相同权值的白边和黑边，选什么。

那么我们只要在排序优先白边，然后问大于等于就行了。

不过需要注意一个事情，就是什么呢吗，就是白边虽然选的多了，但是其实我们只是来统计数量的，我们最终只选\(need\)个白边，多出的就当选了黑边了，所以每次减去也是\(need*k\)。

当然，你也可以用这个来证明一个事情，就是选不同数量的白边都可以在对应的\(k\)成为最小值。

那么就可以上代码了。

#include<cstdio>
#include<cstring>
#include<algorithm>
#define  N  51000
#define  M  110000
using  namespace  std;
int  fa[N];
int  findfa(int  x)
{
    if(fa[x]==x)return  x;
    return  (fa[x]=findfa(fa[x]));
}
struct  node
{
    int  x,y,c,type;
}a[M];int  len,dep/*白边的系数*/,need;
inline  void  ins(int  x,int  y,int  c,int  type){len++;a[len].x=x;a[len].y=y;a[len].c=c;a[len].type=type;}
inline  bool  cmp(node  x,node  y){return  (x.c+x.type*dep)==(y.c+y.type*dep)?x.type>y.type:(x.c+x.type*dep)<(y.c+y.type*dep);}
int  n,m,ans,zans;
int  check()
{
    sort(a+1,a+m+1,cmp);
    for(int  i=1;i<=n;i++)fa[i]=i;
    int  cnt=0,bai=0;ans=0;
    for(int  i=1;i<=m;i++)
    {
        int  x=a[i].x,y=a[i].y;
        int  tx=findfa(x),ty=findfa(y);
        if(tx!=ty)
        {
            fa[tx]=ty;
            cnt++;ans+=a[i].c;
            if(a[i].type)bai++,ans+=dep;
            if(cnt==n-1)return  bai;
        }
    }
}
int  main()
{
//  freopen("tree7.in","r",stdin);
    scanf("%d%d%d",&n,&m,&need);
    for(int  i=1;i<=m;i++)
    {
        int  x,y,c,type;scanf("%d%d%d%d",&x,&y,&c,&type);
        ins(x+1,y+1,c,type^1);
    }
    int  l=-100,r=100;
    while(l<=r)
    {
        dep=(l+r)/2;
        int  tt=0;
        if((tt=check())>=need)
        {
            
            zans=ans-need*dep,l=dep+1;
        }
        else  r=dep-1;
    }
    printf("%d\n",zans);
    return  0;
}

相信还是有很多的人不懂，但是可以跳到下个专题直接学习WQS二分，相信你会灵光一闪的。

正式讲解WQS优化

适用范围

对于题目中要求一定要选到多少个什么东西这种题目。

如果对于\(f(j)\)，表示的是刚好选到了\(j\)个的代价。

然后\(f\)的函数图像是一个上凸包（或者下凸包）：

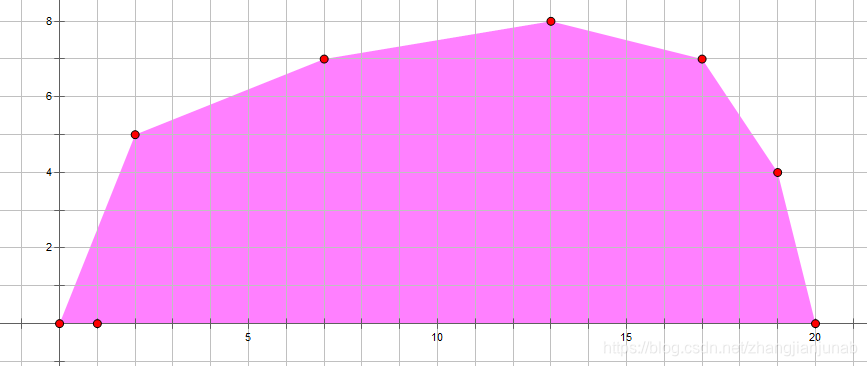
那么就可以使用WQS二分啦。

别看就两点，但是能用的题目可是少之又少的。

讲解加证明

而且也会有不少的人有疑惑，凸包不应该是三分吗，怎么又变成了二分了。

下面的全部采用上凸包，就是上面的那张图。

这里就用用到凸包的一个特别神仙的性质，就是当在递增的区域中\(f(i)-f(i-1)<=f(i-1)-f(i-2)\)，下降就是\(f(i)-f(i+1)>=f(i+1)-f(i+2)\)。为什么看图都看的出来吧，如果不是他就不是凸包了。

我们尝试给\(f(i)\)加上\(i*k\)。

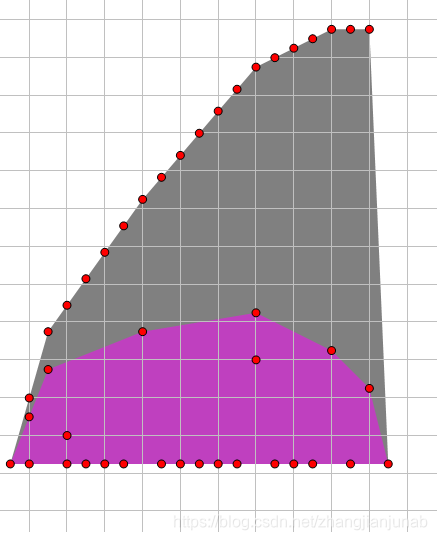
然后得到了这个图像，我们可以继续证明新图像(灰色)也是凸包（也就是满足凸包的性质）。

当\(k>0\)的时候（\(k<0\)一样的证明）：

其实对于两点之差就只是\(+k\)，所以还是凸包，但是最大值的位置却右移了！！！！

于是我们发现了一个事情，就是\(k\)越大，最大值的横坐标越大，所以就可以二分\(k\)值，来找到对应的最大值了。

为什么横坐标越大呢，其实最大值的横坐标\(i\)就是最大的且满足\(f(i)-f(i-1)+k>=0\)的地方，所以就是递增的啦。

而对于\(k\)越小，就是横坐标越小。

其实满足这个性质的，他的图像也就是凸包了，比如\(Tree\)这道题目，就可以发现其满足这个性质，然后倒退出他的图像是个凸包。

那么我们现在只需要解决两个问题了。

当坐标都是整数的时候二分的k可以只是整数吗

这个时候我们发现当\(f(i+1)-f(i)=-k\)（\(i\)在递减的区域上），那么这个时候\(i\)是整个凸包的最大值。

那么我们发现两点\(y\)坐标之差肯定是整数，那么\(k\)是整数就够了。

当然，坐标是小数就不能这么做了

多个最大值的怎么办

经常会发生一个事情，就是有多个最大值相同，这个时候其实我们在\(check\)的过程中可以默认取到最大的，然后在二分中找到横坐标大于最接近于\(need\)的\(k\)，那么我们所需要的位置肯定是在\(+k\)的时候最大，因为\(+k-1\)的位置小于\(need\)，所以这个位置当最大值的情况只可能在\(+k\)的时候最大了。

当然我之所以不会做\(WQS\)二分套\(WQS\)二分的题目也就是一直搞不懂两个之间的最大值要怎么判断

小结

个人感觉WQS最难的地方就是证明这个图像是否是个凸包了。

但是去网络上看会发现其实WQS有很多专业的术语，可以我是看了做法然后自证的QAQ。

练习

个人感觉WQS最有用的地方就是可以去做有限制的生成树了吧。

当然WQS最牛逼的用处就是优化DP，如果DP优化完后还要用四边形不等式的话，你就可以切黑题了，可惜我不会四边形不等式优化。

1

题目

双倍经验

天哪！第二道题我当时还证不出凸包，然后后面看了一下以前这道题，我以前是怎么证凸包来着？不会是抽象理解吧。

这两道题目如果直接去证明他是个凸包的话，如果吃了屎似的，但是如果你把题目转化一下，排序做差分，就变成了求选\(m\)不相邻的数字之和最小。

那么我们很快想出了\(DP\)状态，\(f[i][j]\)表示到第\(i\)个数字选了\(j\)个数字的答案。

然后我们就可以证明\(g(i)=f[n][i]\)这个函数是凸包了。

其实不是不转化就不能证，只是好像，感觉第一道题在做的时候压根就没有考虑什么是凸包这个问题。

我们可以发现，每次我们都可以去选择一些数字，但是我们其实发现了一些问题就是选这个数字可能需要一些数字的让步，让他们去选其他数字，甚至还会去选比以前选的数字小的数字！！！！

凸包证明，不会

#include<cstdio>
#include<cstring>
#define  N  110000
using  namespace  std;
typedef  long  long  LL;
struct  node
{
    LL  f;
    LL  mat;/*匹配数*/
}dp[N][2]/*0选，1不选*/;
LL  n,m,a[N];
node  check(LL  x)
{
    for(LL  i=2;i<=n;i++)
    {
        dp[i][0].f=dp[i-1][1].f+a[i]-a[i-1]+x;dp[i][0].mat=dp[i-1][1].mat+1;
        //选
        if(dp[i-1][0].f<dp[i-1][1].f  ||  (dp[i-1][0].f==dp[i-1][1].f  &&  dp[i-1][0].mat>dp[i-1][1].mat))dp[i][1]=dp[i-1][0];
        else  dp[i][1]=dp[i-1][1];
        //不选 
    }
    if(dp[n][0].f<dp[n][1].f  ||  (dp[n][0].f==dp[n][1].f  &&  dp[n][0].mat>dp[n][1].mat))return  dp[n][0];
    else  return  dp[n][1];
}
int  main()
{
    scanf("%d%d",&n,&m);
    for(LL  i=1;i<=n;i++)scanf("%d",&a[i]);
    LL  l=a[1]-a[n]-1,r=0,mid;
    node  ans;
    while(l<=r)
    {
        mid=(r-l)/2+l;
        node  now=check(mid);
        if(now.mat>=m)ans=now,ans.f-=(LL)mid*m,l=mid+1;
        else  r=mid-1;
    }
    printf("%lld\n",ans.f);
    return  0;
}

差不多的题目

只不过需要设\(f[i][0/1][0/1]\)表示到第\(i\)个数字，第一个数字选了没选，第\(i\)个数字选了没选的情况。

其实就是刷题的时候没看到。

练习2

黑题！！！！

这道题目我差点就做出来了QAQ。

其实如果你知道是\(WQS\)还是比较好做的。

首先们可以发现其实题目要求就是选出在树上的\(k+1\)条点不重复的路径之和的最大值。

那么我们就可以设\(f[i][k]\)表示表示到了第\(i\)点选了\(k\)条路径的情况。

但是我们发现我们没办法拼接路径！！！！

所以我们重制一下\(DP\)状态就是\(f[i][k][0/1/2]\)的情况，也就是第\(i\)个点没在路径上的情况、点\(i\)在一条未成形的路径上，且在路径上的度为\(1/2\)的情况，未成形的意思就是没计入\(k\)的数量中。其实我个人觉得计入了也可以做。

然后\(DP\)方程自己推吧，应该不难了。

那么我们现在要证的是什么呢？

也就是\(g(i)=max(f[1][i][0],f[1][i][1],f[1][i][2])\)（\(1\)为根节点）是一个凸包。

那么这个我们很愉快的交给了读者自证。(雾

然后我们只需要在每次把未成形的路径在成形的时候\(+k\)，然后二分\(k\)就行了。

#include<cstdio>
#include<cstring>
#include<algorithm>
#define  N  310000
#define  NN  610000
using  namespace  std;
typedef  long  long  LL;
template  <class  T>
inline  T  mymin(T  x,T  y){return  x<y?x:y;}
template  <class  T>
inline  T  mymax(T  x,T  y){return  x>y?x:y;}
//DP数组 
struct  node
{
    LL  sh;//表示分的段数，1,2不算一段 
    LL  x;//表示的是保留一条边减去保留两条然后加上到父亲的边权。 
    node(LL  xx=0,LL  yy=0){x=xx;sh=yy;}
}f[N][3];
inline  bool  operator<(node  x,node  y){return  x.x!=y.x?(x.x<y.x):(x.sh<y.sh);}
inline  bool  operator>(node  x,node  y){return  x.x!=y.x?(x.x>y.x):(x.sh>y.sh);}
inline  node  operator+(node  x,node  y){return  node(x.x+y.x,x.sh+y.sh);}
struct  bian
{
    LL  y,next;
    LL  c;
}a[NN];LL  len=1,last[N];
void  ins(LL  x,LL  y,LL  c){len++;a[len].y=y;a[len].c=c;a[len].next=last[x];last[x]=len;}
LL  fu/*表示每次断边的附加权值*/,top;
bool  v[N];//是否有被查到 
node  an;
void  dfs(LL  x,LL  fa)//处理出最简单的DP 
{
    if(x==6)
    {
        x++;
        x--;
    }
    f[x][0]=f[x][2]=node(0,0);f[x][1]=node((LL)-9999999999999999,0/*自己自成一段*/);
    for(LL  k=last[x];k;k=a[k].next)
    {
        LL  y=a[k].y;
        if(y!=fa)dfs(y,x);//处理出子树信息 
    }
    for(LL  k=last[x];k;k=a[k].next)
    {
        LL  y=a[k].y;
        if(y!=fa)
        {
            node  no1=mymax(f[y][0],f[y][1]);no1.x+=a[k].c;//使用这条边的最大值 
            node  no2=mymax(f[y][1],f[y][2]);no2=mymax(node(no2.x+fu,no2.sh+1)/*断边*/,f[y][0]/*不断边，也不使用*/);//表示不使用这条边，割掉，或者直接不用 
            //询问其能不能多添加一条边 
            f[x][2]=mymax(f[x][2]+no2,f[x][1]+no1);
            f[x][1]=mymax(f[x][1]+no2,f[x][0]+no1/*表示使用这条边*/); 
            f[x][0]=f[x][0]+no2;//表示使用其中的0条边。 
        }
    }
}
LL  n,m;//表示点数和边数。 
bool  check()
{
    dfs(1,0);//表示遍历1所在的子树。
    f[1][1].sh++;f[1][2].sh++;
    f[1][1].x+=fu;f[1][2].x+=fu;
    an=mymax(f[1][0],mymax(f[1][1],f[1][2]));
    return  an.sh>=m;
}
int  main()
{
//  freopen("1.in","r",stdin);
//  freopen("1.out","w",stdout);
    scanf("%lld%lld",&n,&m);m++;
    for(LL  i=1;i<n;i++)
    {
        LL  x,y;LL  c;scanf("%lld%lld%lld",&x,&y,&c);
        ins(x,y,c);ins(y,x,c);
    }
    LL  l=-1e13,r=1e13,zans=0;
    while(l<=r)
    {
        fu=(l+r)/2;
        if(check())
        {
            zans=an.x-(LL)m*fu;
            r=fu-1;
        }
        else  l=fu+1;
    }
    printf("%lld\n",zans);
    return  0;
}

其实我很好奇nlog的代码是怎么跑到了1min的。

坑

1. 补练习1和练习2的凸包证明