非线性方程的数值解法
逐步搜索法
设单值连续函数f(x)在有根区间[a,b],不妨假定f(a)<0,从x0=a出发,按预定步长h(譬如取h=(b-a)/N,N为正整数),一步一步地向右跨,每跨一 步进行一 次根的“搜索”,即查点xk=a+kh, k=1, 2, …上的函数值f(x})的符号,一 旦发现xk处与a处函数值异号,f(xk)>0,则可确定一一个缩小了的有根区间[xk-1,xk],其宽度等于预定的步长h。特别地可能有f(xk)=0,这时xk即为所求的根。
区间二分法
给定精确度ε,用二分法求函数零点近似值的步骤为:
确定区间[a,b],验证f(a). f(b)<0;
令c=(a+b)/2,计算f©:若f©=0, 则c就是函数的零点;
若f(a)f©<0,则令b=c (此时零点x。∈(a,c));
若f©. f(b)<0,则令a=c (此时零点x∈(c,b)).;
判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a或b (或是区间(a,b)内任个一数);否则重复上一步。
例如:用二分法求f(x)=2*+x-2的零点时,首先由f(0)<0, f(1)>0,可取区间[0,1].再计算1/2处的函数值,得f(1/2)<0,于是零点在(1/2,1)之间,在计算f(3/4)的值,。。。。。,依次推导下去,直到找到零点或零点的接近值
迭代法
迭代法是一种逐次逼近的方法,它用某个固定公式反复校准根的近似值,使之逐步精确,最后得到满足精确要求的结果。
对非线性方程,利用递推关系式,从 开始依次计算,来逼近方程的根的方法,若仅与有关,即,则称此迭代法为单步迭代法,一般称为多步迭代法;
对于线性方程组,由关系 从开始依次计算来过近方程的解的方法。若对某一正整数,当时,与k无关,称该迭代法为定常迭代法,否则称之为非定常迭代法。
一般可以做如下定义:对于给定的线性方程组(这里的x、B、f同为矩阵,任意线性方程组都可以变换成此形式),用公式(代表迭代k次得到的x,初始时k=0)逐步带入求近似解的方法称为迭代法(或称一阶定常迭代法)。如果存在,记为x*,称此迭代法收敛。显然x*就是此方程组的解,否则称为迭代法发散。
1.区间收敛性
2.局部收敛性
3.全局收敛性
牛顿迭代法
牛顿迭代公式:
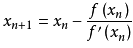
牛顿下山法:
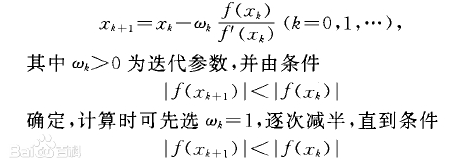
迭代法的解题思路:
一、确定迭代变量
二、建立迭代关系式
三、对迭代过程进行控制
弦截法
1.单点弦法
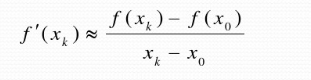
得到如下公式:
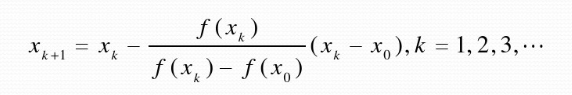
给定初值x。,x1,称公式为单点弦截法
单点弦截法具有线性收敛。
2.双点弦截法:
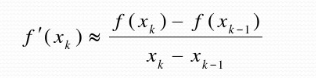
得到如下公式:
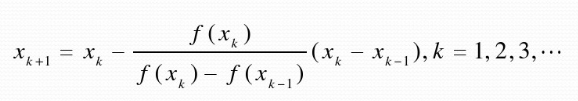
给定初值x。,x1,称公式为双点弦截法双
点弦截法具有1.618阶收敛。
