机器学习（回归三）——线性回归-多项式扩展

概述

前两篇博客介绍的是线性回归，线性回归的一个问题是有可能出现欠拟合现象，因为它求的是具有最小均方误差的无偏估计。显而易见，如果模型欠拟合将不能取得最好的预测效果。所以有些方法允许在估计中引入一些偏差，从而降低预测的均方误差。其中的一个方法是本文的多项式扩展，还有一个是后续的博客会介绍的局部加权线性回归（Locally Weighted Linear Regression，LWLR）。在正式介绍多项式扩展之前，先来看一张对比图

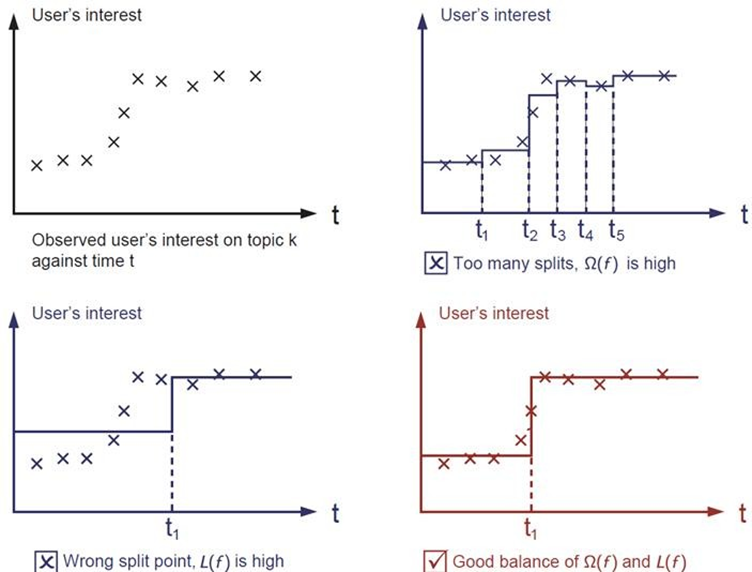
图1，是真实的样本数据，要做的是找到拟合这些点的线。
图2，我们可以把这些点分成不同的区间段，区间段如果选的比较小，两个点一段，均值作为预测值。甚至还可以更小，小到一个点一段，类似于微分的思想。这样肯定会很好的拟合这些样本。
图3，如果选的区间段的跨度比较大，还以均值为预测值，会发现此时的误差会特别大。
上面说的L(f)是预测值与实际值之间的差值，是期望误差。Ω(f)表示方差误差，指复杂度。error = Ω(f) + L(f)，实际来讲不仅仅是降低期望误差，而是二者结合的一个最优。也就是图4的效果。
换句话说，图2是过拟合，图3是欠拟合，图4是比较理想的结果。

就像上图，现实中的样本数据往往都是非线性的，如果能直接找到曲线去拟合，那往往效果会更好。前两篇博客介绍的是线性回归，线性回归针对的是θ而言的，即 $θ_j$ 的最高次项是1次。对于样本本身而言，样本可以是非线性的也就是说最终得到的函数f:x->y；函数f(x)可以是非线性的，比如：曲线等。

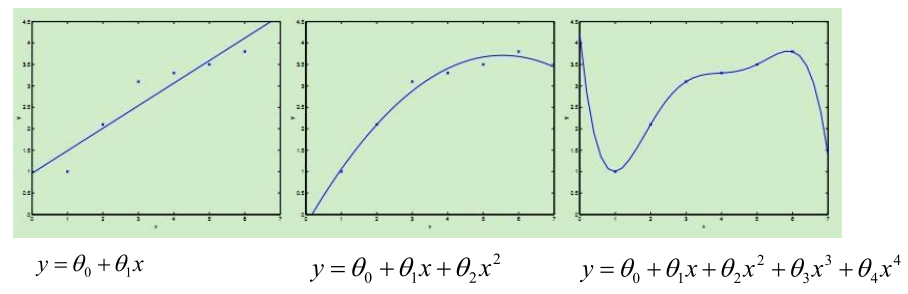
很显然，如果用直线去拟合这种曲线的情况，结果会很不理想，后面的两张图的拟合效果好很多。这就是我们本文提到的多项式扩展。

代码

这里依然使用前面的“家庭用电预测”的样本数据，通过代码看一下时间与电压的多项式关系。

# 引入所需要的全部包
import sklearn
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
import time


# 创建一个时间字符串格式化字符串
def date_format(dt):
    import time
    t = time.strptime(' '.join(dt), '%d/%m/%Y %H:%M:%S')
    return (t.tm_year, t.tm_mon, t.tm_mday, t.tm_hour, t.tm_min, t.tm_sec)


## 设置字符集，防止中文乱码
mpl.rcParams['font.sans-serif']=[u'simHei']
mpl.rcPar
ams['axes.unicode_minus']=False


# 加载数据
path = 'datas\household_power_consumption_200.txt' ## 200行数据
path = 'datas\household_power_consumption_1000.txt' ## 1000行数据
df = pd.read_csv(path, sep=';', low_memory=False)

# 日期、时间、有功功率、无功功率、电压、电流、厨房用电功率、洗衣服用电功率、热水器用电功率
names2=df.columns
names=['Date', 'Time', 'Global_active_power', 'Global_reactive_power', 'Voltage', 'Global_intensity', 'Sub_metering_1', 'Sub_metering_2', 'Sub_metering_3']

# 异常数据处理(异常数据过滤)
new_df = df.replace('?', np.nan)
datas = new_df.dropna(axis=0,how = 'any') # 只要有数据为空，就进行删除操作


## 时间和电压之间的关系(Linear)
# 获取x和y变量, 并将时间转换为数值型连续变量
X = datas[names[0:2]]
X = X.apply(lambda x: pd.Series(date_format(x)), axis=1)
Y = datas[names[4]].values

# 对数据集进行测试集合训练集划分 
X_train,X_test,Y_train,Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)

# 数据标准化
ss = StandardScaler()
X_train = ss.fit_transform(X_train) # 训练并转换
X_test = ss.transform(X_test) ## 直接使用在模型构建数据上进行一个数据标准化操作 

# 模型训练
lr = LinearRegression()
lr.fit(X_train, Y_train) ## 训练模型

# 模型校验
y_predict = lr.predict(X_test) ## 预测结果

# 模型效果
print("准确率:",lr.score(X_test, Y_test))

## 预测值和实际值画图比较
t=np.arange(len(X_test))
plt.figure(facecolor='w')
plt.plot(t, Y_test, 'r-', linewidth=2, label=u'真实值')
plt.plot(t, y_predict, 'g-', linewidth=2, label=u'预测值')
plt.legend(loc = 'lower right')
plt.title(u"线性回归预测时间和功率之间的关系", fontsize=20)
plt.grid(b=True)#网格
plt.show()

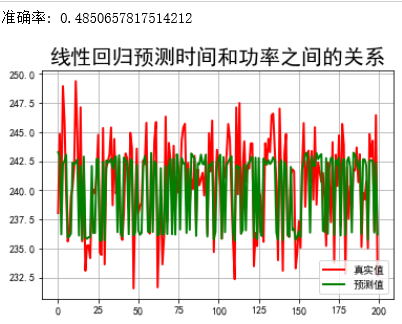
发现：时间和功能之间的关系，不是那的契合，就是说找的这条直线没法很好拟合样本点的。那样本点是不是曲线形式，我们可不可以进行一下扩展？下面就采用了多项式扩展。
多项式扩展：将特征与特征之间进行整合，从而形成新的特征的一个过程；从数学空间上来讲，就是将低维度空间的点映射到高维度空间中。（比如说一维，平方后，就变成了二维。映射到高维之后，数据会更分散，一些特性就更容易体现出来）属于特征工程的一种操作。
作用：通过多项式扩展后，我们可以提高模型的准确率/效果。

## 时间和电压之间的关系(Linear-多项式)
# Pipeline：管道的意思，讲多个操作合并成为一个操作
# Pipleline总可以给定多个不同的操作，给定每个不同操作的名称即可，执行的时候，按照从前到后的顺序执行
# Pipleline对象在执行的过程中，当调用某个方法的时候，会调用对应过程的对应对象的对应方法
# eg：在下面这个案例中，调用了fit方法，
# 那么对数据调用第一步操作：PolynomialFeatures的fit_transform方法对数据进行转换并构建模型
# 然后对转换之后的数据调用第二步操作: LinearRegression的fit方法构建模型
# eg: 在下面这个案例中，调用了predict方法，
# 那么对数据调用第一步操作：PolynomialFeatures的transform方法对数据进行转换
# 然后对转换之后的数据调用第二步操作: LinearRegression的predict方法进行预测
models = [
    Pipeline([
            ('Poly', PolynomialFeatures()), # 给定进行多项式扩展操作， 第一个操作：多项式扩展
            ('Linear', LinearRegression(fit_intercept=False)) # 第二个操作，线性回归
        ])
]

注：这里引入了Pipeline，管道的意思。之前每写都先fit，再transform。通过管道就可以把他们放到一起。

• Poly表示名字，是自定义的，这一行属于第一步，也就是进行多项式扩展；
• Linear也是表示名字，是自定义，这一行属于第二步，也就是进行线性回归。

model = models[0]
# 获取x和y变量, 并将时间转换为数值型连续变量
X = datas[names[0:2]]
X = X.apply(lambda x: pd.Series(date_format(x)), axis=1)
Y = datas[names[4]]

# 对数据集进行测试集合训练集划分
X_train,X_test,Y_train,Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)

# 数据标准化
ss = StandardScaler()
X_train = ss.fit_transform(X_train) # 训练并转换
X_test = ss.transform(X_test) ## 直接使用在模型构建数据上进行一个数据标准化操作 

# 模型训练
t=np.arange(len(X_test))
N = 5
d_pool = np.arange(1,N,1) # 阶

注：阶，即表示扩展后的多项式的最高次

m = d_pool.size
clrs = [] # 颜色
for c in np.linspace(16711680, 255, m):
    clrs.append('#%06x' % int(c))
line_width = 3

plt.figure(figsize=(12,6), facecolor='w')#创建一个绘图窗口，设置大小，设置颜色
#下面是对阶数的迭代
for i,d in enumerate(d_pool):
    plt.subplot(N-1,1,i+1)
    plt.plot(t, Y_test, 'r-', label=u'真实值', ms=10, zorder=N)
    ### 设置管道对象中的参数值，Poly是在管道对象中定义的操作名称， 后面跟参数名称；中间是两个下划线
    model.set_params(Poly__degree=d) ## 设置多项式的阶乘
    model.fit(X_train, Y_train) # 模型训练
    # Linear是管道中定义的操作名称
    # 获取线性回归算法模型对象
    lin = model.get_params()['Linear']
    output = u'%d阶，系数为：' % d
    # 判断lin对象中是否有对应的属性
    if hasattr(lin, 'alpha_'):
        idx = output.find(u'系数')
        output = output[:idx] + (u'alpha=%.6f, ' % lin.alpha_) + output[idx:]
    if hasattr(lin, 'l1_ratio_'):
        idx = output.find(u'系数')
        output = output[:idx] + (u'l1_ratio=%.6f, ' % lin.l1_ratio_) + output[idx:]
    print (output, lin.coef_.ravel())
    
    # 模型结果预测
    y_hat = model.predict(X_test)
    # 计算评估值
    s = model.score(X_test, Y_test)
    
    # 画图
    z = N - 1 if (d == 2) else 0
    label = u'%d阶, 准确率=%.3f' % (d,s)
    plt.plot(t, y_hat, color=clrs[i], lw=line_width, alpha=0.75, label=label, zorder=z)
    plt.legend(loc = 'upper left')
    plt.grid(True)
    plt.ylabel(u'%d阶结果' % d, fontsize=12)

## 预测值和实际值画图比较
plt.suptitle(u"线性回归预测时间和功率之间的多项式关系", fontsize=20)
plt.grid(b=True)
plt.show()

看一下输出的参数：
1阶，系数为： [2.39926650e+02 0.00000000e+00 0.00000000e+00 3.97781449e+00 8.73334650e-01 1.70647992e-01 0.00000000e+00]
2阶，系数为： [ 1.23998300e+02 3.55271368e-14 -7.81597009e-14 5.34497071e+01 2.95068077e+00 2.69407641e-01 -5.32907052e-15 -3.55271368e-15 8.88178420e-16 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 1.02461452e+02 -2.50100464e+01 -5.18469319e-01 0.00000000e+00 -1.02427364e+01 -4.65982219e-01 0.00000000e+00 -3.55472266e-02 0.00000000e+00 .00000000e+00]
3阶，系数为： [ 1.06303324e+12 -7.52773669e+11 2.12816760e+12 -9.53433863e+12 1.50224363e+11 1.24753680e+11 -2.10445177e+11 -2.86373371e+11 -2.73949767e+11 1.63670539e+11 5.97002023e+10 -2.79408605e+11 -3.55726203e+11 -2.59005902e+11 6.79712021e+10 -1.44760428e+10 5.20112328e+10 -9.76562500e-04 2.60610968e+12 -6.05309076e+10 -5.02678348e+10 0.00000000e+00 1.10827637e+00 3.45336914e-01 0.00000000e+00 5.85937500e-03 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 9.10600353e+12 -1.50224363e+11 -1.24753680e+11 0.00000000e+00 -6.41564941e+00 -6.71470642e-01 0.00000000e+00 -1.84478760e-01 0.00000000e+00 0.00000000e+00 4.48028564e+00 2.57629395e-01 0.00000000e+00 -2.65136719e-01 0.00000000e+00 0.00000000e+00 -2.44018555e-01 0.00000000e+00 0.00000000e+00 0.00000000e+00]
4阶，系数为： [ 1.98236950e+13 -6.36266368e+12 -8.19197778e+11 -2.41835460e+13 2.40054791e+12 1.10773332e+12 2.52245897e+12 2.26093380e+12 -4.64598235e+11 -3.10328767e+11 6.98913673e+11 9.69576533e+11 3.36682879e+11 5.31213939e+11 -1.93230766e+11 -7.71628230e+11 3.76054179e+11 1.38354357e+11 5.03666951e+12 -1.14372116e+13 -6.42706951e+11 -1.04958920e+11 9.69966926e+12 2.54696605e+11 -1.21838302e+11 5.77387250e+12 4.40390380e+10 -1.45775272e+10 -1.40971612e+10 -5.91093717e+08 2.89672374e+07 5.29743161e+06 -7.99508243e+05 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 8.80822476e+12 1.81817615e+12 -1.02861244e+12 0.00000000e+00 -3.90835262e+12 -1.02626607e+11 0.00000000e+00 -2.32650507e+12 0.00000000e+00 0.00000000e+00 -1.53422852e+01 -2.18774414e+00 0.00000000e+00 -5.88867188e-01 0.00000000e+00 0.00000000e+00 -2.44140625e-01 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 -1.83344615e+13 1.04699427e+13 1.96360556e+11 0.00000000e+00 -9.69966926e+12 -2.54696605e+11 0.00000000e+00 -5.77387250e+12 0.00000000e+00 0.00000000e+00 1.53059082e+01 -6.72119141e+00 0.00000000e+00 -2.19726562e-01 0.00000000e+00 0.00000000e+00 3.61328125e-02 0.00000000e+00 0.00000000e+00 0.00000000e+00 -3.05761719e+00 -3.54296875e+00 0.00000000e+00 -4.14062500e-01 0.00000000e+00 0.00000000e+00 2.08007812e-01 0.00000000e+00 0.00000000e+00 0.00000000e+00 -2.53906250e-02 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00]

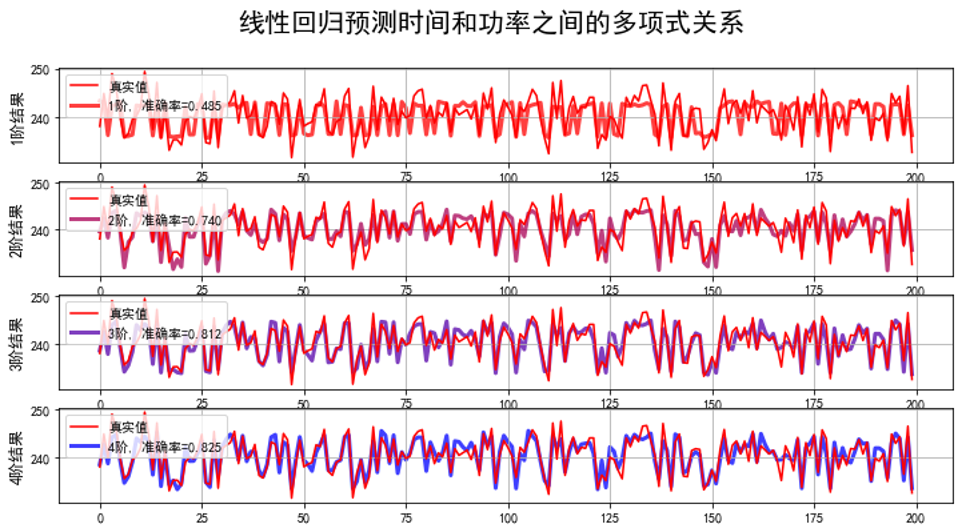
发现：随着阶数增加，准确率在提高。通过多项式扩展能进行很好的拟合

分析

再结合下面一张简化的图，来看一下数据更深层的内容。

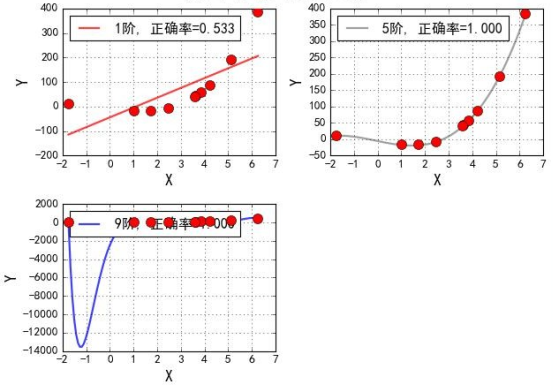
对应的系数：

图中红色的点是样本点，如果用线来拟合的话，近似一条二次函数曲线，而做线性回归，找的是直线，直线和实际分布就不太拟合。通过提高阶数，能对数据进行很好的拟合（图2），但当阶数特别大时（图3），出现了很大的拐线。其实这是出现了严重的过拟合。
过拟合：如果模型在训练集上效果非常好，而在测试集上效果不好，那么认为这个时候存在过拟合的情况，多项式扩展的时候，如果指定的阶数比较大，那么有可能导致过拟合。从线性回归模型中来讲，我们认为训练出来的模型参数值越大，就表示越存在过拟合的情况。（对于过拟合的情况该如何解决，最常用的就是正则化，也就是加入惩罚项，详情内容，下篇博客会介绍）
也就是越复杂，越会出现过拟合。

• 对于线性回归，可能就是参数过多（阶数过大、参数值比较大）
• 对于决策树，就是叶子节点过多
• …

换一个角度来说：
在线性回归中，我们可以通过多项式扩展将低维度的数据扩展成为高维度的数据，从而可以使用线性回归模型来解决问题。也就是说对于二维空间中不是线性可分的数据，将其映射到高维空间中后，变成了线性可分的数据。
两维线性模型:
$h_θ (x_1,x_2 )=θ_0+θ_1 x_1+θ_2 x_2 \\ (x_1,x_2 ) \underrightarrow{多项式扩展} (x_1,x_2,x_1^2,x_2^2,x_1 x_2)$
五维线性模型:
$h_θ (x_1,x_2 )=θ_0+θ_1 x_1+θ_2 x_2+θ_3 x_1^2+θ_4 x_2^2+θ_5 x_1 x_2 \\ \underrightarrow{等价} h_θ (x_1,x_2 )=θ_0+θ_1 z_1+θ_2 z_2+θ_3 z_3+θ_4 z_4+θ_5 z_5$
通过等价变化后，可以看出，从本质上讲，多项式拟合也是一个线性模型。经过上面的分析可以知道，多项式拟合其实是两个过程：

1. 对原始特征向量 x 做多项式特征生成，得到新的特征z
2. 对新的特征 z 做线性回归

其实多项式扩展的这种方法稍想一下就会发现，除了可能的过拟合的问题之外还有：
在最初的例子里做了一个二阶多项式的转换，对一个二维空间做映射，选择的新空间是原始空间的所有一阶和二阶的组合，得到了5个维度；如果原始空间是三维，那么我们会得到9维的新空间；如果原始空间是n维，那么我们会得到一个n(n+3)/2 维的新空间；这个数目是呈爆炸性增长的，这给计算带来了非常大的困难。（SVM对于非线性可分就是用的升维的方式，只不过采用的是更有效的核函数）

总结

事实上，线性回归就是特殊的多项式回归，这很好理解，最后，我想说的是，不考虑过拟合之类的问题，理论上来说，多项式回归应该是可以拟合任何的数据的，因为我们有泰勒定理，任意的函数都可以通过泰勒级数逼近，或许我们构建的多项式过于复杂，有很多项是不需要的（因为多项式回归必须把同一次项的所有情况都要考虑，比如两个特征的三次多项式，只要是特征的幂是三就需要称为多项式的项，而不仅仅是每个特征的一二三次幂），但是我们也要知道，在训练模型的过程中，对数据影响不大的项的参数是会最终趋于零的，所以不考虑计算量、过拟合等问题，哪怕我们只用多项式回归这个方法，也足够拟合任意的数据集了。