事情是这样的,昨天,有个小伙伴在群里发了个题目,让大家回答,题目本身是很简单的,如下:
财迷有多少钱?
有一个财迷总想使自己的钱成倍增长,一天他在一座桥上碰见了一个老人,老人说:”你只要走过这座桥再回来,你身上的钱就会增加一倍,但你每走一个来回要给我32个铜板。“财迷觉得合算,就同意了。他走过桥又走回来,身上的钱果然增加了一倍,他高兴地给了老人32个铜板。这样走完第五个来回,财迷身上最后的32个铜板都给了老人,一个也没剩。财迷身上原来有多少个铜板?
怎样,题目本身简单吧?没错!大家第一感觉就是逆推,并且很快就能逆推出答案:
第5次走完以后 0 走之前(0 + 32 )/2 = 16
第4次走完以后 16 走之前(16 + 32 )/2 = 24
第3次走完以后 24 走之前(24 + 32 )/2 = 28
第2次走完以后 28 走之前(28 + 32 )/2 = 30
第1次走完以后 30 走之前(30 + 32 )/2 = 31
这种方式是一眼就能得出的方法,写成程序也很简单:
int f(int x) //输入走之后有多少钱计算走之前有多少钱
{
return (x + 32) / 2;
}
int main()
{
int x = 0;
int count_max = 5;
for(int i = 0;i < count_max;i++)
{
x = f(x);
}
cout << "原来有 " << x << " 个铜板" << endl;
system("pause"):
return 0;
}
但是,慢着,这边出现了循环....而且循环里面只是一个式子,那么我们能不能给他抽象成一个通项公式呢?
是可以的!
我们将次数抽象出来,n次以后用完铜板,那么
n == 1 :
a0 * 2 - 32 = 0 //a0 代表进入第1次时候的初始铜板
a0 = 32 / 2
n == 2 :
a1 * 2 - 32 = 0
a0 * 2 - 32 = a1
结合上面两个式子 : (a0 * 2 - 32) * 2 - 32 = 0 => a0 = 32/2 + 32/4
n == 3 :
a2 * 2 - 32 = 0
a1 * 2 - 32 = a2
a0 * 2 - 32 = a1
结合上面三个式子 : ((a0 * 2 - 32) * 2 - 32 ) * 2 - 32 = 0 => a0 = 32/2 + 32/4 + 32/8
...
现在 上面似乎有了规律:
若n次以后用完铜板
则 a0 = 32/(2^1)+ 32/(2^2) + 32/(2^3) ... 32/(2^n)
进一步化简为
a0 = 32*(1/(2^1)+ 1/(2^2) + 1/(2^3) ... 1/(2^n))
进一步化简为
进一步化简为
a0 = 32*( 2^n - 1/ 2^n )
嘿嘿,这样就出来了一个简单的通项公式可以很方便的求出初始有多少钱了!再把每次要付的钱设置为x 则为:
a0 = x*( 2^n - 1/ 2^n ) // a0为初始有多少铜板,x为每次付的钱, n为多少次以后用光所有钱
具体写成代码如下:
int f(int n, int x)
{
return x*((pow(2,n) - 1)/pow(2,n));
}
int main()
{
int x = 0;
int count_max = 5;
int money = 32;
x = f(count_max, money);
cout << "原来有 " << x << " 个铜板" << endl;
system("pause"):
return 0;
}
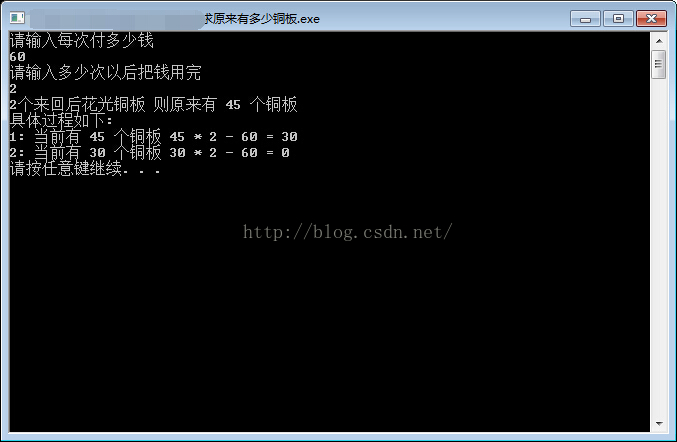
运行结果如下: