案例1——一维搜索方法
函数为:
,
log为自然对数。
- 利用MATLAB绘制函数在区间[1,2]上的变化曲线,验证在该区间上是单峰的。
- 利用黄金分割法把区间压缩到长度只有0.23,给出所有中间结果。
- 使用斐波那契法实现,其中 ,列出中间结果。
画函数图像f.m:
% f.m
function y=f(x)
y=8*exp(1-x)+7*log(x);
%{
运行-画图
fplot('f',[1 2]);
xlabel('x');
ylabel('f(x)');
%}

利用黄金分割法实现:
%Matlab routine for Golden Section Search
left=1;
right=2;
uncert=0.23;%最终的压缩长度
rho=(3-sqrt(5))/2;
N=ceil(log(uncert/(right-left))/log(1-rho)) %print N
lower='a';
a=left+(1-rho)*(right-left);
f_a=f(a);
for i=1:N,
if lower=='a'
b=a
f_b=f_a
a=left+rho*(right-left)
f_a=f(a)
else
a=b
f_a=f_b
b=left+(1-rho)*(right-left)
f_b=f(b)
end %if
if f_a<f_b
right=b;
lower='a'
else
left=a;
lower='b'
end %if
New_Interval = [left,right]
end %for i
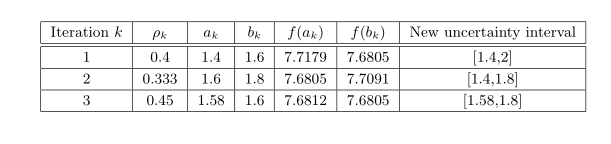
黄金分割法中间结果为:

利用斐波那契数列法实现:
%Matlab routine for Fibonacci Search technique
left=1;
right=2;
uncert=0.23;
epsilon=0.05;
F(1)=1;
F(2)=1;
N=0;
while F(N+2) < (1+2*epsilon)*(right-left)/uncert
F(N+3)=F(N+2)+F(N+1);
N=N+1;
end %while
N %print N
lower='a';
a=left+(F(N+1)/F(N+2))*(right-left);
f_a=f(a);
for i=1:N,
if i~=N
rho=1-F(N+2-i)/F(N+3-i)
else
rho=0.5-epsilon
end %if
if lower=='a'
b=a
f_b=f_a
a=left+rho*(right-left)
f_a=f(a)
else
a=b
f_a=f_b
b=left+(1-rho)*(right-left)
f_b=f(b)
end %if
if f_a<f_b
right=b;
lower='a'
else
left=a;
lower='b'
end %if
New_Interval = [left,right]
end %for i
斐波那契数列法中间结果:
案例2——多维搜索方法中的一维搜索方法
利用最速下降法求解下个函数极小值:
y=[4*(x(1)-4).^3; 2*(x(2)-3); 16*(x(3)+5).^3];
停止规则为 。初始点为[-4,5,1]
1.函数设置(g.m)
function y=g(x)
y=[4*(x(1)-4).^3; 2*(x(2)-3); 16*(x(3)+5).^3];
2.一维搜索方法设置(linesearch_secant.m)
function alpha=linesearch_secant(grad,x,d)
%Line search using secant method
%{
grad为函数
x为初始点
d为方向搜索方向
使得目标函数到达极小点为一维搜索的目标
alpha为一维搜索参数和返回值(类似于迭代x,这里迭代alpha)
%}
epsilon=10^(-4); %line search tolerance
max = 100; %maximum number of iterations
alpha_curr=0;%当前alpha值
alpha=0.001; %下一个alpha值
dphi_zero=feval(grad,x)'*d; % 初始函数值的导数与搜索方向的乘积
dphi_curr=dphi_zero;
i=0;
while abs(dphi_curr)>epsilon*abs(dphi_zero),
%alpha值设置
alpha_old=alpha_curr;
alpha_curr=alpha;
%函数值设置
dphi_old=dphi_curr;
dphi_curr=feval(grad,x+alpha_curr*d)'*d;
%割线法
alpha=(dphi_curr*alpha_old-dphi_old*alpha_curr)/(dphi_curr-dphi_old);
%终止条件判断
i=i+1;
if (i >= max) & (abs(dphi_curr)>epsilon*abs(dphi_zero)),
disp('Line search terminating with number of iterations:');
disp(i);
break;
end
end %while
3.最速梯度下降法
这个案例采用最速下降法来作为多维搜索算法,最速下降法为梯度下降法的一种具体实现,它的基本理念为:为每次迭代选择合适的步长使得目标函数能够最大程度的减到最小。它的运行方式为:从迭代点出发,沿着负梯度方向开展一维搜索,直到找到步长的最优值,则确定新的迭代点。一个最速下降法的运行方式示例如下图:

再来回顾一下多维搜索方法中的一维搜索方法:

可以看出,当前的迭代点和搜索方向确定之后,迭代点只能想确定方向移动(红色框内的直线),此时一维搜索方法就是找到移动方向上对应多维目标函数(红色框内的红色曲线)的最小值。
function [x,N]=steep_desc(grad,xnew,options);
%{
运行程序
options(2) = 10^(-6);
options(3) = 10^(-6);
steep_desc('g',[-4;5;1],options)
%}
if nargin ~= 3
options = [];
if nargin ~= 2
disp('Wrong number of arguments.');
return;
end
end
if length(options) >= 14
if options(14)==0
options(14)=1000*length(xnew);
end
else
options(14)=1000*length(xnew);
end
clc;
format compact;
format short e;
options = foptions(options);
print = options(1);
epsilon_x = options(2);
epsilon_g = options(3);
max_iter=options(14);
for k = 1:max_iter,
xcurr=xnew;
g_curr=feval(grad,xcurr);
if norm(g_curr) <= epsilon_g
disp('Terminating: Norm of gradient less than');
disp(epsilon_g);
k=k-1;
break;
end %if
alpha=linesearch_secant(grad,xcurr,-g_curr);
xnew = xcurr-alpha*g_curr;
if print,
disp('Iteration number k =')
disp(k); %print iteration index k
disp('alpha =');
disp(alpha); %print alpha
disp('Gradient = ');
disp(g_curr'); %print gradient
disp('New point =');
disp(xnew'); %print new point
end %if
if norm(xnew-xcurr) <= epsilon_x*norm(xcurr)
disp('Terminating: Norm of difference between iterates less than');
disp(epsilon_x);
break;
end %if
if k == max_iter
disp('Terminating with maximum number of iterations');
end %if
end %for
if nargout >= 1
x=xnew;
if nargout == 2
N=k;
end
else
disp('Final point =');
disp(xnew');
disp('Number of iterations =');
disp(k);
end %if
在命令行使用如下语句运行程序:
options(2) = 10^(-6);
options(3) = 10^(-6);
steep_desc('g',[-4;5;1],options)
最终结果为:


