题目地址
<前言>
高手训练矩乘第三题。
有幸分锅,无能无力。
望谅解。
<正文>
题目大意
给你一个k维每维长n的斐波那契数维体。
求值的和。
eg:以下为2维长4的表。
| (1) | (2) | (3) | (4) |
|---|---|---|---|
| 1 | 1 | 2 | 3 |
| 1 | 2 | 3 | 5 |
| 2 | 3 | 5 | 8 |
| 3 | 5 | 8 | 13 |
求和即可,题意简单易懂。
\(n,k\leq5\)
直接列出n维表,暴力统计。
预计得分20
(无脑向)
\(k=1\)
一维数表?好办。
斐波那契前缀和公式:
\[ f_1+f_2+……+f_i=f_{i+2}-1 \]
暴力矩乘n+2项,再减一。
基本的斐波那契转移大概可以直接套模板。
预计得分20.
部分分向。
\(k\leq100\)
可能就是不用矩阵快速幂的得分吧,不懂就瞎猜的zqy。
总之我也没写,有兴趣自己写吧。
直接递推的话大概可能似乎就是这个分,我已经懒得思考了。
讲一下递推的思路:
- 设\(S(k,i)\)为第i层k-1维超立方体的总和。这么说十分抽象,关键是高手训练的题解上写的东西不是人能看的,花了我好久时间理解。
举个栗子:
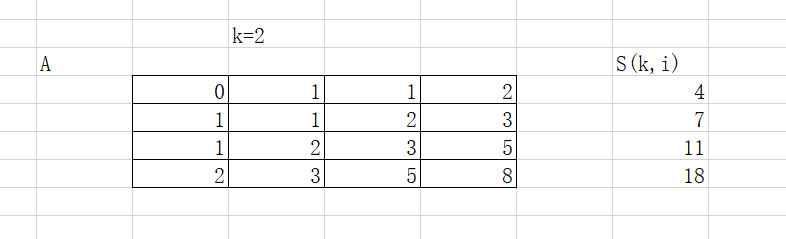
高维的以此类推,相当于将k-1维超立方体看成一大块,k维超立方体中总共有n大块,S就是其中第i大块的价值和。
- 理解这个后。我们发现答案为\(S(k+1,1)\),k-1与k之间的转移:\[\begin{aligned}&S(k,0)=\sum _{i=0}^{i<n} S(k-1,i)\\& S(k,1)=\sum_{i=1}^{i\leq n}S(k-1,i)\\&S(k,i)=S(k,i-1)+S(k,i-2)[i>=2]\end{aligned}\]
初值:这个。。。显然啊,等价形式的两种表达而已。
递推:找规律易得\cy,别管怎么来的,反正它就是个类斐波那契数列。
然后答案你就可以暴力计算了。预计得分就是这个部分分吧。(瞎猜无证)
\(T \leq 100,n,k \leq 10^9\)
看到这个数据范围,少年你们还在等什么,log级算法没跑了啊,矩乘走起。
然后你发现事情十分棘手,对于给定的k,怎么快速计算\(\sum _{i=1}^{i \leq n}S(k,i)\)呢?
因为每个k的数列都是类f数列,\(S(k,i)\)可以用\(aS(k,0)+bS(k,1)\)表示,a,b为斐波那契数列相邻两项,后边的事大概就是求一个ab的前缀和,瞎搞就成。
矩乘的具体步骤,可以参考
\[ \begin{bmatrix}F_{i-1}&F_i\end{bmatrix}=\begin{bmatrix}F_{i-2}&F_{i-1}\end{bmatrix} \begin{bmatrix} 0 &1\\1&1\end{bmatrix}\\ \begin{bmatrix}S(k,0)&S(k,1)\end{bmatrix}=\begin{bmatrix}S(k-1,0)&S(k-1,1)\end{bmatrix}\begin{bmatrix}F_n&F_{n+1}-1\\F_{n+1}-1&F_{n+1}-1\end{bmatrix} \]
至于上面的转移矩阵,其实是可以根据斐波那契前缀和公式推导得到的。
然后就两个矩乘,完结撒花。
\(\mathrm{Code:}\)
#include <bits/stdc++.h>
#define mod 1000000007
#define int long long
using namespace std;
int read()
{
int s = 0, w = 1;
char c = getchar();
while ((c < '0' || c > '9') && c != '-') c = getchar();
if (c == '-')
w = -1, c = getchar();
while (c <= '9' && c >= '0') s = (s << 3) + (s << 1) + c - '0', c = getchar();
return s * w;
}
inline int mul(int a, int b) { return 1LL * a * b % mod; }
inline int add(int a, int b) { return a + b >= mod ? a + b - mod : a + b; }
struct matrix
{
int a[10][10];
int n, m;
inline matrix(int nn,int mm)
{
n = nn;
m = mm;
memset(a, 0, sizeof(a));
}
inline matrix operator*(matrix b)
{
matrix c(n,b.m);
for (int i = 0; i < c.n; ++i)
for (int j = 0; j < c.m; ++j)
for (int k = 0; k < m; ++k)
c.a[i][j] = add(c.a[i][j], mul(a[i][k], b.a[k][j]));
return c;
}
};
int n, T, k;
matrix mpower(matrix a, int b)
{
matrix s(a.n,a.n);
for (int i = 0; i < s.n; ++i) s.a[i][i] = 1;
for (; b; b >>= 1)
{
if (b & 1)
s = s * a;
a = a * a;
}
return s;
}
signed main()
{
T = read();
while (T--)
{
matrix a(1,2), d(2,2), dd(2,2), f(1,2);
a.a[0][1] = 1;
d.a[0][1] = d.a[1][0] = d.a[1][1] = 1;
n = read();
k = read();
a = a * mpower(d, n );
int a1 = a.a[0][0], b1 = a.a[0][1], a2 = a.a[0][1], b2 = a.a[0][1]+a.a[0][0];
dd.a[0][0] = a1;
dd.a[0][1] = a2 - 1;
dd.a[1][0] = b1 - 1;
dd.a[1][1] = b2 - 1;
f.a[0][1] = 1;
f = f * mpower(dd, k);
printf("%lld\n", f.a[0][1]);
}
return 0;
}瞎写的程序,不能信。
——来自菜鸡zqy的祝福。
寒假要结束了,容我缓缓。
这题,说实话,我是30号晚上爆肝搞得。
在此之前这题没搞过。唉