1.概要:本文以 x(n)=sin(2*π*f1*n+π/3)+10*\sin(6*π*f2*n+π/4)+wgn(0,sigma)
为例进行其功率谱的估计及观察sigma参数对f1,f2估计的影响,影响情况以MSE为衡量标准
(注:f1规定为0.1,f2规定为0.3。n的取值为[1,256],wgn(0,sigma)是0均值,标准差为sigma的高斯分布的随机数)
2.随机信号功率谱的估计方法:对于平稳随机信号,其功率谱与其自相关函数为傅里叶变换对。对于本例而言,其均值E[x(n)]为0,自相关函数R(m)与时间起点无关,只与时间间隔m有关因而具有平稳性,可以直接运用维纳-欣钦定理。如果是不具有平稳性的话可以把其自相关函数取均值得到E[R]再运用维纳欣钦定理。
3.自相关的估计方法:通过上文内容可以知道,对于随机信号来说,其自相关函数是得到功率谱的重要途径。常用的自相关估计方法有两种:
-
(1)
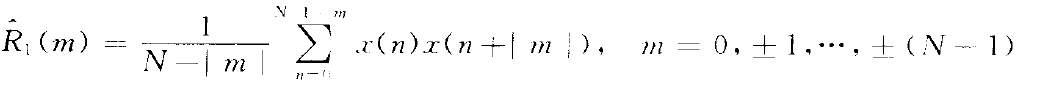
这种估计方法的均值为:
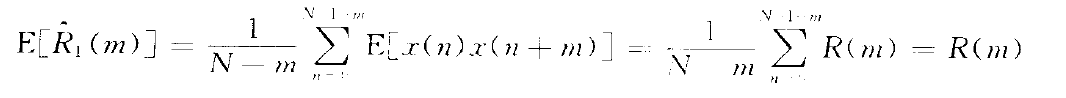
方差为:
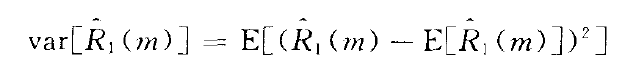
可以看到这种估计方法是一种无偏估计 -
(2.)
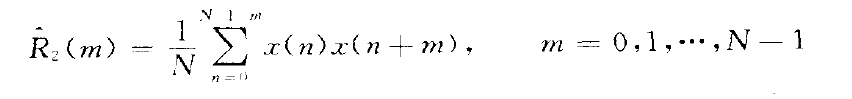
均值为:

当N趋近于无穷时是无偏估计。 -
两种估计的性能比较:
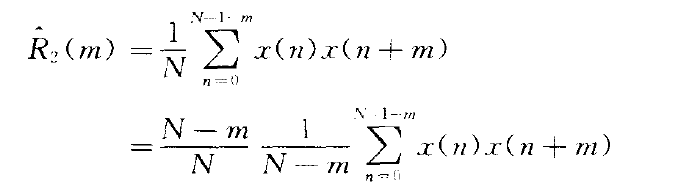
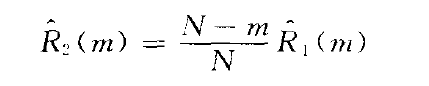

一般用第二种方法去估计自相关。

4.估计参数f1和f2的方法:本例是一个实函数,其功率谱是有偶对称形状的。故其谱上一定会出现一高一低两个峰,两个峰出现的位置理论来说是在DTFT频谱的0.2π和0.6π处。但计算机无法处理DTFT,只能处理DFT和FFT。DTF是对DTFT在[0,2π]内的等间隔采样,FFT则是DFT的快速运算版本。在DFT的频谱横坐标是采样点的序号,我们需要由这样一个序号去转换到频率。这里我使用的方法就是在一定的范围内把寻找两个最大峰的横坐标,以256点DFT为例,那么横坐标的值乘以1/256得到就是f1和f2的估计值。
5.参数估计好坏的衡量指标:MSE均方误差

6.程序实现:功率谱估计
#随机信号功率谱估计
import numpy as np
import matplotlib.pyplot as plt
from math import *
#n取值从1到256
def signal(n):
if(n<1 or n>256):
return 0
else:
return (sin(0.2*pi*n+pi/3)+10*sin(0.6*pi*n+pi/4)+np.random.normal(0,1,1)[0])
#生成WN项(旋转因子)
def wn_k(k,n,N):
return complex(cos(2*pi*n*k/N),sin(-2*pi*n*k/N))
#自相关估计:
f1_true=0.1
f2_true=0.3
R=[]#存放自相关函数序列
power_spectrum=[]
sums=0
N=256
#估计自相关
for m in range(0,256):
for n in range (1,257-m):
sums=sums+(signal(n)*signal(n+m)/N)
R.append(sums)
sums=0
#对自相关求DFT得到功率谱
for k in range(0,N):
for n in range(0,N):
#n的取值为从0到255
sums=sums+R[n]*wn_k(k,n,N)
power_spectrum.append(sums)
sums=0
f1=(np.argmax(power_spectrum[10:50])+10)/256
f2=(np.argmax(power_spectrum[50:100])+50)/256
print("f1:%f,f2:%f"%(f1,f2))
x=np.linspace(0,255,256)
plt.stem(x,np.abs(power_spectrum))
plt.suptitle("estimate f1:%f,estimate f2:%f"%(f1,f2))
plt.show()
结果如下:

在程序里:
f1=(np.argmax(power_spectrum[10:50])+10)/256
f2=(np.argmax(power_spectrum[50:100])+50)/256
print(“f1:%f,f2:%f”%(f1,f2))
x=np.linspace(0,255,256)
plt.stem(x,np.abs(power_spectrum))
plt.suptitle(“estimate f1:%f,estimate f2:%f”%(f1,f2))
plt.show()
这段代码就是由估计出来的功率谱去计算f1和f2并将其显示出来。与理论值0.1,0.3比较接近
7.程序实现,高斯分布方差对f1与f2估计值的影响(影响大小用MSE来衡量)
import numpy as np
import matplotlib.pyplot as plt
from math import *
def signal(n,sigma):
if(n<1 or n>256):
return 0
else:
return (2*sin(0.2*pi*n+pi/3)+10*sin(0.6*pi*n+pi/4)+np.random.normal(0,sigma,1)[0])
def estimate(sigma):
R=[]#存放自相关函数序列
power_spectrum=[]
sums=0
N=256
#计算自相关
for m in range(0,256):
for n in range (1,257-m):
sums=sums+(signal(n,sigma)*signal(n+m,sigma)/N)
R.append(sums)
sums=0
#对自相关求FFT得到功率谱
trans=np.fft.fft(R,n=256)
for x in range(0,256):
power_spectrum.append(trans[x]**2)
f1=(np.argmax(power_spectrum[10:50])+10)/256
f2=(np.argmax(power_spectrum[50:100])+50)/256
return [f1,f2]
sum_f1=0
sum_f2=0
MSE_f1=[]
MSE_f2=[]
counter=20
#外层循环控制方差
#内层循环控制参与平均的次数
for x in range(16,0,-2):
#暂存每次得到的f1,f2
f1=[]
f2=[]
for y in range(0,counter):
temp1,temp2=estimate(x)
f1.append(temp1)
f2.append(temp2)
sum_f1=sum_f1+temp1
sum_f2=sum_f2+temp2
mean_f1=sum_f1/counter
mean_f2=sum_f2/counter
bia_f1=0.1-mean_f1
bia_f2=0.3-mean_f2
for z in range(0,counter):
f1[z]=(f1[z]-mean_f1)**2
f2[z]=(f2[z]-mean_f2)**2
var_f1=sum(f1)/counter
var_f2=sum(f2)/counter
MSE_f1.append(var_f1+bia_f1**2)
MSE_f2.append(var_f2+bia_f2**2)
sum_f1=0
sum_f2=0
plt.subplot(2,1,1)
plt.plot(MSE_f1)
plt.title("MSE f1~SNR")
plt.subplot(2,1,2)
plt.plot(MSE_f2)
plt.title("MSE f2~SNR")
plt.show()
程序运行的结果每次都不同,这种仿真称为蒙特卡洛仿真。我们可以看到,在方差还不是太大时对于f2的估计影响不大,但对于f1的影响较大。我们取20次估计的总和取平均作为在某一方差下的估计值,通过外层循环控制方差逐渐减小来观察估计的性能指标


可以看到程序运行的结果不是一样的,f1的MSE曲线也不是理论上的完美的单调递减曲线。但整体趋势还是随着噪声方差减小估计值的性能随之提高。两图中f2基本是0,f1则之间趋近于一致估计。
当噪声方差很大时:例如标准差取为100



可以看到,在参数完全不变的情况下运行三次结果变化比较大,从图中的标题可以看到f2的估值也开始变得不准确。如果把噪声均值也提高的话会更不准确。当噪声很大时,已经把原信号给淹没了,估计自然就不准确了
