目录
本系列是这本算法教材的扩展资料:《算法竞赛入门到进阶》(京东 当当 ) 清华大学出版社
PDF下载地址:https://github.com/luoyongjun999/code 其中的“补充资料”
如有建议,请联系:(1)QQ 群,567554289;(2)作者QQ,15512356
@
《算法竞赛入门到进阶》的第4章“搜索技术”,讲解了递归、BFS、DFS的原理,以及双向广搜、A*算法、剪枝、迭代加深搜索、IDA*的经典例题,适合入门搜索算法。
本文分几篇专题介绍搜索扩展内容、讲解更多习题,便于读者深入掌握搜索技术。
第1篇:搜索基础。
第2篇:剪枝。
第3篇:广搜进阶。
第4篇:迭代加深、A*、IDA*。
本文是第3篇。
本篇深入地讲解了双向广搜、BFS+优先队列、BFS+双端队列的算法思想和应用,帮助读者对BFS的理解更上一层楼。
1 双向广搜
1.1 双向广搜的原理和复杂度分析
双向广搜的应用场合:有确定的起点和终点,并且能把从起点到终点的单个搜索,变换为分别从起点出发和从终点出发的“相遇”问题,可以用双向广搜。
从起点s(正向搜索)和终点t(逆向搜索)同时开始搜索,当两个搜索产生的一个子状态v相同时就结束。得到的s-v-t是一条最佳路径,当然,最佳路径可能不止这一条。
注意,和普通BFS一样,双向广搜在搜索时并没有“方向感”,所谓“正向搜索”和“逆向搜索”其实是盲目的,它们从s和t逐层扩散出去,直到相遇为止。
与只做一次BFS相比,双向BFS能在多大程度上改善算法复杂度?下面以网格图和树形结构为例,推出一般性结论。
(1)网格图。
用BFS求下面图中两个黑点s和t间的最短路。左图是一个BFS;右图是双向BFS,在中间的五角星位置相遇。

设两点的距离是k。左边的BFS,从起点s扩展到t,一共访问了\(2k(k+1)≈2k^2\)个结点;右边的双向BFS,相遇时一共访问了约\(k^2\)个结点。两者差2倍,改善并不明显。
在这个网格图中,BFS扩展的第k和第k+1层,结点数量相差(k+1)/k倍,即结点数量是线性增长的。
(2)树形结构。
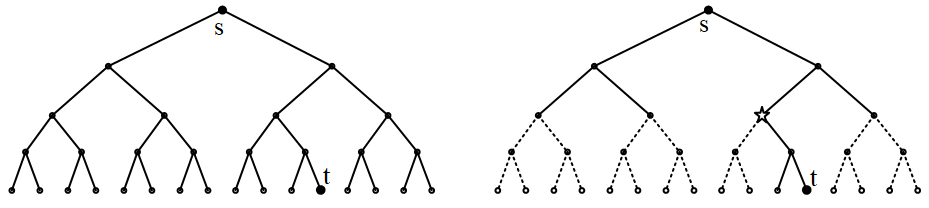
以二叉树为例,求根结点s到最后一行的黑点t的最短路。
左图做一次BFS,从第1层到第k层,共访问\(1 + 2 +...+ 2^{k-1} ≈ 2^k\)个结点。右图是双向BFS,分别从上往下和从下往上BFS,在五角星位置相遇,共访问约\(2×2^{k/2}\)个结点。双向广搜比做一次BFS改善了\(2^{k/2}\)倍,优势巨大。
在二叉树的例子中,BFS扩展的第k和第k+1层,结点数量相差2倍,即结点数量是指数增长的。
从上面2个例子可以得到一般性结论:
(1)做BFS扩展的时候,下一层结点(一个结点表示一个状态)数量增加越快,双向广搜越有效率。
(2)是否用双向广搜替代普通BFS,除了(1)以外,还应根据总状态数量的规模来决定。双向BFS的优势,从根本上说,是它能减少需要搜索的状态数量。有时虽然下一层数量是指数增长的,但是由于去重或者限制条件,总状态数并不多,也就没有必要使用双向BFS。例如后面的例题“hdu 1195 open the lock”,密码范围1111~9999,共约9000种,用BFS搜索时,最多有9000个状态进入队列,就没有必要使用双向BFS。而例题HDU 1401 Solitaire,可能的棋局状态有1500万种,走8步棋会扩展出168种状态,大于1500万,相当于扩展到所有可能的棋局,此时应该使用双向BFS。
很多教材和网文讲解双向广搜时,常用八数码问题做例子。下图引用自《算法竞赛入门到进阶》4.3.2节,演示了从状态A移动到状态F的搜索过程。
八数码共有9! = 362880种状态,不太多,用普通BFS也行。不过,用双向广搜更好,因为八数码每次扩展,下一层的状态数量是上一层的2~4倍,比二叉树的增长还快,效率的提升也就更高。

1.2 双向广搜的实现
双向广搜的队列,有两种实现方法:
(1)合用一个队列。正向BFS和逆向BFS用同一个队列,适合正反2个BFS平衡的情况。正向搜索和逆向搜索交替进行,两个方向的搜索交替扩展子状态,先后入队。直到两个方向的搜索产生相同的子状态,即相遇了,结束。这种方法适合正反方向扩展的新结点数量差不多的情况,例如上面的八数码问题。
(2)分成两个队列。正向BFS和逆向BFS的队列分开,适合正反2个BFS不平衡的情况。让子状态少的BFS先扩展下一层,另一个子状态多的BFS后扩展,可以减少搜索的总状态数,尽快相遇。例题见后面的“洛谷p1032 字串变换”。
和普通BFS一样,双向广搜在扩展队列时也需要处理去重问题。把状态入队列的时候,先判断这个状态是否曾经入队,如果重复了,就丢弃。
1.3 双向广搜例题
1.hdu 1195 open the lock
http://acm.hdu.edu.cn/showproblem.php?pid=1195
题目描述:打开密码锁。密码由四位数字组成,数字从1到9。可以在任何数字上加上1或减去1,当'9'加1时,数字变为'1',而'1'减1时,数字变为'9'。相邻的数字可以交换。每个动作是一步。任务是使用最少的步骤来打开锁。注意:最左边的数字不是最右边的数字的邻居。
输入:输入文件以整数T开头,表示测试用例的数量。
每个测试用例均以四位数N开头,指示密码锁定的初始状态。然后紧跟另一行带有四个下标M的行,指示可以打开锁的密码。每个测试用例后都有一个空白行。
输出:对于每个测试用例,一行中打印最少的步骤。
样例输入:
2
1234
2144
1111
9999
样例输出:
2
4
---------------------------------------------------------------------
题解:
题目中的4位数字,走一步能扩展出11种情况;如果需要走10步,就可能有1110种情况,数量非常多,看起来用双向广搜能大大提高搜索效率。不过,这一题用普通BFS也行,因为没有1110种情况,密码范围1111~9999,只有约9000种。用BFS搜索时,最多有9000个状态进入队列,没有必要使用双向广搜。
密码进入队列时,应去重,去掉重复的密码。去重用hash最方便。
读者可以用这一题练习双向广搜。
2.HDU 1401 Solitaire
经典的双向广搜例题。
http://acm.hdu.edu.cn/showproblem.php?pid=1401
题目描述:8×8的方格,放4颗棋子在初始位置,给定4个最终位置,问在8步内是否能从初始位置走到最终位置。规则:每个棋子能上下左右移动,若4个方向已经有一棋子则可以跳到下一个空白位置。例如,图中(4,4)位置的棋子有4种移动方法。
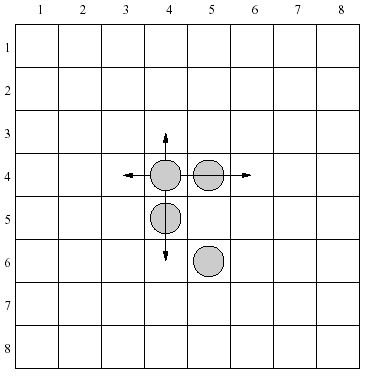
题解:
在8×8的方格上放4颗棋子,有64×63×62×61≈1500万种布局。走一步棋,4颗棋子共有16种走法,连续走8步棋,会扩展出\(16^8\)种棋局,\(16^8\)大于1500万,走8步可能会遍历到1500万棋局。
此题应该使用双向BFS。从起点棋局走4步,从终点棋局走4步,如果能相遇就有一个解,共扩展出\(2×16^4=131072\)种棋局,远远小于1500万。
本题也需要处理去重问题,扩展下一个新棋局时,看它是否在队列中处理过。用hash的方法,定义char vis[8][8][8][8][8][8][8][8]表示棋局,其中包含4个棋子的坐标。当vis=1时表示正向搜过这个棋局,vis=2表示逆向搜过。例如4个棋子的坐标是(a.x, a.y)、(b.x, b.y)、(c.x, c.y)、(d.x, d.y),那么:
vis[a.x][a.y][b.x][b.y][c.x][c.y][d.x][d.y] = 1
表示这个棋局被正向搜过。
4个棋子需要先排序,然后再用vis记录。如果不排序,一个棋局就会有很多种表示,不方便判重。
char vis[8][8][8][8][8][8][8][8] 用了\(8^8\) = 16M空间。如果定义为int,占用64M空间,超过题目的限制。
3.HDU 3095 Eleven puzzle
http://acm.hdu.edu.cn/showproblem.php?pid=3095
题目描述:如图是13个格子的拼图,数字格可以移动到黑色格子。左图是开始局面,右图是终点局面。一次移动一个数字格,问最少移动几次可以完成。
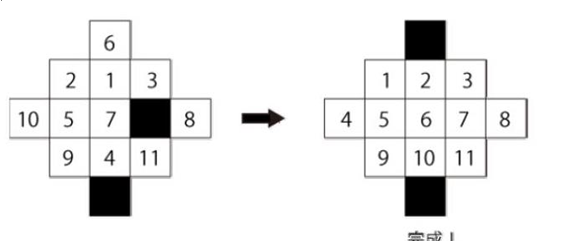
题解:
(1)可能的局面有13!,极大。
(2)用一个BFS,复杂度过高。每次移动1个黑格,移动方法最少1种,最多8种。如果移动10次,那么最多有\(8^{10}\) ≈ 10亿种。
(3)用双向广搜,能减少到\(2×8^5\) = 65536种局面。
(4)判重:可以用hash,或者用STL的map。
4.洛谷p1032 字串变换
https://www.luogu.com.cn/problem/P1032
题目描述:已知有两个字串A,B及一组字串变换的规则(至多6个规则):
A1->B1
A2->B2
规则的含义为:在A中的子串 A1可以变换为B1,A2可以变换为 B2…。
例如:A=abcd,B=xyz,
变换规则为:
abc→xu,ud→y,y→yz
则此时,A可以经过一系列的变换变为B,其变换的过程为:
abcd→xud→xy→xyz。
共进行了3次变换,使得A变换为B。
输入输出:给定字串A、B和变换规则,问能否在10步内将A变换为B,输出最少的变换步数。字符串长度的上限为20。
---------------------------------------------------------------------
题解:
(1)若用一个BFS,每层扩展6个规则,经过10步,共\(6^{10}\) ≈ 6千万次变换。
(2)用双向BFS,可以用\(2×6^5\) = 15552次变换搜完10步。
(3)用两个队列分别处理正向BFS和逆向BFS。由于起点和终点的串不同,它们扩展的下一层数量也不同,也就是进入2个队列的串的数量不同,先处理较小的队列,可以加快搜索速度。2个队列见下面的代码示例[完整代码参考:https://blog.csdn.net/qq_45772483/article/details/104504951]。
void bfs(string A, string B){ //起点是A,终点是B
queue <string> qa, qb; //定义2个队列
qa.push(A); //正向队列
qb.push(B); //逆向队列
while(qa.size() && qb.size()){
if (qa.size() < qb.size()) //如果正向BFS队列小,先扩展它
extend(qa, ...); //扩展时,判断是否相遇
else //否则扩展逆向BFS
extend(qb, ...); //扩展时,判断是否相遇
}
}5.poj 3131 Cubic Eight-Puzzle
http://poj.org/problem?id=3131
立体八数码问题。状态多、代码长,是一道难题。
2 BFS + 优先队列
2.1 优先队列
普通队列中的元素是按先后顺序进出队列的,先进先出。在优先队列中,元素被赋予了优先级,每次弹出队列的,是具有最高优先级的元素。优先级根据需求来定义,例如定义最小值为最高优先级。
优先队列有多种实现方法。最简单的是暴力法,在n个数中扫描最小值,复杂度是O(n)。暴力法不能体现优先队列的优势,真正的优先队列一般用堆这种数据结构实现[堆的概念和代码实现,见https://www.cnblogs.com/luoyj/p/12409990.html],插入元素和弹出最高优先级元素,复杂度都是O(logn)。
[^2]: 堆的概念和代码实现,见https://www.cnblogs.com/luoyj/p/12409990.html
虽然基于堆的优先队列很容易手写,不过竞赛中一般不用自己写,而是直接用STL的priority_queue。
2.2 最短路问题
BFS 结合优先队列,可解决最短路径问题。
1.算法描述
下面描述“BFS+优先队列”求最短距离的算法步骤。以下图为例,起点是A,求A到其它结点的最短路。图的结点总数是V,边的总数是E。
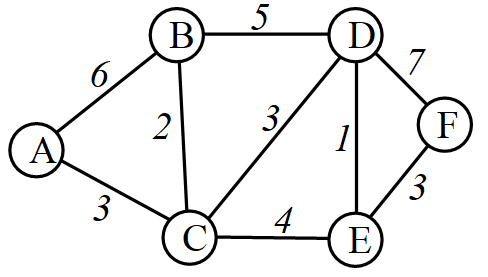
算法步骤是:
(1)扩展A的邻居结点,放到优先队列Q里:{\(B_6, C_3\)}。下标表示从A出发到这个点的路径长度。一条路径上包含了多个结点。Q中记录的是各结点到起点A的路径长度,其中有一个最短,优先队列Q可以快速取出它。
(2)从优先队列Q中弹出距离起点A最短的结点,这次是C,再把C的新邻居D、E放到Q里,并更新Q里每个点的路径长度:{\(B_5, D_6, E_7\)}。\(B_6\)更新为\(B_5\)是因为现在A可以经过C到B,总距离是5。在这一步,找到了A到C的最短路径长度,C是第一个被确定最短路径的结点。
(3)继续从优先队列Q中取出距离最短的结点,这次是B,B没有新邻居放进Q,Q现在是{\(D_6,E_7\)}。更新Q里每个点的路径长度,但这次没有更新。在这一步,找到了A到B的最短路径长度,路径是A-C-B。
继续以上过程,每个结点都会进入Q并弹出,最后Q为空时结束。
在优先队列Q里找最小值,也就是找距离最短的结点,复杂度是\(O(logV)\)。“BFS+优先队列”求最短路径,算法的总复杂度是\(O((V+E)logV)\)。共检查V+E次,每次优先队列是\(O(logV)\)。
如果不用优先队列,直接在V个点中找最小值,是O(V)的,总复杂度\(O(V^2)\)。
\(O(V^2)\)是否一定比\(O((V+E)logV)\)好?下面将讨论这个问题。
(1)稀疏图中,点和边的数量差不多,V ≈ E,用优先队列的复杂度\(O((V+E)logV)\)可以写成\(O(VlogV)\),它比\(O(V^2)\)好,是非常好的优化。
(2)稠密图中,点少于边,\(V < E\)且\(V^2 ≈ E\),复杂度\(O((V+E)logV)\)可以写成\(O(V^2logV)\),它比\(O(V^2)\)差。这种情况下,用优先队列,反而不如直接用暴力搜。
2. BFS与Dijkstra
读者如果学过最短路径算法Dijkstra[参考《算法竞赛入门到进阶》10.9.4 Dijkstra,详细地解释了Dijkstra算法,给出了模板代码],就会发现,实际上这就是用优先队列实现的Dijkstra,即:“Dijkstra + 优先队列 = BFS + 优先队列”。
根据前面的讨论,Dijkstra 算法也有下面的结论:
(1)稀疏图,用“Dijkstra + 优先队列”,复杂度\(O((V+E)logV) = O(VlogV)\);
(2)稠密图,如果\(V^2 ≈ E\),不用优先队列,直接在所有结点中找距离最短的那个点,总复杂度\(O(V^2)\)。
稀疏图的存储用邻接表或链式前向星,稠密图用邻接矩阵。
2.3 例题
下面几个题目都是“BFS+优先队列”求最短路。
1. hdu 3152 Obstacle Course
http://acm.hdu.edu.cn/showproblem.php?pid=3152
题目描述:一个N*N的矩阵,每个结点上有一个费用。从起点[0][0]出发到终点[N-1][N-1],求最短的路径,即经过的结点的费用和最小。每次移动,可以沿上下左右四个方向走一步。
输入:第一行是N,后面跟着N行,每一行有N个数字。最后一行是0,表示终止。2<=N<=125。
输出:最小费用。
输入样例:
3
5 5 4
3 9 1
3 2 7
5
3 7 2 0 1
2 8 0 9 1
1 2 1 8 1
9 8 9 2 0
3 6 5 1 5
0
输出样例:
Problem 1: 20
Problem 2: 19
---------------------------------------------------------------------
题解:
最短路径问题[题目一般不会要求打印路径,因为可能有多条最短路径,不方便系统测试。如果需要打印出最短路径,参考《算法竞赛入门到进阶》“10.9 最短路”,给出了路径打印的代码]。N很小,用矩阵存图。
下面是代码。
#include<bits/stdc++.h>
using namespace std;
const int maxn=150, INF=1<<30;
int dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
int n, graph[maxn][maxn], vis[maxn][maxn]; //vis记录到起点的最短距离
struct node{
int x,y,sum;
friend bool operator <(node a,node b) {
return a.sum > b.sum;
}
};
int bfs(){ //dijkstra
fill(&vis[0][0], &vis[maxn][0], INF);
vis[0][0] = graph[0][0]; //起点到自己的距离
priority_queue <node> q;
node first = {0, 0, graph[0][0]};
q.push(first); //起点进队
while(q.size()) {
node now = q.top(); q.pop(); //每次弹出已经找到最短距离的结点
if(now.x==n-1 && now.y==n-1) //终点:右下角
return now.sum; //返回
for(int i=0; i<4; i++){ //上下左右
node t = now; //扩展now的邻居
t.x += dir[i][0];
t.y += dir[i][1];
if(0<=t.x && t.x<n && 0<=t.y && t.y<n) { //在图内
t.sum += graph[t.x][t.y];
if(vis[t.x][t.y] <= t.sum) continue;
//邻居已经被搜过,并且距离更短,不用更新
if(vis[t.x][t.y] == INF) q.push(t); //如果没进过队列,就进队
vis[t.x][t.y] = t.sum; //更新这个结点到起点的距离
}
}
}
return -1;
}
int main(){
int k = 1;
while(cin>>n, n){
for(int i=0; i<n; i++)
for(int j=0; j<n; j++)
cin >> graph[i][j];
cout<<"Problem "<< k++ <<": "<< bfs() << endl;
}
return 0;
}2. 其他例题
类似的题目,练习:poj 1724、poj 1729、hdu 1026。
3 BFS + 双端队列
在“简单数据结构”这一节中,讲解了“双端队列和单调队列”。双端队列是一种具有队列和栈性质的数据结构,它能而且只能在两端进行插入和删除。双端队列的经典应用是实现单调队列。下面讲解双端队列在BFS中的应用。
“BFS + 双端队列”可以解决一种特殊图的最短路问题:图的结点和结点之间的边权是0或者1。
一般求解最短路,高效的算法是Dijkstra,或者“BFS+优先队列”,复杂度O((V+E)logV),V是结点数,E是边数。但是,在这类特殊图中,用“BFS+双端队列”可以在O(V)时间内求得最短路。
双端队列的经典应用是单调队列,“BFS+双端队列”的队列也是一个单调队列。
下面的例题,详细解释了算法。
洛谷 P4667 https://www.luogu.com.cn/problem/P4667
Switch the Lamp On
时间限制150ms;内存限制125.00MB。
题目描述:Casper正在设计电路。有一种正方形的电路元件,在它的两组相对顶点中,有一组会用导线连接起来,另一组则不会。有 N×M 个这样的元件,你想将其排列成N行,每行M 个。电源连接到板的左上角。灯连接到板的右下角。只有在电源和灯之间有一条电线连接的情况下,灯才会亮着。为了打开灯,任何数量的电路元件都可以转动90°(两个方向)。
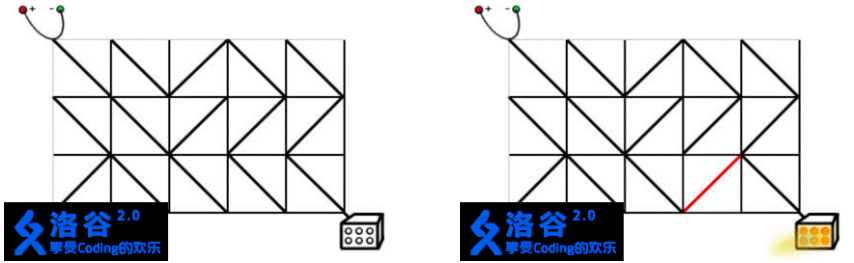
在上面的左图中,灯是关着的。在右图中,右数第二列的任何一个电路元件被旋转90°,电源和灯都会连接,灯被打开。现在请你编写一个程序,求出最小需要多少旋转多少电路元件。
输入格式:
输入的第一行包含两个整数N和M,表示盘子的尺寸。 在以下N行中,每一行有M个符号\或/,表示连接对应电路元件对角线的导线的方向。 1≤N, M≤500。
输出格式:
如果可以打开灯,那么输出一个整数,表示最少转动电路元件的数量。
如果不可能打开灯,输出"NO SOLUTION"。
样例输入:
3 5
\/\
\///
/\\
样例输出:
1
---------------------------------------------------------------------
题解:
(1)建模为最短路径问题
题目可以转换为最短路径问题。把起点s到终点t的路径长度,记录为需要转的元件数量。从一个点到邻居点,如果元件不转,距离是0,如果需要转元件,距离是1。题目要求找s到t的最短路径。样例的网络图如下图,其中实线是0,虚线是1。

(2)BFS +优先队列
用上一节的最短路径算法“BFS+优先队列”,复杂度是O((V+E)logV)。题目中结点数V = N×M = 250,000,边数E = 2×N×M = 500,000,O((V+E)logV) ≈ 1.5千万,题目给的时间限制是150ms,超时。
(3)BFS + 双端队列
如果读者透彻理解“BFS + 优先队列”的思想,就能知道优先队列的作用,是在队列中找到距离起点最短的那个结点,并弹出它。使用优先队列的原因是,每个结点到起点的距离不同,需要用优先队列来排序,找最小值。
在特殊的情况下,有没有更快的办法找到最小值?
这种特殊情况就是本题,边权是0或者1。简单地说,就是:“边权为0,插到队头;边权为1,插入队尾”,这样就省去了排序操作。
下面结束“BFS + 双端队列”计算最短路径的过程。
1)把起点s放进队列。
2)弹出队头s。扩展s的直连邻居g,边权为0的距离最短,直接插到队头;边权为1的直接插入队尾。在样例中,当前队列是:{\(g_0\)},下标记录结点到起点s的最短距离。
3)弹出队头\(g_0\),扩展它的邻居b、n、q,现在队列是:{\(q_0,b_1,n_1\)},其中的\(q_0\),因为边权为0,直接放到了队头。g被弹出,表示它到s的最短路已经找到,后面不再进队。
4)弹出\(q_0\),扩展它的邻居g、j、x、z,现在队列是{\(j_0, z_0, b_1, n_1, x_1\)},其中\(j_0\)、\(z_0\)边权为0,直接放到队头。
等等。
下面的表格给出了完整的过程。
| 步骤 | 出队 | 邻居 | 进队 | 当前队列 | 最短路 | 说明 |
|---|---|---|---|---|---|---|
| 1 | \(s\) | {\(s\)} | ||||
| 2 | \(s\) | \(g\) | \(g\) | {\(g_0\)} | \(s\)-\(s\): 0 | |
| 3 | \(g_0\) | \(s、b、n、q\) | \(b、n、q\) | {\(q_0,b_1,n_1\)} | \(s\)-\(g\): 0 | \(s\)已经进过队,不再进队 |
| 4 | \(q_0\) | \(g、j、x、z\) | \(j、x、z\) | {\(j_0,z_0,b_1,n_1,x_1\)} | \(s\)-\(q\): 0 | \(g\)不再进队 |
| 5 | \(j_0\) | \(b、d、q、u\) | \(d、u\) | {\(z_0,b_1,n_1,x_1,d_1,u_1\)} | \(s\)-\(j\): 0 | \(q、b\)已经进过队,不再进队 |
| 6 | \(z_0\) | \(q、u\) | {\(b_1,n_1,x_1,d_1,u_1\)} | \(s\)-\(z\): 0 | \(q、u\)已经进过队,不再进队 | |
| 7 | \(b_1\) | \(g、j\) | {\(n_1,x_1,d_1,u_1\)} | \(s\)-\(b\): 1 | \(g、j\)不再进队 | |
| 8 | \(n_1\) | \(g、x\) | {\(x_1,d_1,u_1\)} | \(s\)-\(n\): 1 | \(g、x\)不再进队 | |
| 9 | \(x_1\) | \(n、q\) | {\(d_1,u_1\)} | \(s\)-\(x\): 1 | \(n、q\)不再进队 | |
| 10 | \(d_1\) | \(j、m\) | \(m\) | {\(m_1,u_1\)} | \(s\)-\(d\): 1 | \(m\)放队首,但距离是1,\(s-d_1-m_0\) |
| 11 | \(m_1\) | \(d、u\) | {\(u_1\)} | \(s\)-\(m\): 1 | \(d、u\)不再进队 | |
| 12 | \(u_1\) | \(m、z、j、t\) | \(t\) | {\(t_1\)} | \(s\)-\(u\): 1 | \(m、z、j\)不再进队 |
| 13 | \(t_1\) | \(u\) | {} | \(s\)-\(t\): 1 | 队列空,停止 |
注意几个关键:
1)如果允许结点多次进队,那么先进队时算出的最短距离,大于后进队时算出的最短距离。所以后进队的结点,出队时直接丢弃。当然,最好不允许结点再次进队,在代码中加个判断即可,代码中的dis[nx][ny] > dis[u.x][u.y] + d起到了这个作用。
2)结点出队时,已经得到了它到起点s的最短路。
3)结点进队时,应该计算它到s的路径长度再入队。例如u出队,它的邻居v进队,进队时,v的距离是s-u-v,也就是u到s的最短距离加上(u,v)的边权。
为什么“BFS+双端队列”的算法过程是正确的?仔细思考可以发现,出队的结点到起点的最短距离是按0、1、2...的顺序输出的,也就是说,距离为0的结点先输出,然后是距离为1的结点.....这就是双端队列的作用,它保证距离更近的点总在队列前面,队列是单调的。
算法的复杂度,因为每个结点只入队和出队一次,所以复杂度是O(V),V是结点数量。
下面是代码[改编自:https://www.luogu.com.cn/blog/hje/solution-p4667],其中的双端队列用STL的deque实现。
#include<bits/stdc++.h>
using namespace std;
const int dir[4][2] = {{-1,-1},{-1,1},{1,-1},{1,1}}; //4个方向的位移
const int ab[4] = {2,1,1,2}; //4个元件期望的方向
const int cd[4][2] = {{-1,-1},{-1,0},{0,-1},{0,0}}; //4个元件编号的位移
int graph[505][505],dis[505][505]; //dis记录结点到起点s的最短路
struct P{
int x,y,dis;
}u;
int Get(){
char c;
while((c=getchar())!='/' && c != '\\') ; //字符不是'/'和'\'
return c=='/'?1:2;
}
int main(){
int n, m; cin >>n >>m;
memset(dis,0x3f,sizeof(dis));
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
graph[i][j] = Get();
deque <P> dq;
dq.push_back((P){1,1,0});
dis[1][1]=0;
while(!dq.empty()){
u = dq.front(), dq.pop_front(); //front()读队头,pop_front()弹出队头
int nx,ny;
for(int i=0;i<=3;++i) { //4个方向
nx = u.x+dir[i][0];
ny = u.y+dir[i][1];
int d = 0; //边权
d = graph[u.x+cd[i][0]][u.y+cd[i][1]]!=ab[i]; //若方向不相等,则d=1
if(nx && ny && nx<n+2 && ny<m+2 && dis[nx][ny]>dis[u.x][u.y]+d){
//如果一个结点再次进队,那么距离应该更小。实际上,由于再次进队时,距离肯定更大,所以这里的作用是阻止再次入队。
dis[nx][ny] = dis[u.x][u.y]+d;
if(d==0) dq.push_front((P){nx, ny, dis[nx][ny]}); //边权为0,插到队头
else dq.push_back ((P){nx, ny, dis[nx][ny]}); //边权为1,插到队尾
if(nx==n+1 && ny==m+1) //到终点退出。不退也行,队列空自动退出
break;
}
}
}
if(dis[n+1][m+1] != 0x3f3f3f3f) //可能无解,即s到t不通
cout << dis[n+1][m+1];
else
cout <<"NO SOLUTION";
return 0;
} 致谢
谢勇,湘潭大学算法竞赛教练:讨论最短路径算法的复杂度。