Educational Codeforces Round（div2）补题A B

A. K-divisible Sum

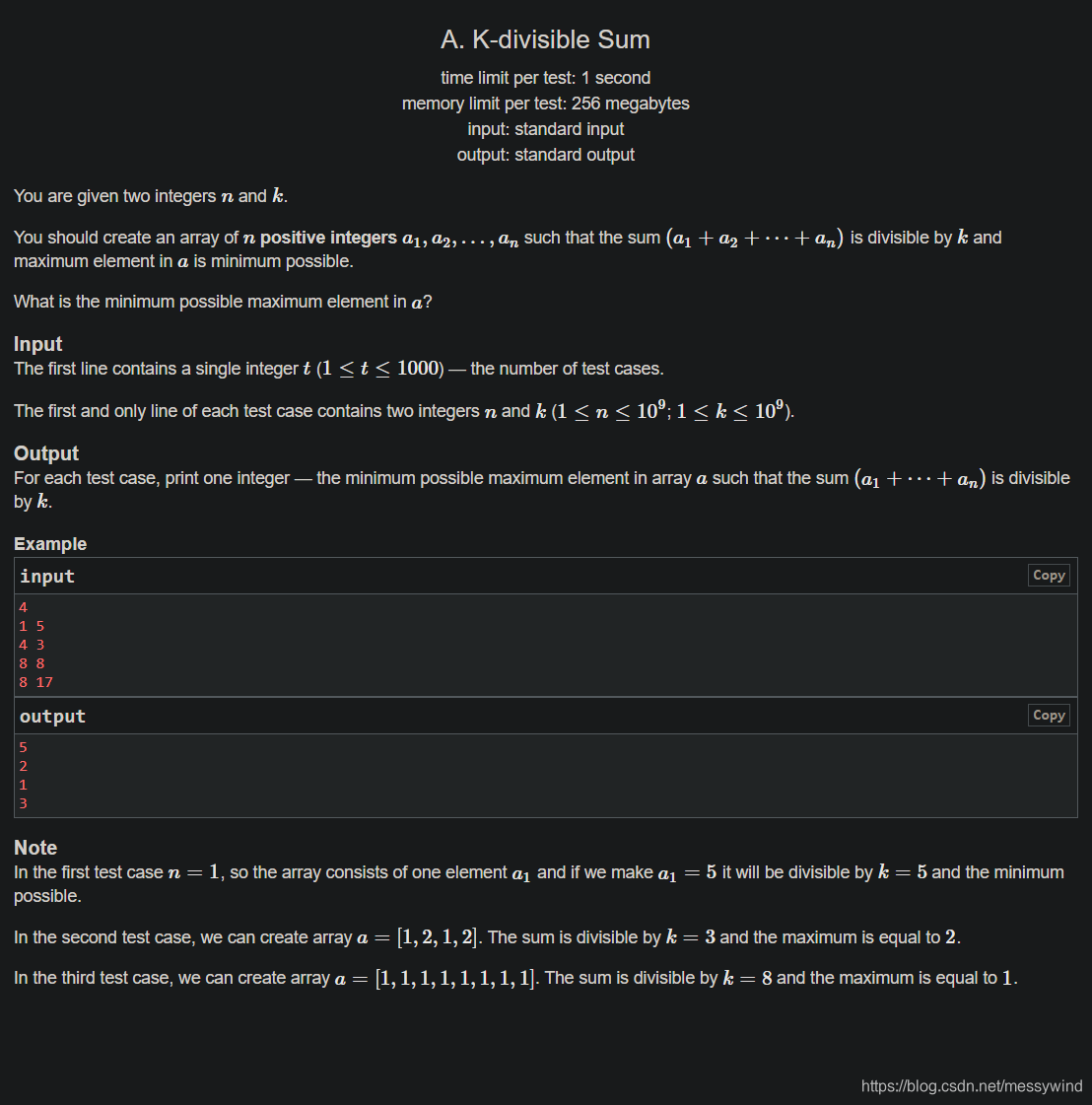
分析： 数学题。分情况讨论。
$n=k$时，必定全为$1$；
$n<k$时，如果$k$能够被$n$整除，那就输出$n/k$，否则要$+1$；
$n>k$时，如果$n$能整除$k$，那么所有数最小可以全部为$1$，如果不能整除，直接输出$2$，因为一个数本身和他两倍之间的所有数必定可以找到一个数使其整除$k$。

代码：

#include<iostream>
using namespace std;
int t;
long long int n,k;
int main(){
    
    
    scanf("%d",&t);
    while(t--){
    
    
        int i=1;
        cin>>n>>k;
        if(n==k) cout<<1<<endl;
        else if(n<k){
    
    
            if(k%n==0) cout<<k/n<<endl;
            else cout<<k/n+1<<endl;
        }
        else{
    
    
            if(n%k==0) cout<<1<<endl;
            else cout<<2<<endl;
        }
    }
}

B. Inflation

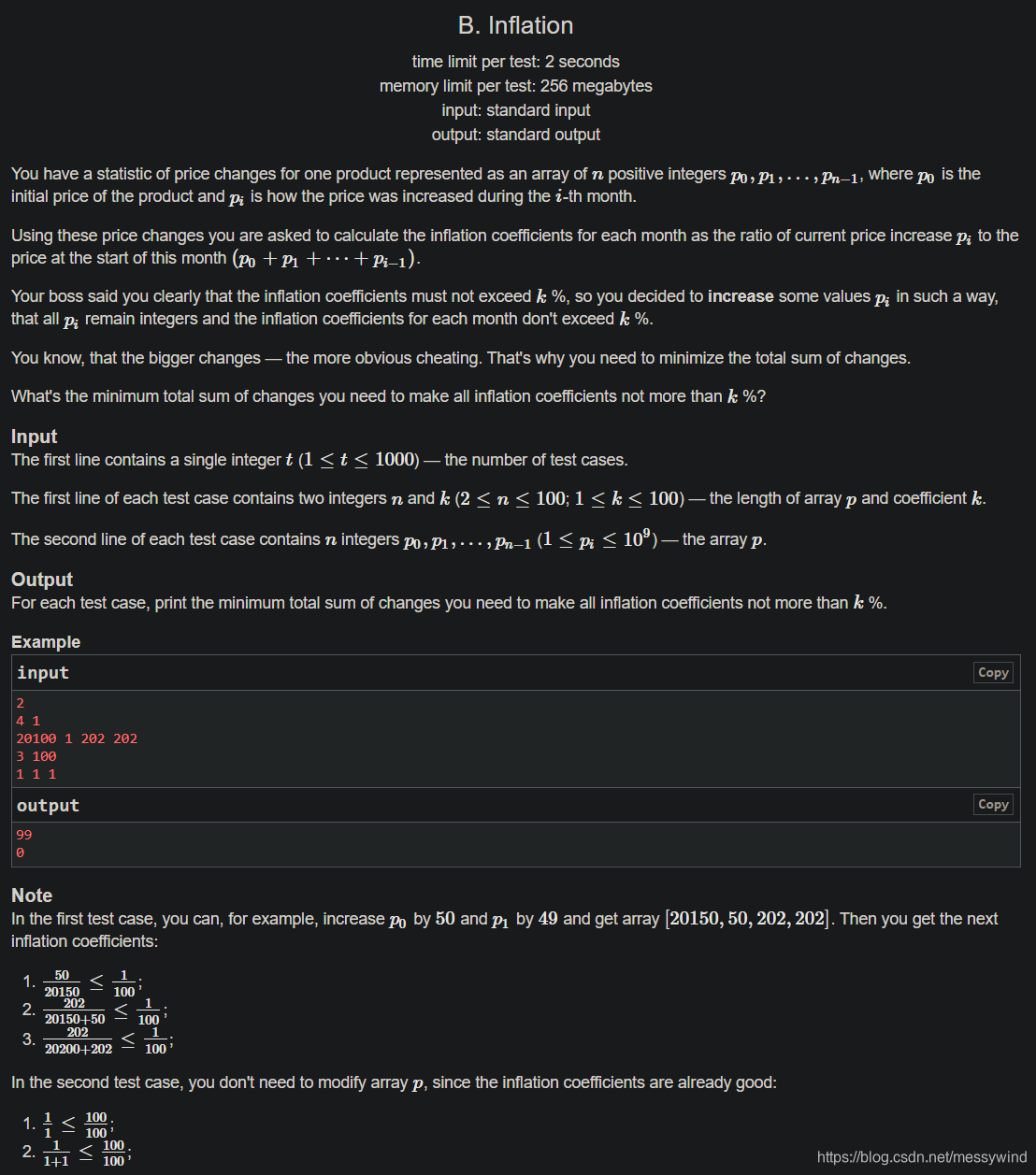
分析： 贪心做法：每次检查比例是不是超过$k$%，如果超过就让分母变为$a/(k$%$)$即$a\ast 100/k$，然后与原来的总和做差更新一下答案就可以了。注意在判断的时候要尽量避免小数，所以两边乘法移项。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=105;
int t,n,k;
long long a,s;
int main(){
    
    
    cin>>t;
    while(t--){
    
    
        long long int res=0;
        cin>>n>>k;
        for(int i=0;i<n;i++){
    
    
            cin>>a;
            if(!i) s=a;
            else{
    
    
                if(100*a>k*s){
    
    
                    long long delta=(100*a-k*s+k-1)/k;
                    res+=delta;
                    s+=delta;
                }
                s+=a;
            }
        }
        cout<<res<<endl;
    }
}