全部笔记的汇总贴(视频也有传送门):中科大-凸优化
一、二次函数
f : R n → R d o m f = R n f:\R^n\rightarrow\R\;\;\;\;\;\; dom f=\R^n f:Rn→Rdomf=Rn
f ( x ) = 1 2 X T P X + δ T X + r , P ∈ S n , δ ∈ R n , r ∈ R f(x)=\frac12X^TPX+\delta^TX+r,\;\;\;P\in S^n,\delta\in\R^n,r\in\R f(x)=21XTPX+δTX+r,P∈Sn,δ∈Rn,r∈R
∇ 2 f ( x ) = P \nabla^2f(x)=P ∇2f(x)=P正定 ⇔ \Leftrightarrow ⇔凸函数
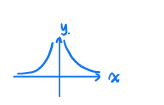
f ( x ) = 1 x 2 x ≠ 0 , x ∈ R f(x)=\frac1{x^2}\;\;\;x\neq0,x\in\R f(x)=x21x=0,x∈R
f ′ ( x ) = 6 x − 4 > 0 f'(x)=6x^{-4}>0 f′(x)=6x−4>0
定义域不是凸集,不是凸函数
二、仿射函数
f ( x ) = A x + b ∇ 2 f ( x ) = 0 n ∗ n ⪰ 0 f(x)=Ax+b\;\;\;\;\;\;\nabla^2f(x)=0_{n*n}\succeq0 f(x)=Ax+b∇2f(x)=0n∗n⪰0
既是凸的又是凹的
三、指数函数
f ( x ) = e a x , x ∈ R f ′ ( x ) = a e a x f ′ ′ ( x ) = a 2 e a x ≥ 0 f(x)=e^{ax},x\in\R\\f'(x)=ae^{ax}\;\;\;f''(x)=a^2e^{ax}\ge0 f(x)=eax,x∈Rf′(x)=aeaxf′′(x)=a2eax≥0
四、幂函数
f ( x ) = x a , x ∈ R + + f ′ ( x ) = a x a − 1 f ′ ′ ( x ) = a ( a − 1 ) x a − 2 ∇ 2 f ( x ) { ≥ 0 a ≥ 1 或 a ≤ 0 凸 ≤ 0 0 ≤ a ≤ 1 凹 f(x)=x^a,x\in\R_{++}\\f'(x)=ax^{a-1}\;\;\;f''(x)=a(a-1)x^{a-2}\\\nabla^2f(x)\left\{ \begin{array}{l} \ge0\;\;\;\;a\ge1或a\le0\;\;凸\\ \\\le0\;\;\;0\le a\le1\;\;\;凹 \end{array} \right. f(x)=xa,x∈R++f′(x)=axa−1f′′(x)=a(a−1)xa−2∇2f(x)⎩⎨⎧≥0a≥1或a≤0凸≤00≤a≤1凹
五、绝对值的幂函数
f ( x ) = ∣ x ∣ P , x ∈ R f ′ ( x ) = { P x P − 1 x ≥ 0 − P ( − x ) P − 1 x < 0 f ′ ′ ( x ) = { P ( P − 1 ) x P − 2 x ≥ 0 P ( P − 1 ) ( − x ) P − 2 x < 0 f(x)=|x|^P,x\in\R\\f'(x)=\left\{ \begin{array}{l} Px^{P-1}\;\;\;\;\;\;x\ge0\\ \\-P(-x)^{P-1}\;\;x<0 \end{array} \right. \\f''(x)=\left\{ \begin{array}{l} P(P-1)x^{P-2}\;\;\;\;\;\;x\ge0\\ \\P(P-1)(-x)^{P-2}\;\;x<0 \end{array} \right. f(x)=∣x∣P,x∈Rf′(x)=⎩⎨⎧PxP−1x≥0−P(−x)P−1x<0f′′(x)=⎩⎨⎧P(P−1)xP−2x≥0P(P−1)(−x)P−2x<0
P > 1 时 , f ( x ) 为 凸 P = 1 时 , f ( x ) = ∣ x ∣ 为 凸 P < 1 时 , 无 结 论 P>1时,f(x)为凸\\P=1时,f(x)=|x|为凸\\P<1时,无结论 P>1时,f(x)为凸P=1时,f(x)=∣x∣为凸P<1时,无结论
六、对数函数
f ( x ) = log x x ∈ R + + f ′ ( x ) = 1 x f ′ ′ ( x ) = − 1 x 2 < 0 f(x)=\log x\;\;\;\;\;x\in\R_{++}\\f'(x)=\frac1x\;\;\;\;f''(x)=-\frac1{x^2}<0 f(x)=logxx∈R++f′(x)=x1f′′(x)=−x21<0
严格凹函数
七、负熵
f ( x ) = x log x x ∈ R + + f ′ ( x ) = 1 + log x f ′ ′ ( x ) = 1 x > 0 f(x)=x\log x\;\;\;\;\;\;x\in\R_{++}\\f'(x)=1+\log x\;\;\;\;\;\;f''(x)=\frac1x>0 f(x)=xlogxx∈R++f′(x)=1+logxf′′(x)=x1>0
严格凸函数
八、范数
R n \R^n Rn空间的范数 P ( x ) , x ∈ R n P(x),x\in\R^n P(x),x∈Rn
- P ( a x ) = ∣ a ∣ P ( x ) P(ax)=|a|P(x) P(ax)=∣a∣P(x)
- P ( x + y ) ≤ P ( x ) + P ( y ) P(x+y)\le P(x)+P(y) P(x+y)≤P(x)+P(y)
- P ( x ) = 0 ⇔ x = 0 P(x)=0\Leftrightarrow x=0 P(x)=0⇔x=0
∀ x , y ∈ R n , ∀ 0 ≤ θ ≤ 1 \forall x,y\in\R^n,\forall 0\le\theta\le1 ∀x,y∈Rn,∀0≤θ≤1
P ( θ x + ( 1 − θ ) y ) ≤ P ( θ x ) + P ( ( 1 − θ ) y ) = θ P ( x ) + ( 1 − θ ) P ( y ) P(\theta x+(1-\theta)y)\le P(\theta x)+P((1-\theta)y)=\theta P(x)+(1-\theta)P(y) P(θx+(1−θ)y)≤P(θx)+P((1−θ)y)=θP(x)+(1−θ)P(y)
是凸函数
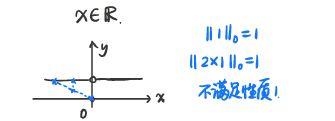
九、零范数
∣ ∣ x ∣ ∣ 0 = ||x||_0= ∣∣x∣∣0=非零元素数目(不是凸函数)
十、极大值函数
f ( x ) = max { x 1 , ⋯ , x n } , x ∈ R n f(x)=\max\{x_1,\cdots,x_n\},x\in\R^n f(x)=max{
x1,⋯,xn},x∈Rn
f ( θ x + ( 1 − θ ) y ) = max { θ x i + ( 1 − θ ) y i , i = 1 , ⋯ , n } ≤ θ max { x i , i = 1 , ⋯ , n } + ( 1 − θ ) max { y i , i = 1 , ⋯ , n } = θ f ( x ) + ( 1 − θ ) f ( y ) f(\theta x+(1-\theta)y)=\max\{\theta x_i+(1-\theta)y_i,i=1,\cdots,n\}\\\le\theta\max\{x_i,i=1,\cdots,n\}+(1-\theta)\max\{y_i,i=1,\cdots,n\}\\=\theta f(x)+(1-\theta)f(y) f(θx+(1−θ)y)=max{
θxi+(1−θ)yi,i=1,⋯,n}≤θmax{
xi,i=1,⋯,n}+(1−θ)max{
yi,i=1,⋯,n}=θf(x)+(1−θ)f(y)
min x max y f ( x , y ) \min_x\max_y f(x,y) xminymaxf(x,y)
凸问题