全部笔记的汇总贴(视频也有传送门):中科大-凸优化
一、凸集(Convex Set)
仿射集一定是凸集
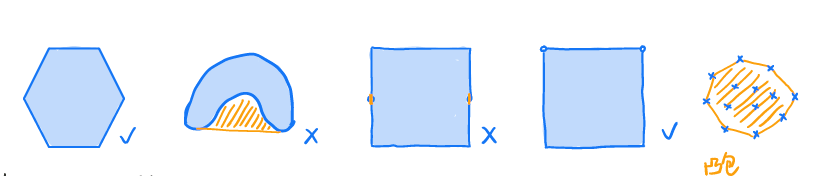
凸集(Convex Set):一个集合 C C C是凸集,当任意两点之间的线段仍在 C C C内。
C C C为凸集 ⇔ \Leftrightarrow ⇔ ∀ x 1 , x 2 ∈ C , ∀ θ , θ ∈ [ 0 , 1 ] , θ x 1 + ( 1 − θ ) x 2 ∈ C \forall x_1,x_2\in C,\forall\theta,\theta\in[0,1],\theta x_1+(1-\theta)x_2\in C ∀x1,x2∈C,∀θ,θ∈[0,1],θx1+(1−θ)x2∈C
凸组合: θ 1 x 1 + ⋯ + θ k x k , θ 1 , ⋯ θ k ∈ R , θ 1 + ⋯ + θ k = 1 , θ 1 , ⋯ , θ k ∈ [ 0 , 1 ] \theta_1x_1+\cdots+\theta_kx_k,\theta_1,\cdots\theta_k\in\R,\theta_1+\cdots+\theta_k=1,\theta_1,\cdots,\theta_k\in[0,1] θ1x1+⋯+θkxk,θ1,⋯θk∈R,θ1+⋯+θk=1,θ1,⋯,θk∈[0,1]
C C C为凸集 ⇔ \Leftrightarrow ⇔任意元素凸组合 ∈ C \in C ∈C
凸包: C ∈ R n C\in\R^n C∈Rn
C o n v C = { θ 1 x 1 + ⋯ + θ k x k ∣ ∀ x 1 , ⋯ , x k ∈ C , ∀ θ 1 , ⋯ , θ k ∈ [ 0 , 1 ] , θ 1 + ⋯ + θ k = 1 } Conv\;\; C=\{\theta_1 x_1+\cdots+\theta_k x_k|\forall x_1,\cdots,x_k\in C,\forall\theta_1,\cdots,\theta_k\in[0,1] ,\theta_1+\cdots+\theta_k=1\} ConvC={
θ1x1+⋯+θkxk∣∀x1,⋯,xk∈C,∀θ1,⋯,θk∈[0,1],θ1+⋯+θk=1}
二、凸锥(Convex Cone)
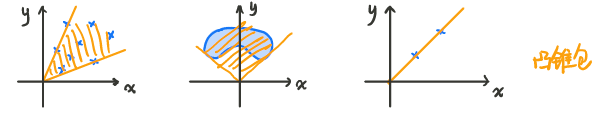
C C C是锥 ⇔ ∀ x ∈ C , θ ≥ 0 , \Leftrightarrow\;\;\forall x\in C,\theta\ge0, ⇔∀x∈C,θ≥0,有 θ x ∈ C \theta x\in C θx∈C
C C C是凸锥 ⇔ ∀ x 1 , x 2 ∈ C , θ 1 , θ 2 ≥ 0 , \Leftrightarrow\;\;\forall x_1,x_2\in C,\theta_1,\theta_2\ge0, ⇔∀x1,x2∈C,θ1,θ2≥0,有 θ 1 x 1 + θ 2 x 2 ∈ C \theta_1 x_1+\theta_2x_2\in C θ1x1+θ2x2∈C

凸锥组合: θ 1 x 1 + ⋯ + θ k x k θ 1 , ⋯ , θ k ≥ 0 \theta_1x_1+\cdots+\theta_kx_k\;\;\theta_1,\cdots,\theta_k\ge0 θ1x1+⋯+θkxkθ1,⋯,θk≥0
凸锥包: x 1 , ⋯ , x k ∈ C { θ 1 x 1 + ⋯ + θ k x k ∣ x 1 , ⋯ , x k ∈ C , θ 1 , ⋯ , θ k ≥ 0 } x_1,\cdots,x_k\in C\;\;\{\theta_1x_1+\cdots+\theta_kx_k|x_1,\cdots,x_k\in C,\theta_1,\cdots,\theta_k\ge0\} x1,⋯,xk∈C{
θ1x1+⋯+θkxk∣x1,⋯,xk∈C,θ1,⋯,θk≥0}
仿射组合 ∀ θ 1 , ⋯ , θ k θ 1 + ⋯ + θ k = 1 \;\;\;\forall\theta_1,\cdots,\theta_k\;\;\;\;\theta_1+\cdots+\theta_k=1 ∀θ1,⋯,θkθ1+⋯+θk=1
凸组合 ∀ θ 1 , ⋯ , θ k θ 1 + ⋯ + θ k = 1 , θ 1 , ⋯ , θ k ∈ [ 0 , 1 ] \;\;\;\;\;\;\forall\theta_1,\cdots,\theta_k\;\;\;\;\theta_1+\cdots+\theta_k=1,\theta_1,\cdots,\theta_k\in[0,1] ∀θ1,⋯,θkθ1+⋯+θk=1,θ1,⋯,θk∈[0,1]
凸锥组合 ∀ θ 1 , ⋯ , θ k θ 1 + ⋯ + θ k ≥ 0 \;\;\;\forall\theta_1,\cdots,\theta_k\;\;\;\;\theta_1+\cdots+\theta_k\ge0 ∀θ1,⋯,θkθ1+⋯+θk≥0
C = { x } θ 1 x + θ 2 x = x 仿 射 集 ∅ 也 是 仿 射 集 C=\{x\}\;\;\;\;\;\;\;\;\;\theta_1x+\theta_2x=x\;\;\;\;\;\;\;\;\;仿射集\;\;\;\;\;\;\;\;\varnothing也是仿射集 C={ x}θ1x+θ2x=x仿射集∅也是仿射集
∅ \varnothing ∅是仿射集、凸集、凸锥。
下一章传送门:中科大-凸优化 笔记(lec5)-几种重要的凸集(上)