抽象代数的代码实现（1） 置换群

前言

之前做了一个四国军棋软件，做到最后发现工作量已经爆炸了，我需要去寻找一个全新的算法来减少工作量，所谓深度学习的算法也许有效果但是对于没有计算资源的人来说并不适用。

我其实是挺喜欢数学的，我总觉得数学上的一些思想方法可能对写代码有所帮助，但是我已经深深意识到自己的大脑不适合去处理数学问题。数学的语言是精确的，数学书籍的作者想表达的意思也是清晰的，对于高智商的人能很容易明白作者的意思，但是对于我这么一个智商一般的人来说，经常感觉到作者想表达的实际意思和自己理解的意思不一样，读起来相当痛苦。另外对于一些高深的数学概念，往往是由很多基础的数学概念叠加而成的，这就需要良好的记忆力，在读到后面时能够十分清楚的记住之前讲述的概念。而我的记忆力很差，当后面定义的新概念需要依赖之前的概念，而我经常忘记之前的概念，甚至草草在脑中代入一个错误的概念，这样接下来读起来就会不知所云。

用C语言去描述数学可能可以解决我阅读数学时的困境，如果代码表达的实际意义和我理解的有偏差，我只需要debug一下，去追踪到底代码哪一行跟自己的理解不一样，从而纠正自己错误的理解。另外一些概念是由很多其他概念组成的，在C语言中这些概念可以理解成函数，借助eclipse这样的开发环境，对于我不理解的概念，我可以跳转到这个函数中再来仔细研究，也可以很快的知道各种概念之间的区别和联系，只要比较对应代码的形式和运行结果就可以知道了。

为了处理的简单和方便，这里会忽略掉一些数学上的严谨性，也不是很注重软件工程的设计，目的主要是提取数学的思想，把一些抽象的概念实例化，从而能更好的理解数学的结构，使数学概念能够通过清晰的代码步骤表现出来。我打算研究抽象代数、组合数学、数理逻辑这三方面的内容，先从抽象代数开始。参考的教材是E.Artin的《伽罗华理论》，再随便配上一本抽象代数或近世代数的书。

1 置换群

群是代数中最基本的概念，而置换群是一种最基本的群，群的概念就是从置换中诞生的，所以先来研究置换群。

1.1 置换

先来定义置换的概念，这里不用数学语言来精确定义，只举实际例子把这个概念说的相对明白就可以了。

现在有一个5元排列（1 2 3 4 5），我们把这排列中的5个元素随便调换一下顺序就可以得到另外一个排列了，比如把2和4交换，1和3交换得到另一个排列（3,4,1,2,5），我们可以把置换用映射表示

$$f=\{\begin{array}{rl}1\to & 3\\ 2\to & 4\\ 3\to & 1\\ 4\to & 2\\ 5\to & 5\end{array}$$
简记为
$$\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 3& 4& 1& 2& 5\end{array}\right)$$

还有一种更简单的记法，例如把（1 2 3 4 5）的这个排列的每个元素都向左移动一个位置得到置换
$$\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 2& 3& 4& 5& 1\end{array}\right)$$
这种置换称作轮换，反复映射后可以得到1->2->3->4->5->1,可以直接用轮换中的任一个排列表示即（1 2 3 4 5）
每一个置换都可以表示成一些轮换的组合，例如
$$\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 3& 4& 1& 2& 5\end{array}\right)$$
可以表示为(1 3)(2 4)(5),即1和3轮换，2和4轮换，5不变，寻找轮换的方法是:
1->3->1,2->4->2,从起始位置开始反复映射，回到自身就是一个轮换。

1.2 群

群是由一个集合中的元素比如集合A={a,b,c,d…}和运算{ $\cdot$}组成的，要注意的是集合中的元素不一定是数字，运算也不一定是乘法，集合和运算具体代表什么需要你自己定义。这些元素的运算必须满足下面4个条件才能称作群

1. 运算封闭，即$a\cdot b$的结果仍在A中
2. 结合律，即$(a\cdot b)\cdot c=a\cdot (b\cdot c)$
3. 有单位元e，即 对于任意的a，存在单位元e使得 $e\cdot a=a$
4. 有左逆元，即对于任意的a，存在b满足$b\cdot a=e$,那么b叫做a的左逆元

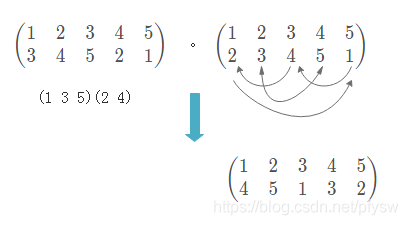
一般来说群并没有规定运算要满足交换律，下面来说明上面定义的置换是群，首先定义置换的运算{ $\cdot$}如下，例如（1 2 3 4 5）$\cdot$ (1 3)(2 4)(5)的计算结果如下

即
$$\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 2& 3& 4& 5& 1\end{array}\right)\cdot \left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 3& 4& 1& 2& 5\end{array}\right)=\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 4& 5& 2& 3& 1\end{array}\right)$$

接下来将用代码证明置换满足群的4条性质，证明第1条性质时需要对置换的概念做一些额外的说明，并写一个函数判断这个元素是不是置换，这个性质是显然满足的，并且写成代码并不会更加清晰所以略去，所以主要证明的是第2,3,4条性质

2 代码实现

2.1 数据结构

首先需要定义一个代数系统的数据结构，初步定义如下

typedef struct OperateSys OperateSys;
struct OperateSys
{
    
    
    void *pBaseEle;//单位元
    int (*xIsEqual)(void *, void *);//判断2个元素是否相等
    void *(*xGen)(int iNum);//根据给定的自然数生成集合中的元
    void *(*xInvEle)(void *);//给定一个元素生成逆元
    void *(*xRecursiveGen)(void *pEle);//根据一个元素递归生成下一个元素，暂时不用
    void *(*xOperat)(void *, void *);//运算
    void *(*xConjOperat)(void *, void *);//共轭运算，这个运算下面会特别说明
};

在实现置换群的代数系统时，首先要定义置换元素的结构

typedef struct FivePerm
{
    
    
    u8 aNum[5];
}FivePerm;

下面来新建一个置换群的OperateSys的对象

 OperateSys *PermutationObj(void)
{
    
    
  //1->1,2->2,3->3,4->4,5->5作为单位元
    static FivePerm baseItem =
    {
    
    
        .aNum[0] = 1,
        .aNum[1] = 2,
        .aNum[2] = 3,
        .aNum[3] = 4,
        .aNum[4] = 5,
    };

    //函数类型不匹配，加void去警告
    static OperateSys perm =
    {
    
    
        NULL,
        (void*)FivePermEqual,
        (void*)FivePermGen,
        (void*)FivePermInv,
        (void*)FivePermRec,
        (void*)FivePermOp,
        (void*)FivePermOp1,
    };
    perm.pBaseEle = &baseItem;
    return &perm;
}

2.2 置换生成

置换是一个集合，为了实现这个代数运算系统，我们首先要生成置换的所有元素，以5个元素的置换为例，这些元素就是(1 2 3 4 5)的一个全排列，全排列总共有120个，所以输入范围从0~119，生成算法采用的是递归的思想，第1个数字可能的取值为1,2,3,4,5五种，确定第1个数字之后，下面进行递归调用求得剩下4个数字的全排列

//pPerm为初始输入元素,即恒等置换(1)
//left表示置换中最左边的一个元素，
//right表示置换中最右边的一个元素
//要生成的元素的序号
void FivePermTrav(FivePerm *pPerm, int left, int right, int num)
{
    
    
    static int cnt = 0;
    static int RecCnt = 0;
    int i;
    
    //cnt是静态变量，第一次调用递归时先清0
    if( RecCnt==0 )
    {
    
    
        cnt = 0;
    }
    RecCnt++;
    //找到要生成的元素后返回
    if( cnt>num )
    {
    
    
        RecCnt--;
        return;
    }
    //递归结束，找到一个置换
    if( left==right )
    {
    
    
        cnt++;
    }
    else
    {
    
    
        //把子置换中最左边的元素依次与右边每个元素调换继续递归
        for(i=left; i<=right; i++)
        {
    
    
            SwapNum(&pPerm->aNum[i],&pPerm->aNum[left]);
            FivePermTrav(pPerm,left+1,right,num);
           // 已经找到要求得元素就不要继续递归了
            if( cnt>num )
            {
    
    
                break;
            }
            //递归完毕后返回将元素换回来，保持初始状态不变
            SwapNum(&pPerm->aNum[i],&pPerm->aNum[left]);
        }
    }
    RecCnt--;
}
 //
FivePerm *FivePermGen(int num)
{
    
    
    FivePerm *p;
    u8 aInit[5] = {
    
    1,2,3,4,5};
    num = num%120;
    p = malloc(sizeof(FivePerm));
    memcpy(p->aNum,aInit,sizeof(aInit));
    FivePermTrav(p,0,4,num);
    return p;
}

2.3 置换乘法运算

首先来实现1.2节定义的置换乘法运算,这是一个映射运算，只要把第2个输入映射的结果作为第1个参数的下标得到运算结果即可:

FivePerm *FivePermOp(FivePerm *p1, FivePerm *p2)
{
    
    
    FivePerm *p;
    int i,j;
    p = malloc(sizeof(FivePerm));
    memset(p,0,sizeof(FivePerm));

    for(i=0; i<5; i++)
    {
    
    
        j = p2->aNum[i]-1;//获取p2的映射结果
        p->aNum[i] = p1->aNum[j];//将j作为p1的下标     
    }
    return p;
}

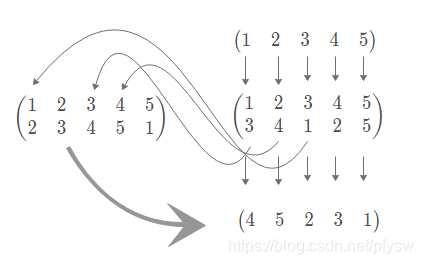
对于置换集合可以再定义一个共轭运算{ $\circ$}，我们来计算 (1 3)(2 4)(5) $\circ$（1 2 3 4 5），其运算结果如下，先写出右元的置换，再把左元写成轮换形式，右元的结果根据左元进行轮换

这里我们发现以下等式成立，记为公式(1)
$$\begin{array}{rl}& \left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 2& 3& 4& 5& 1\end{array}\right)\cdot \left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 3& 4& 1& 2& 5\end{array}\right)\\ =& \left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 3& 4& 1& 2& 5\end{array}\right)\circ \left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 2& 3& 4& 5& 1\end{array}\right)\\ =& \left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 4& 5& 2& 3& 1\end{array}\right)\end{array}\text{\hspace{1em}(1)}$$
即置换的乘法运算与其2个元素交换后的共轭运算是相等的，那么为什么会相等呢，我们先用代码来实现共轭运算，上面举的例子容易搞混，我再举一个典型的例子，

按照上图得到代码的具体实现

FivePerm *FivePermOp1(FivePerm *p1, FivePerm *p2)
{
    
    
    FivePerm *p;
    int i,j;
    p = malloc(sizeof(FivePerm));
    memset(p,0,sizeof(FivePerm));
    for(i=0; i<5; i++)
    {
    
    
        //这里我们要对p2的元素进行置换
        //p2的哪个元素会换到i的位置上
        //根据p1的映射结果就可以得到要置换的位置
        //注意到p2是根据p1的轮换表示来置换的
        j = p1->aNum[i]-1;
        p->aNum[i] = p2->aNum[j];
    }
    return p;
}

对比FivePermOp和FivePermOp1的代码可以看到形式是完全一样的，只不过p1和p2调换个位置，所以我们看到公式（1）是成立的

2.4 置换群的逆运算

以下代码是求左逆元的算法，你可以尝试写写求右逆元的代码，你会发现和求左逆元的代码一模一样，这也就证明了群的左逆元必定是右逆元

FivePerm *FivePermInv(FivePerm *p1)
{
    
    
    FivePerm *p;
    int i,j;
    p = malloc(sizeof(FivePerm));
    memset(p,0,sizeof(FivePerm));

    //无论是求左逆元还是右逆元在代码上的形式是相同的
    for(i=0; i<5; i++)
    {
    
    
        j = p1->aNum[i];
        p->aNum[j-1] = i+1;
    }

    return p;
}

2.5 群的证明

下面证明群的三个性质，这里并非严格按照数学证明，而是我们本身就承认这些性质，通过构造测试用例来明白为什么这些性质是成立的。

结合律

int AssociativeLaw(OperateSys *pOpSys)
{
    
    
    int rc = 0;
    int i,j,k;
    void* pT[7];
    for(i=0; i<10; i++)
    {
    
    
        //随机生成三个伪随机数，并生成3个置换元pT[0]、pT[1]、pT[2]
        for(j=0; j<3; j++)
        {
    
    
            k = FakeRand(i+j*10);
            pT[j] = pOpSys->xGen(k);
        }
        //证明(pT[0]*pT[1])*pT[2]=pT[0]*(pT[1]*pT[2])
        pT[3] = pOpSys->xOperat(pT[1],pT[2]);
        pT[4] = pOpSys->xOperat(pT[0],pT[1]);
        pT[5] = pOpSys->xOperat(pT[0],pT[3]);
        pT[6] = pOpSys->xOperat(pT[4],pT[2]);

        rc = pOpSys->xIsEqual(pT[5],pT[6]);

        for(j=0; j<7; j++)
        {
    
    
            free(pT[j]);
        }
        assert( rc );
    }

    loga("associative ok");
    return rc;
}

有单位元

int HasIdentityEle(OperateSys *pOpSys)
{
    
    
    int rc = 0;
    int i,k;
    void* pEle;
    void* pGen;
    //随机生成10个置换元
    for(i=0; i<10; i++)
    {
    
    
        k = FakeRand(i);
        pGen = pOpSys->xGen(k);
        pEle = pOpSys->xOperat(pOpSys->pBaseEle,pGen);
        //证明单位元和群中的任一元相乘仍然等于该元
        rc = pOpSys->xIsEqual(pGen,pEle);
        free(pGen);
        free(pEle);
        assert( rc );
    }

    loga("identity ok %d",rc);
    return rc;
}

存在可逆元

int HasInvEle(OperateSys *pOpSys)
{
    
    
    int rc = 0;
    int i,k;
    void* pEle;
    void* pGen;
    void* pInv;
    for(i=0; i<10; i++)
    {
    
    
        k = FakeRand(i+2);
        pGen = pOpSys->xGen(k);
        //随机生成10个元并根据pOpSys->xInvEle生成 pInv
        pInv = pOpSys->xInvEle(pGen);
        //证明pInv就是可逆元
        pEle = pOpSys->xOperat(pGen,pInv);
        rc = pOpSys->xIsEqual(pOpSys->pBaseEle,pEle);
        free(pGen);
        free(pEle);
        free(pInv);
        assert( rc );
    }

    loga("inv ok %d",rc);
    return rc;
}

3参考代码

https://github.com/pfysw/CMath