Factorization Machines模型整理

介绍

• FM 模型的参数支持非常稀疏的特征，而 SVM 等模型不行
• FM 的时间复杂度为 $O(n)$，并且可以直接优化原问题的参数，而不需要依靠支持向量或者是转化成对偶问题解决
• FM 是通用的模型，可以适用于任何实数特征的场景，其他的模型不行

FM模型

引入

在线性回归上，把特征进行二项组合后，
$$\hat{y}=w_0+\sum _{i=1}^n{w}_i{x}_i+\sum _{i=1}^{n-1}\sum _{j=i+1}^n{w}_{ij}{x}_i{x}_j\text{\hspace{1em}(1)}$$ 对于 n 维特征，共需要 $C_n^2$ 个，即 $\frac{n(n-1)}{2}$

隐向量

FM 模型引入了矩阵 V，矩阵 V 是一个$n\times k$ 的二维矩阵。这里的 k 是我们设置的参数，一般不会很大，比如 16、32 之类。对于特征每一个维度 $i$，我们都可以找到一个 $v_i$，它表示一个长度为 k 的向量。

那原来的 $w_{ij}$ 由 $v_i$ 和 $v_j$ 计算得到
$$w_{ij}=v_i^T{v}_j\text{\hspace{1em}(2)}$$ 参数量为 $n\times k$，k 是一个常数，所以就是 $O(n)$

式 (1) 改写为
$$\hat{y}=w_0+\sum _{i=1}^n{w}_i{x}_i+\sum _{i=1}^{n-1}\sum _{j=i+1}^n{v}_i^T{v}_j{x}_i{x}_j\text{\hspace{1em}(3)}$$ 当 k 足够大时，可以得到 $W=V\cdot V^T$，矩阵 V 可以看作对 W 做了一个因子分解

运用中，不用设置很大的 k，一是可能没有足够多的样本训练这么多参数，二是限制 k 一定程度提升 FM 模型的泛化能力

最后，FM 引入的隐向量可看作 embedding 的方式

优化

式 (3) 的计算复杂度是 $O(n^2)$，

$$\begin{array}{rl}& \sum _{i=1}^n\sum _{j=i+1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩x_i{x}_j\\ =& \frac{1}{2}\left(\sum _{i=1}^n\sum _{j=1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩x_i{x}_j-\sum _{i=1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_i⟩x_i{x}_i\right)\\ =& \frac{1}{2}\left(\sum _{i=1}^n\sum _{j=1}^n\sum _{f=1}^k{v}_{i,f}{v}_{j,f}{x}_i{x}_j-\sum _{i=1}^n\sum _{f=1}^k{v}_{i,f}{v}_{i,f}{x}_i{x}_i\right)\\ =& \frac{1}{2}\sum _{f=1}^k\left(\left(\sum _{i=1}^n{v}_{i,f}{x}_i\right)\left(\sum _{j=1}^n{v}_{j,f}{x}_j\right)-\sum _{i=1}^n{v}_{i,f}^2{x}_i^2\right)\\ =& \frac{1}{2}\sum _{f=1}^k\left({\left(\sum _{i=1}^n{v}_{i,f}{x}_i\right)}^2-\sum _{i=1}^n{v}_{i,f}^2{x}_i^2\right)\end{array}\text{\hspace{1em}(4)}$$ 这就相当于一个对称矩阵，先减掉对角线元素，再取 1/2

对比

Linear SVM

$$\hat{y}(\mathbf{X})=w_o+w_u+w_i\text{\hspace{1em}(2)}$$ $x_j=1$ if and only if $j=u$ or $j=i$.

the parameters can be estimated well even under sparsity.
However, the empirical prediction quality typically is low

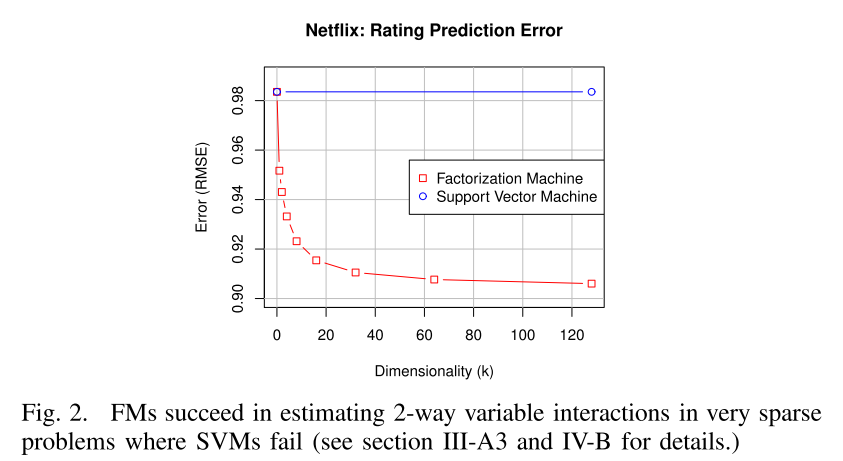
Polynomial SVM

$$\hat{y}(\mathbf{x})=w_0+\sqrt{2}\left(w_u+w_i\right)+w_{u,u}^{(2)}+w_{i,i}^{(2)}+\sqrt{2}{w}_{u,i}^{(2)}\text{\hspace{1em}(5)}$$

总结

(1) FMs are able to estimate parameters under huge sparsity, (2) the model equation is linear and depends only on the model parameters and thus (3) they can be optimized directly in the primal.
(1) FM能够在非常稀疏的情况下估计参数；(2) 模型方程是线性的，并且仅取决于模型参数，因此 (3) 可以直接对其进行优化。

simply by using the right indicators in the input feature vector, FMs are identical or very similar to many of the specialized state-of-the-art models
只需在输入特征向量中使用正确的指示器，FM 就可以与许多专门的最新模型相同或非常相似

代码

import torch
from torch import nn

ndim = len(feature_names)
k = 16

class FM(nn.Module):
    def __init__(self, dim, k):
        super(FM, self).__init__()
        self.dim = dim
        self.k = k
        self.linear = nn.Linear(self.dim, 1, bias=True)
        # 初始化V矩阵
        self.v = nn.Parameter(torch.rand(self.dim, self.k) / 100)
        
    def forward(self, x):
        y_linear = self.linear(x)
        # 二次项
        y_quadradic = 0.5 * torch.sum(torch.pow(torch.mm(x, self.v), 2) - torch.mm(torch.pow(x, 2), torch.pow(self.v, 2)))
        # 输出
        return torch.sigmoid(y_linear+ y_quadradic)

fm = FM(ndim, k)