Xiaojie雷达之路---毫米波雷达基础知识---一些系统设计的话题

本篇文章主要是介绍毫米波雷达的基础知识中的系统设计，主要包含三个知识点

2D-FFT的过程
在设计帧的时候，根据一些参数进行的折中
雷达距离的等式

2D-FFT

range-FFT

雷达处理接收天线接收回来的数据，对每一个接收回来的chirp做range-fft，然后range-fft处理后的数据按行存储到L3或DDR中，由于range-fft对应的频率，距离与中频成正比，因此可以将x轴绘制为距离轴，如下图：

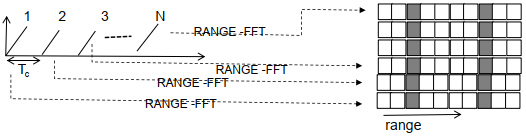
在上面的图中，在距离维度上的range=3和range=8的距离处有物体，但是有几个物体不知道，只是知道雷达前方有物体，

注意：

1. 在大多数雷达的实现中，range-fft是在将ADC样本存储到内存之前完成的

doppler-FFT

在执行完range-fft之后，要在chirp index方向上做doppler-fft，做doppler-fft的时候，要将数据从L3或DDR内存中取出，然后再执行doppler-fft，由于dopper-fft对应离散角频率，离散角频率与速度成正比，因此可以将y轴绘制为速度轴。

如下图：

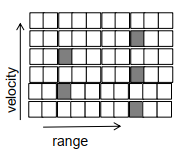
对做了range-fft的数据做doppler-fft，会发现在距离为range=3处有两个物体，速度分别为1和4，在range=8处有三个物体，速度分别为1、3和5。

注意：

1. 只有一个frame中的全部chirp做了range-fft之后才可以执行doppler-fft，因此系统中必须有足够的存储器来存储执行range-fft之后的数据

设计chirp的参数要求

最大速度：
$v_{max}=\frac{\lambda }{4T_c}\Rightarrow T_c=\frac{\lambda }{4v_{max}}$
$Tc$的取值受限于雷达可测的最大速度
速度分辨率：
$v_{res}=\frac{\lambda }{2T_f}\Rightarrow T_f=\frac{\lambda }{2v_{res}}$
$T_f$的取值受限于雷达可测的速度分辨率
距离分辨率：
$d_{res}=\frac{c}{2B}\Rightarrow B=\frac{c}{2d_{res}}$
$B$的取值受限于雷达可测的距离分辨率

由于chirp的带宽和持续时间确定，那么意味着chirp的斜率S也就确定

在实际的确定参数的过程中，可能会受到雷达设备自身的限制

扫描二维码关注公众号，回复： 12676052 查看本文章

1. 设备可能不支持最大的中频带宽，由于$f_{I{F}_{m}ax}=\frac{S2d_{max}}{c}$，因此$S$和$d_{max}$之间要有一个折中，$d_{max}$增大，$S$减小
2. 设备要能够生成所需要的chirp的斜率
3. 在两个相邻的chirp之间，指定的idle time，也需要满足设备
4. 设备必须有足够的内存来存储frame中全部的chirps

假设$T_c$已经由$v_{max}$决定，短距离的雷达的chirp的斜率更高，因此有一个更大的带宽(B)，有更好的距离分辨率，长距离的雷达的chirp的斜率更低，因此有一个较小的带宽(B)，距离分辨率就会变差。

雷达的距离方程

ADC的采样率会限制雷达探测的最远距离，还有一个因素是最大的距离物体的发射信号应具有足够的强度，才能够被雷达检测到

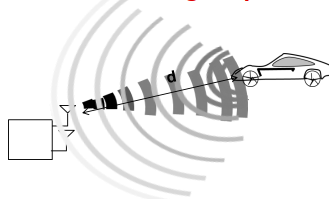
雷达辐射的密度公式为：$\frac{P_t{G}_{TX}}{4\pi d^2}W/m^2$，$P_t$为雷达的发射功率，在空间中，功率密度随距离的平方增加而不断减小，$G_{TX}$为发射天线的增益。
当信号碰到物体，反射的功率为：$\frac{P_t{G}_{TX}\sigma }{4\pi d^2}W$，$\sigma$是物体的发射截面积(Radar Cross Section of the Target，RCS)
在接收天线处的接收功率密度为：$\frac{P_t{G}_{TX}\sigma }{(4\pi {)}^2{d}^4}W/m^2$，在信号返回的空间中，功率密度随距离的平方增加而不断减小
在接收天线处的捕获的功率为：$\frac{P_t{G}_{TX}\sigma A_{RX}}{(4\pi {)}^2{d}^4}W$，$A_{RX}=\frac{G_{RX}{\lambda }^2}{4\pi }$，进行替换，得到$\frac{P_t{G}_{TX}\sigma G_{RX}{\lambda }^2}{(4\pi {)}^3{d}^4}W$，$A_{RX}$是接收天线的有效的孔径的面积

接收器是否能够看到目标不仅取决于接收到信号的功率，还取决于信号能量于噪声能量的比率，也就是信噪比(SNR)
公式：$SNR=\frac{\sigma P_t{G}_{TX}{G}_{RX}{\lambda }^2{T}_{meas}}{(4\pi {)}^3{d}^{4}kTF}$
$T_{meas}$是总共的测量时间，$T_{meas}=N{T}_c$，N表示有多少个chirp，$T_c$是说明每个chirp持续的时间
kT是接收器的热噪声，k是玻尔兹曼常数，T是天线的温度

检测物体所需要的最小信噪比$SN{R}_{min}$，在距离速度图中检测到的信噪比只要小于$SN{R}_{min}$就不会被视为有效的目标，是漏检(missed detection)和虚警(false alarm)的折衷。典型的值的范围是15dB~20dB。

当指定了$SN{R}_{min}$，最大距离$d_{max}$就可以确定：
$d_{max}=(\frac{\sigma P_t{G}_{TX}{G}_{RX}{\lambda }^2{T}_{meas}}{(4\pi {)}^{3}SN{R}_{min}kTF}{)}^{\frac{1}{4}}$

参考文献：

1. 《mmwaveSensing-FMCW-offlineviewing》