Xiaojie雷达之路---毫米波雷达基础知识---中频信号的相位

本篇文章主要介绍毫米波雷达的基础知识中的中频信号的相位

傅里叶变换的快速回顾

傅里叶变换是将一个信号从时域中转换到频域中，在时域中的一个正弦信号将在频域中产生一个峰值，在大多数情况下，在频域中的一个信号是一个复数(每个值是一个振幅和相位的向量)，表示为$A{e}^{j\theta }$

在频域中峰值的相位等于正弦函数的初始相位

中频信号的相位

上一篇文章中提到，雷达前方的一个物体会产生一个中频信号，频率为$\frac{S2d}{c}$，上一篇文章主要是分析中频信号在频率时间图(f-t)中的显示。

本篇文章只要是分析中频信号在幅度时间图(A-t)中的显示

上图中第一个信号是TX chirp，第二个信号是RX chirp，第三个信号是IF signal，混频器的作用就是将TX信号和RX信号的频率和相位分别相减，得到中频信号的频率和相位

当RX chirp的时间延迟$\Delta \tau$的时候，会出现下图的情况

上图显示A和D之间的相位差为$\Delta \Phi =2\pi f_c\Delta \tau =\frac{4\pi \Delta d}{\lambda }$，这个相位也是C和F之间的相位差

推导公式：$\Delta \Phi =2\pi f_c\Delta \tau =\frac{4\pi \Delta d}{\lambda }$
已知：$\Delta \tau =\frac{2\Delta d}{c}，\lambda =\frac{c}{f}$
进行替换得到：$\Delta \Phi =2\pi f_c\Delta \tau =\frac{4\pi \Delta d}{\lambda }$

中频信号为$Asin(2\pi ft+{\varphi }_o)，f=\frac{S2d}{c}，\Delta =\frac{4\pi \Delta d}{\lambda }$，这个式子说明，在雷达前面的单个物体，中频信号的频率与物体的距离成正比，物体的起始相位随距离的微小变换$\Delta d$以线性方式进行改变

中频信号对物体微小位移的灵敏度

中频信号为$Asin(2\pi ft+{\varphi }_o)，f=\frac{S2d}{c}，\Delta =\frac{4\pi \Delta d}{\lambda }$

假设chirp如下图所示，雷达前面有一个物体，并且移动1mm会发生什么情况？

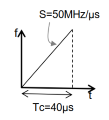
对于77GHz的雷达，1mm相当于$\frac{\lambda }{4}$
$\lambda =\frac{c}{f}=\frac{3\ast 10^8}{77\ast 10^9}=3.89mm$
因此，1mm相当于$\frac{\lambda }{4}$

雷达前方的物体移动1mm，相位的变化为$\Delta \varphi =\frac{4\pi \Delta d}{\lambda }=\pi =180°$，频率变化为$\Delta f=\frac{S2\Delta d}{c}=\frac{50\ast 10^{12}\ast 2\ast 1\ast 10^{-3}}{3\ast 10^8}=333Hz$。333Hz看起来是一个很大的数字，但在观测窗口内仅仅对应的是$\Delta f{T}_c=333\ast 40\ast 10^{-6}=0.013cycles$，这个改变在频率谱中是不可分辨的

如何2个chirps来对一个物体的速度进行测量

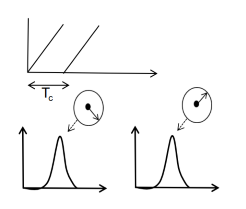
• 发送两个时间间隔为$T_c$的chirp
• 对接收回来的信号做range-FFTs会在相位的位置产生峰值，但是有不同的相位
• 相位差($\omega$)对应于物体移动的距离$v{T}_c$，v是物体的速度，$T_c$是时间

因此有下列公式：
$\omega =\frac{4\pi v{T}_c}{\lambda }$
推出$v=\frac{\lambda \omega }{4\pi T_c}$

因此两个连续的chirp可以用来估计一个目标的速度

测量一个振动的物体

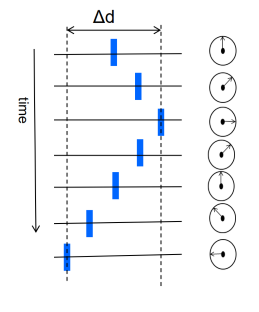
相位随时间的变换可以用来估计振动物体的振幅和周期性

参考文献：

1. 《mmwaveSensing-FMCW-offlineviewing》