前言:
逻辑回归在工业上运用广泛,本文只着重讲解逻辑回归的推导过程,具体的实例还需读者自己去寻找;
–-----------------------------------------------------------------------------—------------------------
–-----------------------------------------------------------------------------—------------------------
一、逻辑回归与线性回归:
逻辑回归是一种广义线性回归(generalized linear model),因此它与多重线性回归有一些异同点:
- 相同点:它们的模型形式基本上相同,都具有 w ’ x + b w’x+b w’x+b,其中 w w w和 b b b是待求参数, w w w是系数矩阵, b b b是偏置项;
- 不同点:多重线性回归是直接将 w ’ x + b w’x+b w’x+b的结果作为因变量 y y y,即 y = w ’ x + b y=w’x+b y=w’x+b; 而逻辑回归添加了一个中间函数 L ( x ) L(x) L(x),将 w ’ x + b w’x+b w’x+b通过 L ( x ) L(x) L(x)映射成一个隐状态 p p p,即 p = L ( w ’ x + b ) p=L(w’x+b) p=L(w’x+b),然后再根据 p p p与 1 − p 1-p 1−p的大小决定因变量 y y y的值;
如果这个中间函数 L ( x ) L(x) L(x)是Logistic型函数(Logistic型函数/曲线即为常见的S形函数),则这个回归分析就是逻辑回归(Logistic Regression,LR);而如果这个中间函数 L ( x ) L(x) L(x)是多项式函数,那么这个回归分析就是多项式回归;
–-----------------------------------------------------------------------------—------------------------
1.1:Logistic型曲线的性质
Logistic型函数/曲线即为常见的S形函数,例:S型函数形如下:
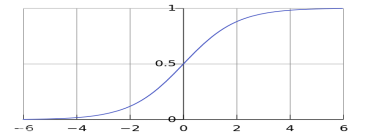
Logistic曲线性质:可将(-∞,+∞)的自变量 x x x压缩到[0, 1]的范围;再结合既定阈值,Logistic函数就可以将连续变化的 x x x值,映射转化为非零即一的因变量的值——这也是由回归到分类的过程;
–-----------------------------------------------------------------------------—------------------------
–-----------------------------------------------------------------------------—------------------------
–-----------------------------------------------------------------------------—------------------------
二、Logistic型函数的一个特例——Sigmod函数:
在Logistic曲线类中,Sigmod函数是具有代表性的一个函数,首先看一下它的表达式:
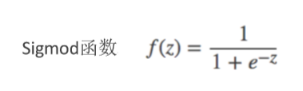
为什么说Sigmod函数是个特例?Sigmod函数的特殊性有以下两点:
- 压缩性:
Sigmod函数能将(-∞,+∞)的自变量 z z z压缩到[0, 1]的范围; - 导数特殊性:
Sigmod函数求导过程如下,可以发现——Sigmod函数的导数=它自身*(1-它自身)
因为在求解系数矩阵 w w w、偏置项 b b b时少不了对原等式进行求导,而Sigmod函数的导数与自身构成关系,这在求解的过程中可以减少运算量。所以上面的压缩性是所有Logistic曲线都具有的性质,而导数特殊性是Sigmod函数被选中的主要因素;

–-----------------------------------------------------------------------------—------------------------
–-----------------------------------------------------------------------------—------------------------
–-----------------------------------------------------------------------------—------------------------
三、逻辑回归原理:(重点)
逻辑回归是在线性回归的基础上发展而来的。线性回归是直接将 w ’ x + b w’x+b w’x+b的结果作为因变量 y y y,即 y = w ’ x + b y=w’x+b y=w’x+b;
而逻辑回归是在线性回归里添加了一个中间函数 L ( x ) L(x) L(x),将 w ’ x + b w’x+b w’x+b先通过 L ( x ) L(x) L(x)映射成一个隐状态 p p p,即 p = L ( w ’ x + b ) p=L(w’x+b) p=L(w’x+b),然后再根据 p p p与 1 − p 1-p 1−p的大小决定最后因变量 y y y的值;
更一般的函数形式如下,自变量 x x x与 z z z的关系是 z = θ ′ x z=θ'x z=θ′x( x x x是训练数据,可以是低维数组也可以是高维向量; θ θ θ是矩阵形式的待定系数)。 z z z再经过中间函数 g ( z ) g(z) g(z)的作用,映射成为 h θ ( x ) h_θ(x) hθ(x)= g ( θ ′ x ) g(θ'x) g(θ′x),这里 h θ ( x ) h_θ(x) hθ(x)相当于因变量 y y y,再将 g ( θ ′ x ) g(θ'x) g(θ′x)换成Sigmod函数就变成下图的第二行等式;

为求解矩阵形式的待定系数 θ θ θ,我们沿用线性回归的最小二乘法——均方误差求极值的方法求取损失的最优解,也就是用预测值和真实值的差值的平方和来估计参数 θ θ θ的优劣,这时就遇到了问题:
3.1、类比线性回归求解系数时遇到的新问题
在线性回归中,均方误差求极值的方法得到的损失函数cost大多是如下右图的凸函数(不是直接的凸函数,也可以经过变换转化成凸函数);而在逻辑回归中也用这种方法得到的损失函数曲线形如左下图,这是一个非凸函数,具有多个局部极小值点,在难以求得全局最小值的情况下,表现并不好。

那有什么方法,能将这个非凸函数的损失函数转化成凸函数呢?
–-----------------------------------------------------------------------------—------------------------
3.2、重新定义损失函数
于是大神们就开始研究了——有没有那种经过Sigmod函数映射后,它的损失函数还是凸函数的函数呢?
大牛们当然是能找到这样的函数的,如下:(y是标签,二分类y ∈ \in ∈{0,1})

解释y = 1的情况,也就是上左图:(y = 0同理)

从损失函数、 h θ ( x ) h_θ(x) hθ(x)函数与 x x x的变化规律说明:上面这个分段函数满足我们对新损失函数的要求——自变量 x x x经过了Sigmod函数映射后得到的损失函数确实是个凸函数;
但新问题也同时出现了——这个新的损失函数由于是个分段函数,在计算的过程中是很复杂的,那有没有什么办法可以将这个分段函数合成一个函数呢?
–-----------------------------------------------------------------------------—------------------------
3.3、解决分段函数问题——极大似然估计
我们采用极大似然估计的方法,将这个分段函数合成一个函数;
–-----------------------------------------------------------------------------—------------------------
这里博主只能粗略的对极大似然估计进行讲解,如果你想要很清楚的看懂下面的理论,建议深入学习
极大似然估计只是一种粗略的数学期望,通过已出现或已观测的结果对总体期望进行估计的一种方法,表达式为 L ( θ ) = p ( y i ∣ X ; θ ) L(θ)=p(y_i|X;θ) L(θ)=p(yi∣X;θ)
假设:某一事件只有两个可能发生的结果: y = 0 , y = 1 y=0,y=1 y=0,y=1
- y = 1 y=1 y=1的概率为: p ( y = 1 ∣ X ; θ ) p(y=1|X;θ) p(y=1∣X;θ)
- y = 0 y=0 y=0的概率为: p ( y = 0 ∣ X ; θ ) p(y=0|X;θ) p(y=0∣X;θ),也等于 1 − p ( y = 1 ∣ X ; θ ) 1-p(y=1|X;θ) 1−p(y=1∣X;θ)
则用极大似然估计,总体期望 L ( θ ) = p ( y i ∣ X ; θ ) = p ( y = 1 ∣ X ; θ ) ∗ p ( y = 0 ∣ X ; θ ) = p ( y = 1 ∣ X ; θ ) ∗ ( 1 − p ( y = 1 ∣ X ; θ ) ) L(θ)=p(y_i|X;θ)=p(y=1|X;θ)*p(y=0|X;θ)=p(y=1|X;θ)*(1-p(y=1|X;θ)) L(θ)=p(yi∣X;θ)=p(y=1∣X;θ)∗p(y=0∣X;θ)=p(y=1∣X;θ)∗(1−p(y=1∣X;θ))
结合上面的分段函数,概率 p p p是满足Sigmod函数变化的,即:
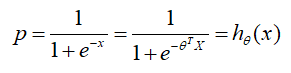
则将概率 p p p换成 h θ ( x ) h_θ(x) hθ(x),极大似然函数就变成如下:
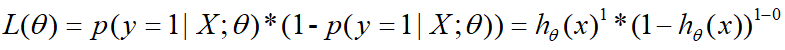
更一般的形式即为:
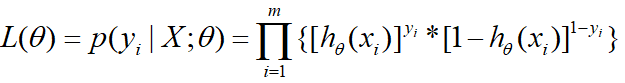
两边再取导数,连乘变成连加就成如下,这个等式在下面就会用到:
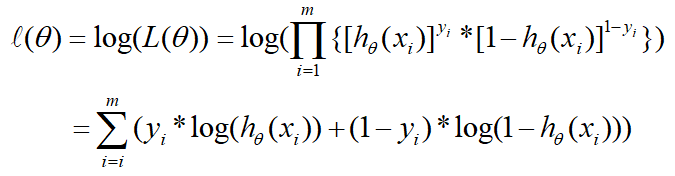
–-----------------------------------------------------------------------------—------------------------
通过极大似然估计的方法,将上面的分段函数转化成为了一个函数,也就是下面的目标函数:

–-----------------------------------------------------------------------------—------------------------
3.4、确定 θ θ θ的更新公式
我们的终极目标就是求上面这个目标函数的极值点,使用梯度下降法, θ θ θ的更新依据公式如下, α α α是学习率
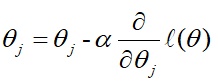
所以需要对θ进行求导:
根据上式,确切的 θ θ θ更新公式即为:
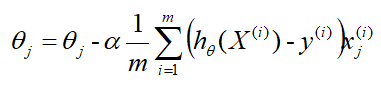
因为式中 α α α是既定的学习率,所以 1 / m 1/m 1/m可以省略,所以最终的 θ θ θ更新公式为:
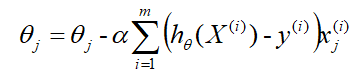
其中
- α α α是学习率;
- h θ ( X ) h_θ(X) hθ(X)是在当前参数 θ θ θ下得到的预测值;
- y y y是真实值;
- x j x_j xj是第 j j j个参与训练的数据, x j x_j xj ∈ \in ∈ X X X
–-----------------------------------------------------------------------------—------------------------
–-----------------------------------------------------------------------------—------------------------
–-----------------------------------------------------------------------------—------------------------
说明:
逻辑回归详细的给出了参数学习的方向,在深度学习中这个思想运用广泛,所以理解其中的算法思路很重要;
–-----------------------------------------------------------------------------—------------------------
–-----------------------------------------------------------------------------—------------------------
–-----------------------------------------------------------------------------—------------------------
补充知识:
Sigmod函数的由来——事件的优势比( o d d s odds odds),那什么是事件的优势比?
- 事件成功的几率 p p p与事件失败的几率 1 − p 1-p 1−p的比值即为事件的优势比: o d d s = p / ( 1 − p ) odds = p/(1-p) odds=p/(1−p)
两边取对数: l n ( o d d s ) = l n ( p / ( 1 − p ) ) ln(odds)=ln(p/(1-p)) ln(odds)=ln(p/(1−p)),求取 p p p, p p p的表达式就是Sigmod函数