各种各样的搜索(⊙ ▽ ⊙)(2)记忆化搜索之章
前言
这周在忙答辩,都没怎么刷题┭┮﹏┭┮
这是答辩的两个小游戏(其实有一些bug ヾ(゚∀゚ゞ)但我懒得改了)
跳一跳
疯狂弹球
后面有时间的话我再补充一些
1、[NOIP2010 提高组] 引水入城
题目描述
在一个遥远的国度,一侧是风景秀美的湖泊,另一侧则是漫无边际的沙漠。该国的行政区划十分特殊,刚好构成一个N 行×M 列的矩形,如上图所示,其中每个格子都代表一座城市,每座城市都有一个海拔高度。
为了使居民们都尽可能饮用到清澈的湖水,现在要在某些城市建造水利设施。水利设施有两种,分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。
因此,只有与湖泊毗邻的第1 行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差,将湖水从高处向低处输送。故一座城市能建造输水站的前提,是存在比它海拔更高且拥有公共边的相邻城市,已经建有水利设施。由于第N 行的城市靠近沙漠,是该国的干旱区,所以要求其中的每座城市都建有水利设施。那么,这个要求能否满足呢?如果能,请计算最少建造几个蓄水厂;如果不能,求干旱区中不可能建有水利设施的城市数目。
输入格式
每行两个数,之间用一个空格隔开。输入的第一行是两个正整数N,M,表示矩形的规模。接下来N 行,每行M 个正整数,依次代表每座城市的海拔高度。
输出格式
两行。如果能满足要求,输出的第一行是整数1,第二行是一个整数,代表最少建造几个蓄水厂;如果不能满足要求,输出的第一行是整数0,第二行是一个整数,代表有几座干旱区中的城市不可能建有水利设施。
输入输出样例
输入 #1
2 5
9 1 5 4 3
8 7 6 1 2
输出 #1
1
1
输入 #2
3 6
8 4 5 6 4 4
7 3 4 3 3 3
3 2 2 1 1 2
输出 #2
1
3
说明/提示
【样例1 说明】
只需要在海拔为9 的那座城市中建造蓄水厂,即可满足要求。
【样例2 说明】
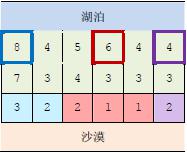
上图中,在3个粗线框出的城市中建造蓄水厂,可以满足要求。以这3个蓄水厂为源头在干旱区中建造的输水站分别用3 种颜色标出。当然,建造方法可能不唯一。
【数据范围】

这道题是我第一次碰到记忆化搜索,这道题的首先我们要判断能否走到最后,仅这部分而言,其实和普通的深搜非常像,然后第二问,其实是我们要学习的新内容:记忆化搜索,因为仅凭借最后搜索的结果返回一个参数是很难解决这个问题的,所以我们要存储搜索的过程,如果走不通,就需要我们输出哪些没有遍历到,所以我们要存储遍历到的点,如果能走通的话,我们要输出最少用几个起始点,所以我们要存储每个起始点能覆盖的最大长度(容易证明,如果能走通的话,每个点能走通的区间都是连续的),然后利用贪心算法,每次我们都选择最合适的起点,看看最少几个起点,输出即可
AC code
#include <bits/stdc++.h>
#pragma GCC optimize(3,"Ofast","inline")
#define ll long long
#define ull unsigned long long
#define re read()
using namespace std;
//速读
inline int read()
{
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){
if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){
x=x*10+ch-48;ch=getchar();}
return x*f;
}
//并查集
int f[1];
int found(int k){
if(f[k] == k){
return k;
}
return f[k] = found(f[k]);
}
//辗转相除法
int gcd(int p,int q){
int t = p % q;
return t==0?q:gcd(q,t);
}
//阶乘
int fac(int k){
int ans = 1;
for(int i = 1; i<= k; i++){
ans *= i;
}
return ans;
}
int r[510][510];
int l[510][510];
bool vis[510][510];
int high[510][510];
int n,m;
inline void dfs(int x, int y){
vis[y][x] = true;
if(x + 1 <= m && high[y][x] > high[y][x+1]){
if(vis[y][x+1] == false){
dfs(x+1,y);
}
l[y][x] = min(l[y][x],l[y][x+1]);
r[y][x] = max(r[y][x],r[y][x+1]);
}
if(x - 1 >= 1 && high[y][x] > high[y][x-1]){
if(vis[y][x-1] == false){
dfs(x-1,y);
}
l[y][x] = min(l[y][x],l[y][x-1]);
r[y][x] = max(r[y][x],r[y][x-1]);
}
if(y + 1 <= n && high[y][x] > high[y+1][x]){
if(vis[y+1][x] == false){
dfs(x,y+1);
}
l[y][x] = min(l[y][x],l[y+1][x]);
r[y][x] = max(r[y][x],r[y+1][x]);
}
if(y - 1 >= 1 && high[y][x] > high[y-1][x]){
if(vis[y-1][x] == false){
dfs(x,y-1);
}
l[y][x] = min(l[y][x],l[y-1][x]);
r[y][x] = max(r[y][x],r[y-1][x]);
}
}
bool flag = false;
int cnt = 0;
int main()
{
ios::sync_with_stdio(false);
n = re;
m = re;
memset(r,0,sizeof(r));
memset(l,0x3f,sizeof(l));
memset(vis,false,sizeof(vis));
for(int i = 1; i <= m; i++){
l[n][i] = i;
r[n][i] = i;
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
high[i][j] = re;
}
}
for(int i = 1; i <= m; i++){
if(!vis[1][i]){
dfs(i,1);
}
}
for(int i =1; i <= m; i++){
if(vis[n][i] == false){
flag = true;
cnt++;
}
}
if(flag){
cout<<"0"<<endl;
cout<<cnt<<endl;
return 0;
}
int left = 1;
while(left <= m){
int maxr = 0;
for(int i = 1; i <= m; i++){
if(l[1][i] <= left){
maxr = max(maxr,r[1][i]);
}
}
cnt++;
left = maxr + 1;
}
cout<<"1"<<endl;
cout<<cnt<<endl;
return 0;
}
2、[USACO08MAR]Cow Travelling S
题目描述
奶牛们在被划分成 N 行 M 列(2≤N,M≤100)的草地上游走, 试图找到整块草地中最美味的牧草。
Farmer John 在某个时刻看见贝茜在位置 (R1,C1),恰好 T(0<T≤15)秒后,FJ 又在位置 (R2,C2) 与贝茜撞了正着。FJ 并不知道在这 T 秒内贝茜是否曾经到过 (R2,C2),他能确定的只是,现在贝茜在那里。
设 S 为奶牛在 T 秒内从 (R1,C1) 走到 (R2,C2) 所能选择的路径总数,FJ 希望有 一个程序来帮他计算这个值。每一秒内,奶牛会水平或垂直地移动 1 单位距离(奶牛总是在移动,不会在某秒内停在它上一秒所在的点)。草地上的某些地方有树,自然,奶牛不能走到树所在的位置,也不会走出草地。
现在你拿到了一张整块草地的地形图,其中 . 表示平坦的草地,* 表示挡路的树。你的任务是计算出,一头在 T 秒内从 (R1,C1) 移动到 (R2,C2) 的奶牛可能经过的路径有哪些。
输入格式
第一行包含 3 个用空格隔开的整数:N,M,T。
接下来 n 行:第 i 行为 M 个连续的字符,描述了草地第 i 行各点的情况,保证字符是 . 和 * 中的一个。
最后一行 4 个整数 R1,C1,R2,C2。
输出格式
输出从(R1,C1) 移动到 (R2,C2) 的方案数。
输入输出样例
输入 #1
4 5 6
...*.
...*.
.....
.....
1 3 1 5
输出 #1
1
说明/提示
奶牛在 6 秒内从 (1,3) 走到 (1,5) 的方法只有一种,绕过她面前的树。
这道题如果我们不采取记忆化搜索,正常去写,输出答案其实不是很困难,就是搜索,计时,到时间看看位置,如果对的话ans++,但这样写如果数据量大一些的话就会TLE。然后我们想到,其实对每个点每个时间我们只需要搜索一次,但在暴力搜索中搜索了很多次,我们存储一下每次搜索的结果的话就可以完成一个类似剪枝的效果,所以找到题的记忆化搜索主要体现在优化上
AC code
#include <bits/stdc++.h>
#pragma GCC optimize(3,"Ofast","inline")
#define re register
#define ll long long
#define ull unsigned long long
#define r read()
using namespace std;
//速读
inline int read()
{
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){
if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){
x=x*10+ch-48;ch=getchar();}
return x*f;
}
//并查集
int f[1];
int found(int k){
if(f[k] == k){
return k;
}
return f[k] = found(f[k]);
}
//辗转相除法
int gcd(int p,int q){
int t = p % q;
return t==0?q:gcd(q,t);
}
//阶乘
int fac(int k){
int ans = 1;
for(int i = 1; i <= k; i++){
ans *= i;
}
return ans;
}
int n,m,t;
bool mp[105][105];
int dp[105][105][20];
int x_begin,y_begin;
int x_end,y_end;
int dfs(int x , int y, int s){
if(dp[y][x][s] != -1){
return dp[y][x][s];
}
if(x == x_end && y == y_end && s == 0){
return 1;
}
if(s < 0){
return 0;
}
int ans = 0;
if(mp[y][x-1]){
ans += dfs(x-1,y,s-1);
}
if(mp[y][x+1]){
ans += dfs(x+1,y,s-1);
}
if(mp[y-1][x]){
ans += dfs(x,y-1,s-1);
}
if(mp[y+1][x]){
ans += dfs(x,y+1,s-1);
}
return dp[y][x][s] = ans;
}
int main()
{
ios::sync_with_stdio(false);
cin >> n >> m >> t;
memset(dp,-1,sizeof(dp));
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
char c;
cin >> c;
if(c == '*'){
mp[i][j] = 0;
}
if(c == '.'){
mp[i][j] = 1;
}
}
}
cin >>y_begin>>x_begin>>y_end>>x_end;
int s = t;
cout << dfs(x_begin,y_begin,s);
return 0;
}
3、[SHOI2002]滑雪
题目描述
Michael 喜欢滑雪。这并不奇怪,因为滑雪的确很刺激。可是为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待升降机来载你。Michael 想知道在一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子:
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一,当且仅当高度会减小。在上面的例子中,一条可行的滑坡为 24-17-16-1(从 24 开始,在 1 结束)。当然 25-24-23-…-3-2-1 更长。事实上,这是最长的一条。
输入格式
输入的第一行为表示区域的二维数组的行数 R 和列数 C。下面是 R 行,每行有 C 个数,代表高度(两个数字之间用 1 个空格间隔)。
输出格式
输出区域中最长滑坡的长度。
输入输出样例
输入 #1
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
输出 #1
25
说明/提示
对于 100% 的数据,1≤R,C≤100。
有了上一道题的铺垫,这道题就简单很多了,而且因为这道题对高度的限制使每个点的移动都是单向的,这简化了操作过程,因为我们只需要把每个点都求一遍即可,如果在计算过程中恰好算出了其他点,就可以直接利用(比如我们一开始恰好选到了样例里的25,那其他点就都不需要再算了,直接return即可),这里记忆的主要是每个点的情况
AC code
#include <bits/stdc++.h>
#pragma GCC optimize(3,"Ofast","inline")
#define re register
#define ll long long
#define ull unsigned long long
#define r read()
using namespace std;
//速读
inline int read()
{
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)){
if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)){
x=x*10+ch-48;ch=getchar();}
return x*f;
}
//并查集
int f[1];
int found(int k){
if(f[k] == k){
return k;
}
return f[k] = found(f[k]);
}
//辗转相除法
int gcd(int p,int q){
int t = p % q;
return t==0?q:gcd(q,t);
}
//阶乘
int fac(int k){
int ans = 1;
for(int i = 1; i<= k; i++){
ans *= i;
}
return ans;
}
int mp[105][105];
int dp[105][105];
int m,n;
int dfs(int x,int y){
if(dp[y][x] != -1){
return dp[y][x];
}
if(x == 0 || x == m + 1 || y == 0 || y == n + 1){
return 0;
}
int ans = 0;
if(mp[y][x] > mp[y][x+1]){
ans = max(ans,dfs(x+1,y));
}
if(mp[y][x] > mp[y][x-1]){
ans = max(ans,dfs(x-1,y));
}
if(mp[y][x] > mp[y-1][x]){
ans = max(ans,dfs(x,y-1));
}
if(mp[y][x] > mp[y+1][x]){
ans = max(ans,dfs(x,y+1));
}
return dp[y][x] = ans + 1;
}
int main()
{
ios::sync_with_stdio(false);
n = r;
m = r;
memset(dp,-1,sizeof(dp));
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
mp[i][j] = r;
}
}
int res = 0;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
res = max(res,dfs(j,i));
}
}
cout<<res<<endl;
return 0;
}