图像分类2

一、优化算法

优化遇到的挑战

局部最优


鞍点与海森矩阵(Hessian Matric)

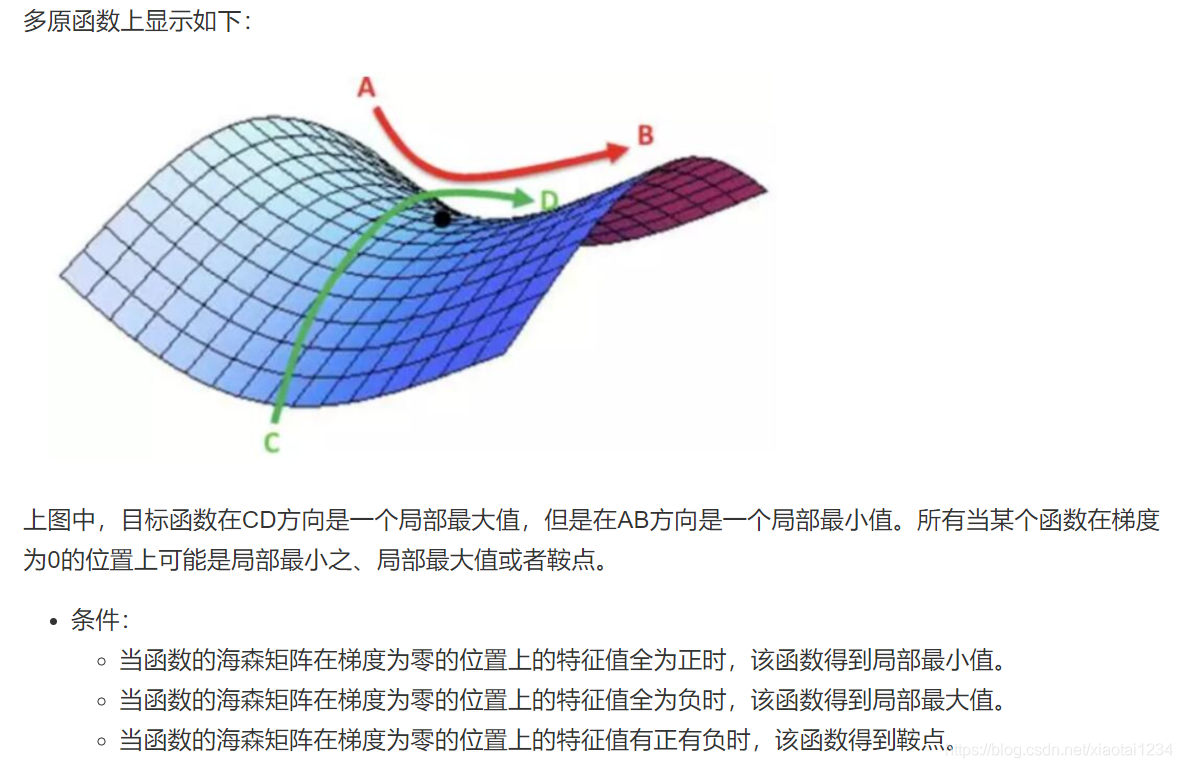



梯度消失


2.批梯度下降算法(Batch Gradient Descent)

Mini-Batch Gradient Descent

批梯度下降与Mini-Batch梯度下降的区别

梯度下降优化影响

大小选择

3.优化算法

动量梯度下降(Gradient Descent with Momentum)





逐参数适应学习率方法






4.学习率退火

5.参数初始化策略与归一化输入
参数初始化

归一化输入



6.案例:动量梯度下降与Adam优化算法实现


momentum算法实现
def initialize_momentum(parameters):
"""
初始化网络中每一层的动量梯度下降的指数加权平均结果参数
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
return:
v['dW' + str(l)] = velocity of dWl
v['db' + str(l)] = velocity of dbl
"""
# 得到网络的层数
L = len(parameters) // 2
v = {
}
# 初始化动量参数
for l in range(L):
v["dW" + str(l + 1)] = np.zeros(parameters['W' + str(l + 1)].shape)
v["db" + str(l + 1)] = np.zeros(parameters['b' + str(l + 1)].shape)
return v
def update_parameters_with_momentum(parameters, gradients, v, beta, learning_rate):
"""
动量梯度下降算法实现
"""
# 得到网络的层数
L = len(parameters) // 2
# 动量梯度参数更新
for l in range(L):
v["dW" + str(l + 1)] = beta * v["dW" + str(l + 1)] + (1 - beta) * (gradients["dW" + str(l + 1)])
v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] + (1 - beta) * (gradients["db" + str(l + 1)])
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * v["dW" + str(l + 1)]
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * v["db" + str(l + 1)]
return parameters, v
adam算法实现
def initialize_adam(parameters):
"""
初始化Adam算法中的参数
"""
# 得到网络的参数
L = len(parameters) // 2
v = {
}
s = {
}
# 利用输入,初始化参数v,s
for l in range(L):
v["dW" + str(l + 1)] = np.zeros(parameters['W' + str(l + 1)].shape)
v["db" + str(l + 1)] = np.zeros(parameters['b' + str(l + 1)].shape)
s["dW" + str(l + 1)] = np.zeros(parameters['W' + str(l + 1)].shape)
s["db" + str(l + 1)] = np.zeros(parameters['b' + str(l + 1)].shape)
return v, s
def update_parameters_with_adam(parameters, gradients, v, s, t, learning_rate=0.01,
beta1=0.9, beta2=0.999, epsilon=1e-8):
"""
更新Adam算法网络的参数
"""
# 网络大小
L = len(parameters) // 2
v_corrected = {
}
s_corrected = {
}
# 更新所有参数
for l in range(L):
# 对梯度进行移动平均计算. 输入: "v, gradients, beta1". 输出: "v".
# 进行动量那部分的计算
v["dW" + str(l + 1)] = beta1 * v["dW" + str(l + 1)] + (1 - beta1) * gradients["dW" + str(l + 1)]
v["db" + str(l + 1)] = beta1 * v["db" + str(l + 1)] + (1 - beta1) * gradients["db" + str(l + 1)]
# 计算修正结果. 输入: "v, beta1, t". 输出: "v_corrected".
v_corrected["dW" + str(l + 1)] = v["dW" + str(l + 1)] / (1 - np.power(beta1, t))
v_corrected["db" + str(l + 1)] = v["db" + str(l + 1)] / (1 - np.power(beta1, t))
# 平方梯度的移动平均值. 输入: "s, gradients, beta2". 输出: "s".
s["dW" + str(l + 1)] = beta2 * s["dW" + str(l + 1)] + (1 - beta2) * np.power(gradients["dW" + str(l + 1)], 2)
s["db" + str(l + 1)] = beta2 * s["db" + str(l + 1)] + (1 - beta2) * np.power(gradients["db" + str(l + 1)], 2)
# 计算修正的结果. 输入: "s, beta2, t". 输出: "s_corrected".
s_corrected["dW" + str(l + 1)] = s["dW" + str(l + 1)] / (1 - np.power(beta2, t))
s_corrected["db" + str(l + 1)] = s["db" + str(l + 1)] / (1 - np.power(beta2, t))
# 更新参数. 输入: "parameters, learning_rate, v_corrected, s_corrected, epsilon". 输出: "parameters".
parameters['W' + str(l + 1)] = parameters['W' + str(l + 1)] - learning_rate * v_corrected[
"dW" + str(l + 1)] / np.sqrt(s_corrected["dW" + str(l + 1)] + epsilon)
parameters['b' + str(l + 1)] = parameters['b' + str(l + 1)] - learning_rate * v_corrected[
"db" + str(l + 1)] / np.sqrt(s_corrected["db" + str(l + 1)] + epsilon)
return parameters, v, s
运行效果如下
# adam算法优化效果
第 0 次迭代的损失值: 0.690552
第 1000 次迭代的损失值: 0.185501
第 2000 次迭代的损失值: 0.150830
第 3000 次迭代的损失值: 0.074454
第 4000 次迭代的损失值: 0.125959
第 5000 次迭代的损失值: 0.104344
第 6000 次迭代的损失值: 0.100676
第 7000 次迭代的损失值: 0.031652
第 8000 次迭代的损失值: 0.111973
第 9000 次迭代的损失值: 0.197940
Accuracy: 0.94
# momentum算法优化效果
第 0 次迭代的损失值: 0.690741
第 1000 次迭代的损失值: 0.685341
第 2000 次迭代的损失值: 0.647145
第 3000 次迭代的损失值: 0.619594
第 4000 次迭代的损失值: 0.576665
第 5000 次迭代的损失值: 0.607324
第 6000 次迭代的损失值: 0.529476
第 7000 次迭代的损失值: 0.460936
第 8000 次迭代的损失值: 0.465780
第 9000 次迭代的损失值: 0.464740
Accuracy: 0.7966666666666666
二、深度学习正则化
1.偏差与方差
数据集划分

偏差与方差的意义

解决方法

2.正则化(Regularization)
正则化,即在成本函数中加入一个正则化项(惩罚项),惩罚模型的复杂度,防止网络过拟合
L1与L2正则化(复习)

正则化项的理解

神经网络中的正则化

L1与L2正则化为什么能够防止过拟合

3.Droupout正则化

1、过拟合是一个严重的问题。大型网络的使用速度也较慢,这使得在测试时结合许多不同的大型神经网络的预测来处理过拟合问题变得非常棘手。Dropout是解决这个问题的一种技巧。关键的想法是在训练过程中,从神经网络中随机丢弃神经元(以及它们的连接)
2、在训练过程中,dropout技巧会从指数级的的不同的“稀疏”网络中抽取样本。在测试时,就可以很容易地估计出所有这些稀疏网络的预测结果的平均。这显著地减少了过拟合,并且比其他正则化方法有了很大的改进
3、drop改进了神经网络在视觉、语音识别、文档分类和计算生物学等监督学习任务上的性能,获得了许多基准数据集state-of-the-art结果。


Dropout 模型描述









Droupout为什么有效(如何理解)

Dropout实用指南

4.案例:DropOut机制与L2正则化实现


def forward_propagation_with_dropout(X, parameters, keep_prob=0.5):
"""
带有dropout的前向传播
"""
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
# 计算第一层输出,对余下的非0的进行扩大倍数,因为p<0。0/x=0,所以0不影响
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
D1 = np.random.binomial(n=1, p=keep_prob, size=A1.shape)
A1 = np.multiply(A1, D1)
A1 /= keep_prob
# 计算第二层输出
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
D2 = np.random.binomial(n=1, p=keep_prob, size=A2.shape)
A2 = np.multiply(A2, D2)
A2 /= keep_prob
# 最后一层输出
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cache
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
"""
droupout的反向传播
需要随机失活神经元,同样对输出做扩大
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1. / m * np.dot(dZ3, A2.T)
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dA2 = np.multiply(dA2, D2)
dA2 /= keep_prob
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1. / m * np.dot(dZ2, A1.T)
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dA1 = np.multiply(dA1, D1)
dA1 /= keep_prob
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * np.dot(dZ1, X.T)
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {
"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients

# -------
# 1、有正则化的损失函数计算
# 2、正则化后的反向传播计算
# -------
def compute_cost_with_regularization(A3, Y, parameters, lambd):
"""
损失函数中增加L2正则化
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
# 1、计算交叉熵损失
cross_entropy_cost = compute_cost(A3, Y)
# 2、加入L2正则化的损失部分
L2_regularization_cost = (1. / m) * (lambd / 2) * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3)))
# 两个损失进行合并,完整损失
cost = cross_entropy_cost + L2_regularization_cost
return cost
def backward_propagation_with_regularization(X, Y, cache, lambd):
"""
对增加了L2正则化后的损失函数进行反向传播计算
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
# 含有正则化的反向传播公式
# z = a - y
# # dw = 1/ m * ((dz*A.T)+ lambd * w)
dZ3 = A3 - Y
dW3 = 1. / m * (np.dot(dZ3, A2.T) + lambd * W3)
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1. / m * (np.dot(dZ2, A1.T) + lambd * W2)
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * (np.dot(dZ1, X.T) + lambd * W1)
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {
"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
运行效果
# dropout
迭代次数为 0: 损失结果大小:0.6616994233431039
迭代次数为 10000: 损失结果大小:0.20018054682333422
迭代次数为 20000: 损失结果大小:0.197457875306683
训练集的准确率:
Accuracy: 0.9383886255924171
测试集的准确率:
Accuracy: 0.95
# 正则化
迭代次数为 0: 损失结果大小:0.6543912405149825
迭代次数为 10000: 损失结果大小:0.0
迭代次数为 20000: 损失结果大小:0.0
训练集的准确率:
Accuracy: 0.9289099526066351
测试集的准确率:
Accuracy: 0.95
5.神经网络调优

调参技巧

运行

6.批标准化(Batch Normalization)



批标准化公式

过程图

为什么批标准化能够是优化过程变得简单

BN总结

7.其它方法

早停止法(Early Stopping)

数据增强



数据增强技术


从左侧开始分别为:原始图像,从左上角裁剪出一个正方形部分,然后从右下角裁剪出一个正方形部分。剪裁的部分被调整为原始图像大小。



效果
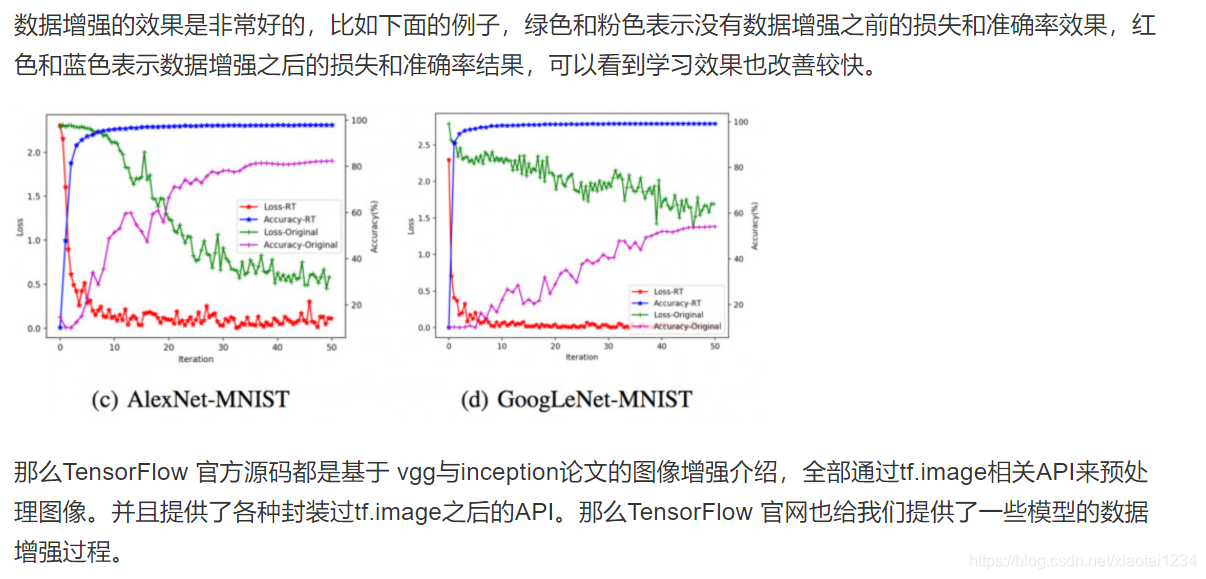
数据增强库

三、卷积神经网络(CNN)
1.为什么需要卷积神经网络

图像特征数量对神经网络效果压力


2.感受野的来源

3.边缘检测


4.卷积神经网络的组成

卷积层

卷积运算过程


padding-零填充

Valid and Same卷积

奇数维度的过滤器

stride-步长

多通道卷积

多卷积核

5.卷积总结

设计单个卷积Filter的计算公式

卷积层实现代码介绍
以下代码主要通过numpy进行实现,再此我们只介绍实现过程理解,并不需要大家手写这样的代码,帮助理解原理过程。卷积实现的难点在于如何通过图片和过滤器去循环图片获得区域。
def conv_(img, conv_filter):
"""
卷积核计算操作
:param img: 图片数据
:param conv_filter: 卷积核
:return:
"""
# 1、获取卷积核的大小
filter_size = conv_filter.shape[1]
# 初始化卷积后的结果,给个较大的输出结果
result = np.zeros((img.shape))
# 2、对图片进行循环使用卷积操作(获取当前区域并使用过滤器进行相乘操作.)
# (1)r和c为特征图的下表,从0到特征图输出大小
for r in np.uint16(np.arange(filter_size/2.0, img.shape[0]-filter_size/2.0+1)):
for c in np.uint16(np.arange(filter_size/2.0, img.shape[1]-filter_size/2.0+1)):
# 取出过滤器大小的图片区域,从图片左上角开始
curr_region = img[r-np.uint16(np.floor(filter_size/2.0)):r+np.uint16(np.ceil(filter_size/2.0)),
c-np.uint16(np.floor(filter_size/2.0)):c+np.uint16(np.ceil(filter_size/2.0))]
# 图片当前区域与卷积核进行线性相乘
curr_result = curr_region * conv_filter
# 结果求和并保存,按照下表保存
conv_sum = np.sum(curr_result)
result[r, c] = conv_sum
# 裁剪矩阵
final_result = result[np.uint16(filter_size/2.0):result.shape[0]-np.uint16(filter_size/2.0),
np.uint16(filter_size/2.0):result.shape[1]-np.uint16(filter_size/2.0)]
return final_result
def conv(img, conv_filter):
"""
卷积过程实现
:param img: 图像
:param conv_filter: 卷积过滤器
:return:
"""
# 1、输入的参数大小做异常检测
# 检查输入的图片和卷积核是否一样大小
if len(img.shape) != len(conv_filter.shape) - 1:
print("Error: Number of dimensions in conv filter and image do not match.")
exit()
# 检查输入的图片的通道数和卷积的深度一样
if len(img.shape) > 2 or len(conv_filter.shape) > 3:
if img.shape[-1] != conv_filter.shape[-1]:
print("Error: Number of channels in both image and filter must match.")
sys.exit()
# 检查是否过滤器的长宽一样
if conv_filter.shape[1] != conv_filter.shape[2]:
print('Error: Filter must be a square matrix. I.e. number of rows and columns must match.')
sys.exit()
# 检查过滤器的维度是奇数
if conv_filter.shape[1] % 2 == 0:
print('Error: Filter must have an odd size. I.e. number of rows and columns must be odd.')
sys.exit()
# 2、初始化一个空的特征图来装入计算的结果
feature_maps = np.zeros((img.shape[0]-conv_filter.shape[1]+1,
img.shape[1]-conv_filter.shape[1]+1,
conv_filter.shape[0]))
# 3、图片的卷积完整操作(分别使用每一个过滤器进行过滤操作)
for filter_num in range(conv_filter.shape[0]):
print("Filter ", filter_num + 1)
# 获取当前的filter参数
curr_filter = conv_filter[filter_num, :]
# 当前filter进行卷积核计算操作
if len(curr_filter.shape) > 2:
# 对图片的每个channel进行卷积运算
conv_map = conv_(img[:, :, 0], curr_filter[:, :, 0])
for ch_num in range(1, curr_filter.shape[-1]):
conv_map = conv_map + conv_(img[:, :, ch_num], curr_filter[:, :, ch_num])
else:
# 只有一个filter的情况
conv_map = conv_(img, curr_filter)
feature_maps[:, :, filter_num] = conv_map
return feature_maps
# 使用过程
# 1、定义这层有两个卷积核,每个大小3x3(例子默认对黑白图片进行计算),默认一个步长,不零填充
l1_filter = np.zeros((2,3,3))
# 初始化参数
l1_filter[0, :, :] = np.array([[[-1, 0, 1],
[-1, 0, 1],
[-1, 0, 1]]])
l1_filter[1, :, :] = np.array([[[1, 1, 1],
[0, 0, 0],
[-1, -1, -1]]])
# 卷积计算
l1_feature_map = cnn.conv(img, l1_filter)

池化层(Pooling)


最大池化层实现代码解释
def pooling(feature_map, size=2, stride=2):
"""
最大池化实现
:param feature_map: 特征图
:param size: 池化大小
:param stride: 步长
:return:
"""
# 1、准备池化层的输出初始化
pool_out = np.zeros((np.uint16((feature_map.shape[0] - size + 1) / stride + 1),
np.uint16((feature_map.shape[1] - size + 1) / stride + 1),
feature_map.shape[-1]))
# 2、循环取出每个方格当中的最大值作为新的输出
for map_num in range(feature_map.shape[-1]):
# 获取左上角横初始下标
r2 = 0
for r in np.arange(0, feature_map.shape[0] - size + 1, stride):
# 获取左上角纵初始下标
c2 = 0
for c in np.arange(0, feature_map.shape[1] - size + 1, stride):
pool_out[r2, c2, map_num] = np.max([feature_map[r:r + size, c:c + size, map_num]])
c2 = c2 + 1
r2 = r2 + 1
return pool_out
全连接层

案例:通过封装的接口构建一个卷积网络



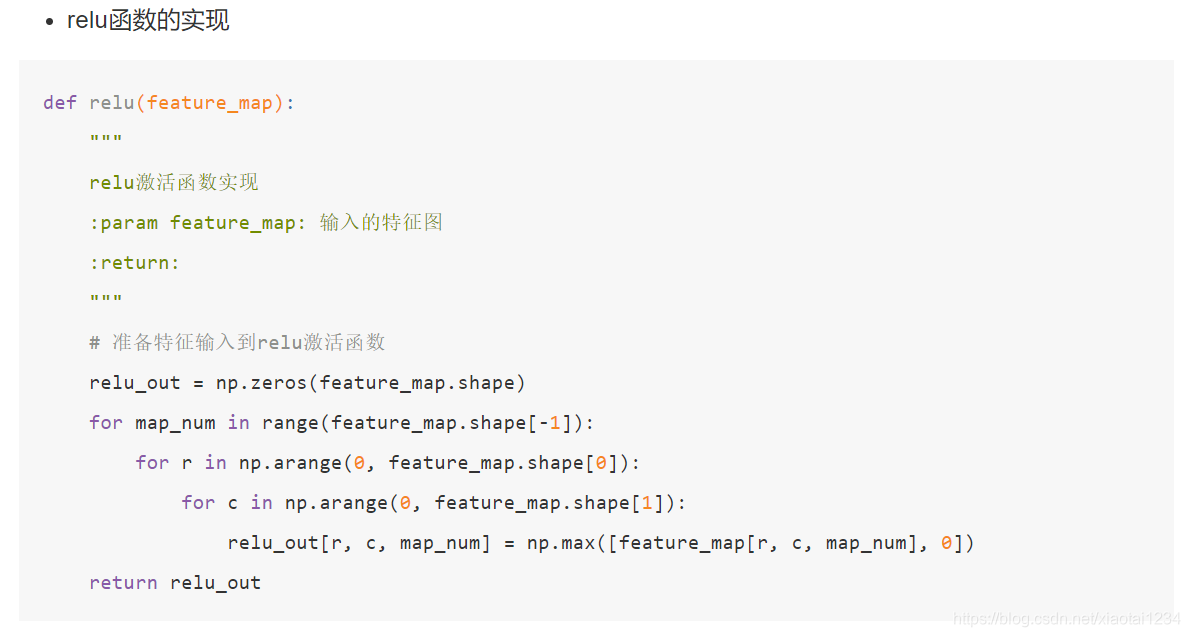
最后的输出显示绘图
# 3、画出输出结果
fig0, ax0 = pyplot.subplots(nrows=1, ncols=1)
ax0.imshow(img).set_cmap("gray")
ax0.set_title("Input Image")
ax0.get_xaxis().set_ticks([])
ax0.get_yaxis().set_ticks([])
pyplot.savefig("in_img.png", bbox_inches="tight")
pyplot.close(fig0)
# 第三层卷积层输出结果显示
fig3, ax3 = pyplot.subplots(nrows=1, ncols=3)
ax3[0].imshow(l3_feature_map[:, :, 0]).set_cmap("gray")
ax3[0].get_xaxis().set_ticks([])
ax3[0].get_yaxis().set_ticks([])
ax3[0].set_title("L3-Map1")
ax3[1].imshow(l3_feature_map_relu[:, :, 0]).set_cmap("gray")
ax3[1].get_xaxis().set_ticks([])
ax3[1].get_yaxis().set_ticks([])
ax3[1].set_title("L3-Map1ReLU")
ax3[2].imshow(l3_feature_map_relu_pool[:, :, 0]).set_cmap("gray")
ax3[2].get_xaxis().set_ticks([])
ax3[2].get_yaxis().set_ticks([])
ax3[2].set_title("L3-Map1ReLUPool")
pyplot.savefig("L3.png", bbox_inches="tight")
pyplot.close(fig3)

6.卷积网络的感受野Receptive field (RF)以及计算
为什么学习感受野

感受野定义


计算

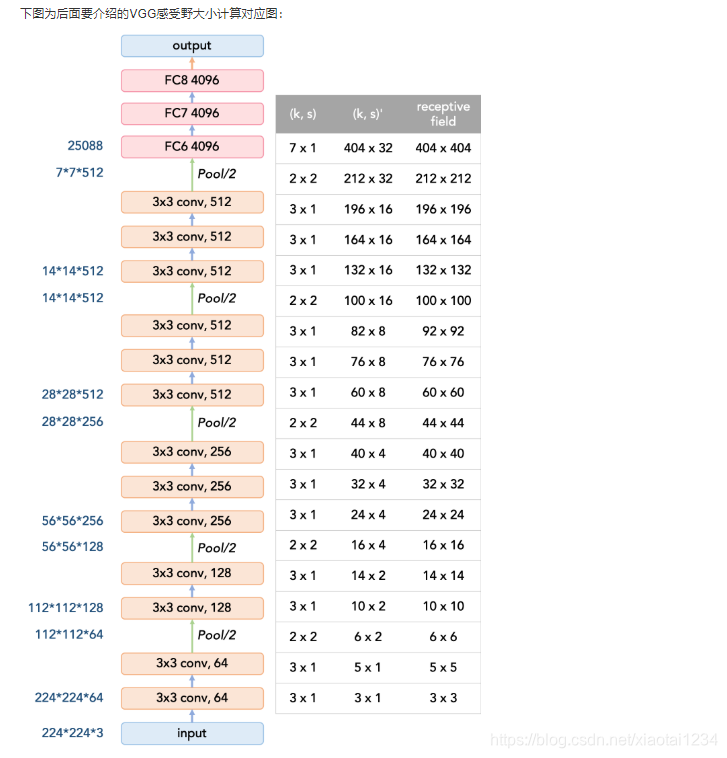
四、CNN架构

1.LeNet-5解析

网络结构

参数形状总结

2.AlexNet

3.卷积网络结构的优化
常见结构特点


4.VGG

def VGG_16():
model = Sequential()
model.add(Conv2D(64,(3,3),strides=(1,1),input_shape=(224,224,3),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(64,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(128,(3,2),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(128,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(256,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(256,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(256,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(4096,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(4096,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1000,activation='softmax'))
return model
5.Inception 结构
首先我们要说一下在Network in Network中引入的1 x 1卷积结构的相关作用,下面我们来看1*1卷积核的优点:
MLP卷积(1 x 1卷积)

1 x 1卷积介绍

通道数变化


Inception层

Inception v1-Pointwise Conv



GoogleNet结构


def Conv2d_BN(x, nb_filter,kernel_size, padding='same',strides=(1,1),name=None):
if name is not None:
bn_name = name + '_bn'
conv_name = name + '_conv'
else:
bn_name = None
conv_name = None
x = Conv2D(nb_filter,kernel_size,padding=padding,strides=strides,activation='relu',name=conv_name)(x)
x = BatchNormalization(axis=3,name=bn_name)(x)
return x
def Inception(x,nb_filter):
branch1x1 = Conv2d_BN(x,nb_filter,(1,1), padding='same',strides=(1,1),name=None)
branch3x3 = Conv2d_BN(x,nb_filter,(1,1), padding='same',strides=(1,1),name=None)
branch3x3 = Conv2d_BN(branch3x3,nb_filter,(3,3), padding='same',strides=(1,1),name=None)
branch5x5 = Conv2d_BN(x,nb_filter,(1,1), padding='same',strides=(1,1),name=None)
branch5x5 = Conv2d_BN(branch5x5,nb_filter,(1,1), padding='same',strides=(1,1),name=None)
branchpool = MaxPooling2D(pool_size=(3,3),strides=(1,1),padding='same')(x)
branchpool = Conv2d_BN(branchpool,nb_filter,(1,1),padding='same',strides=(1,1),name=None)
x = concatenate([branch1x1,branch3x3,branch5x5,branchpool],axis=3)
return x
def GoogLeNet():
inpt = Input(shape=(224,224,3))
#padding = 'same',填充为(步长-1)/2,还可以用ZeroPadding2D((3,3))
x = Conv2d_BN(inpt,64,(7,7),strides=(2,2),padding='same')
x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding='same')(x)
x = Conv2d_BN(x,192,(3,3),strides=(1,1),padding='same')
x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding='same')(x)
x = Inception(x,64)#256
x = Inception(x,120)#480
x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding='same')(x)
x = Inception(x,128)#512
x = Inception(x,128)
x = Inception(x,128)
x = Inception(x,132)#528
x = Inception(x,208)#832
x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding='same')(x)
x = Inception(x,208)
x = Inception(x,256)#1024
x = AveragePooling2D(pool_size=(7,7),strides=(7,7),padding='same')(x)
x = Dropout(0.4)(x)
x = Dense(1000,activation='relu')(x)
x = Dense(1000,activation='softmax')(x)
model = Model(inpt,x,name='inception')
return model
Inception v2

Inception v3


Inception v4

Xception - Depthwise Separable Conv(深度可分离卷积)





Inception Module 总结

6.ResNet-里程碑式创新


残差网络-Residual network








实验

完整结构

代码实现
def Conv2D_BN(x, filters, kernel_size, strides=(1, 1), padding='same', name=None):
if name:
bn_name = name + '_bn'
conv_name = name + '_conv'
else:
bn_name = None
conv_name = None
x = Conv2D(filters, kernel_size, strides=strides, padding=padding, activation='relu', name=conv_name)(x)
x = BatchNormalization(name=bn_name)(x)
return x
def identity_block(input_tensor, filters, kernel_size, strides=(1, 1), is_conv_shortcuts=False):
"""
:param input_tensor:
:param filters:
:param kernel_size:
:param strides:
:param is_conv_shortcuts: 直接连接或者投影连接
:return:
"""
x = Conv2D_BN(input_tensor, filters, kernel_size, strides=strides, padding='same')
x = Conv2D_BN(x, filters, kernel_size, padding='same')
if is_conv_shortcuts:
shortcut = Conv2D_BN(input_tensor, filters, kernel_size, strides=strides, padding='same')
x = add([x, shortcut])
else:
x = add([x, input_tensor])
return x
def bottleneck_block(input_tensor, filters=(64, 64, 256), strides=(1, 1), is_conv_shortcuts=False):
"""
:param input_tensor:
:param filters:
:param strides:
:param is_conv_shortcuts: 直接连接或者投影连接
:return:
"""
filters_1, filters_2, filters_3 = filters
x = Conv2D_BN(input_tensor, filters=filters_1, kernel_size=(1, 1), strides=strides, padding='same')
x = Conv2D_BN(x, filters=filters_2, kernel_size=(3, 3))
x = Conv2D_BN(x, filters=filters_3, kernel_size=(1, 1))
if is_conv_shortcuts:
short_cut = Conv2D_BN(input_tensor, filters=filters_3, kernel_size=(1, 1), strides=strides)
x = add([x, short_cut])
else:
x = add([x, input_tensor])
return x
def ResNet34(input_shape=(224, 224, 3), n_classes=1000):
"""
:param input_shape:
:param n_classes:
:return:
"""
input_layer = Input(shape=input_shape)
x = ZeroPadding2D((3, 3))(input_layer)
# block1
x = Conv2D_BN(x, filters=64, kernel_size=(7, 7), strides=(2, 2), padding='valid')
x = MaxPooling2D(pool_size=(3, 3), strides=2, padding='same')(x)
# block2
x = identity_block(x, filters=64, kernel_size=(3, 3))
x = identity_block(x, filters=64, kernel_size=(3, 3))
x = identity_block(x, filters=64, kernel_size=(3, 3))
# block3
x = identity_block(x, filters=128, kernel_size=(3, 3), strides=(2, 2), is_conv_shortcuts=True)
x = identity_block(x, filters=128, kernel_size=(3, 3))
x = identity_block(x, filters=128, kernel_size=(3, 3))
x = identity_block(x, filters=128, kernel_size=(3, 3))
# block4
x = identity_block(x, filters=256, kernel_size=(3, 3), strides=(2, 2), is_conv_shortcuts=True)
x = identity_block(x, filters=256, kernel_size=(3, 3))
x = identity_block(x, filters=256, kernel_size=(3, 3))
x = identity_block(x, filters=256, kernel_size=(3, 3))
x = identity_block(x, filters=256, kernel_size=(3, 3))
x = identity_block(x, filters=256, kernel_size=(3, 3))
# block5
x = identity_block(x, filters=512, kernel_size=(3, 3), strides=(2, 2), is_conv_shortcuts=True)
x = identity_block(x, filters=512, kernel_size=(3, 3))
x = identity_block(x, filters=512, kernel_size=(3, 3))
x = AveragePooling2D(pool_size=(7, 7))(x)
x = Flatten()(x)
x = Dense(n_classes, activation='softmax')(x)
model = Model(inputs=input_layer, outputs=x)
return model
def ResNet50(input_shape=(224, 224, 3), n_classes=1000):
"""
:param input_shape:
:param n_classes:
:return:
"""
input_layer = Input(shape=input_shape)
x = ZeroPadding2D((3, 3))(input_layer)
# block1
x = Conv2D_BN(x, filters=64, kernel_size=(7, 7), strides=(2, 2), padding='valid')
x = MaxPooling2D(pool_size=(3, 3), strides=(2, 2), padding='same')(x)
# block2
x = bottleneck_block(x, filters=(64, 64, 256), strides=(1, 1), is_conv_shortcuts=True)
x = bottleneck_block(x, filters=(64, 64, 256))
x = bottleneck_block(x, filters=(64, 64, 256))
# block3
x = bottleneck_block(x, filters=(128, 128, 512), strides=(2, 2), is_conv_shortcuts=True)
x = bottleneck_block(x, filters=(128, 128, 512))
x = bottleneck_block(x, filters=(128, 128, 512))
x = bottleneck_block(x, filters=(128, 128, 512))
# block4
x = bottleneck_block(x, filters=(256, 256, 1024), strides=(2, 2), is_conv_shortcuts=True)
x = bottleneck_block(x, filters=(256, 256, 1024))
x = bottleneck_block(x, filters=(256, 256, 1024))
x = bottleneck_block(x, filters=(256, 256, 1024))
x = bottleneck_block(x, filters=(256, 256, 1024))
x = bottleneck_block(x, filters=(256, 256, 1024))
# block5
x = bottleneck_block(x, filters=(512, 512, 2048), strides=(2, 2), is_conv_shortcuts=True)
x = bottleneck_block(x, filters=(512, 512, 2048))
x = bottleneck_block(x, filters=(512, 512, 2048))
x = AveragePooling2D(pool_size=(7, 7))(x)
x = Flatten()(x)
x = Dense(n_classes, activation='softmax')(x)
model = Model(inputs=input_layer, outputs=x)
return model
7.DenseNet-密集连接卷积网络

设计理念


网络结构


DenseNet优点

对比

8.卷积神经网络学习特征可视化



