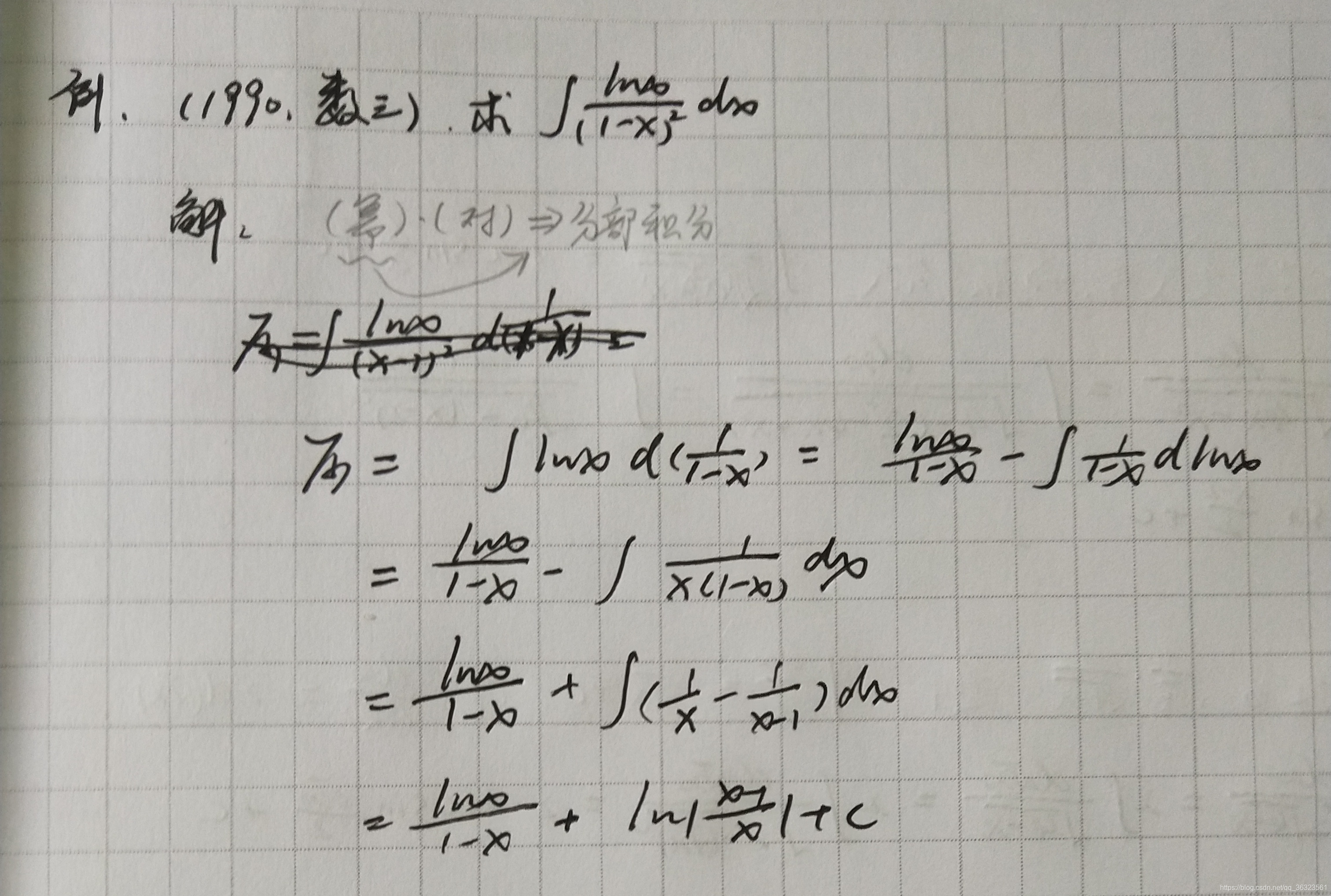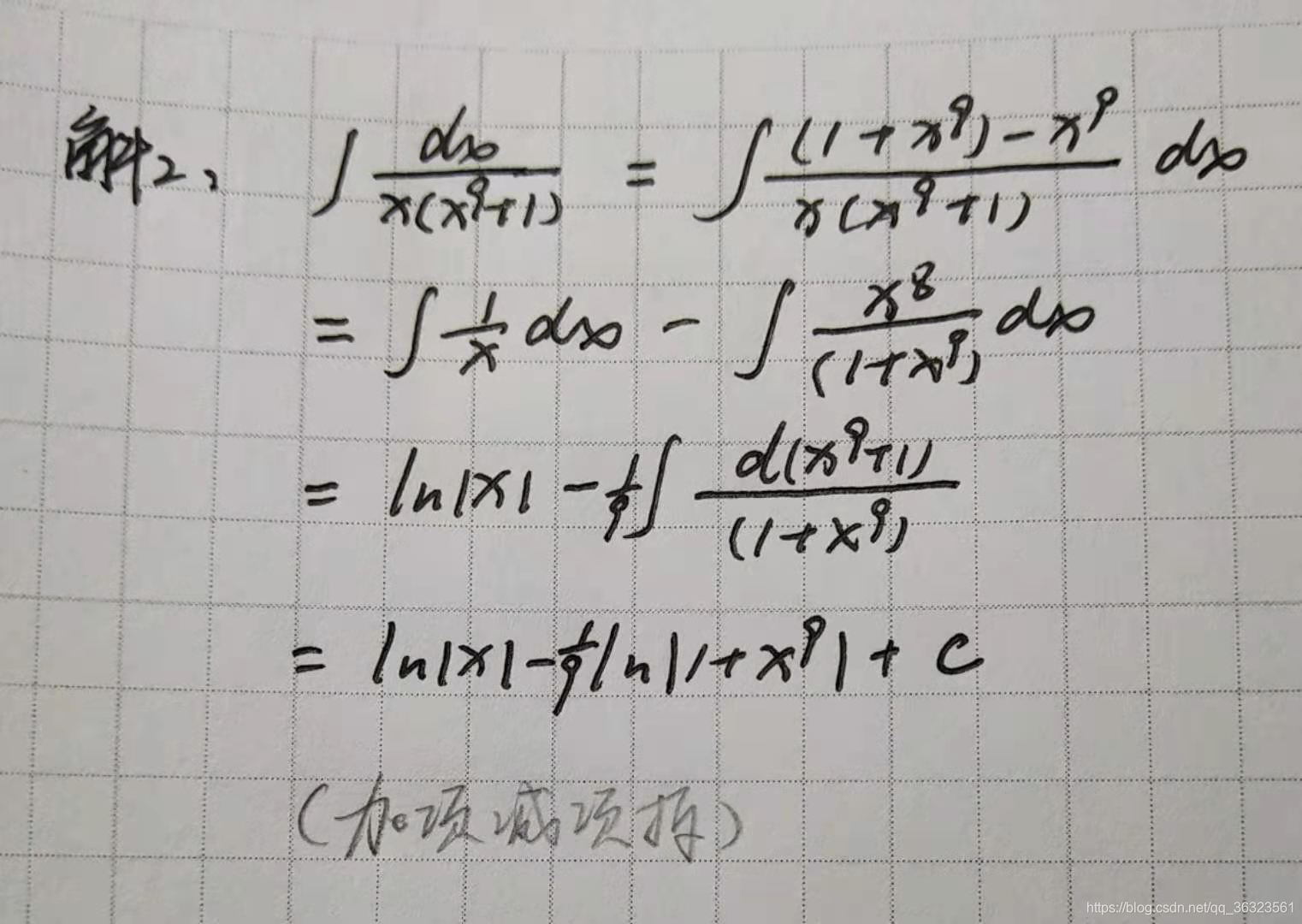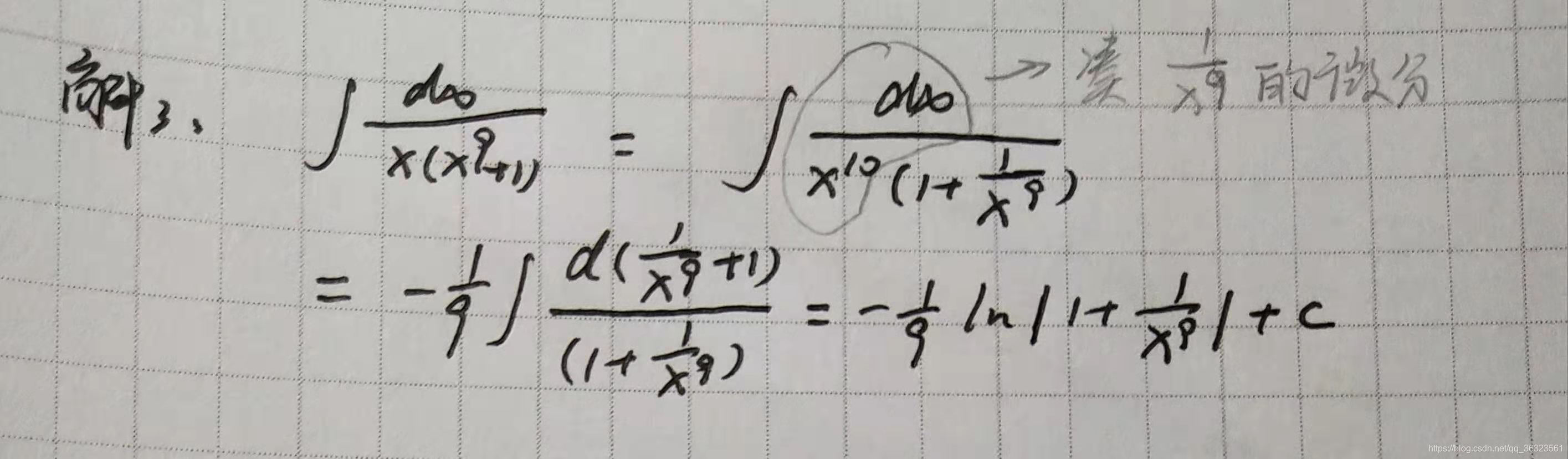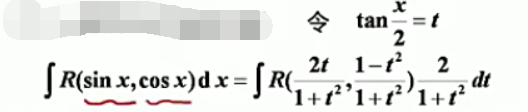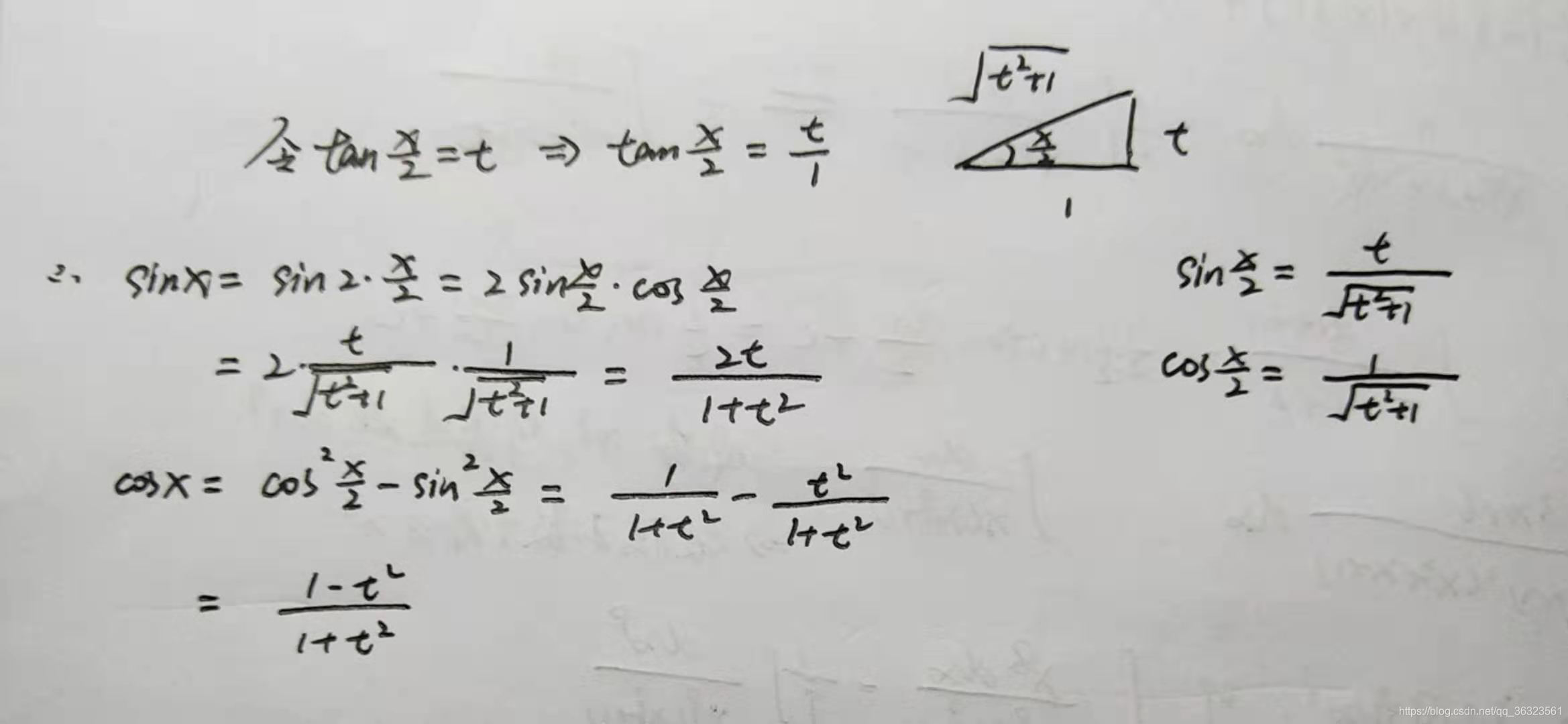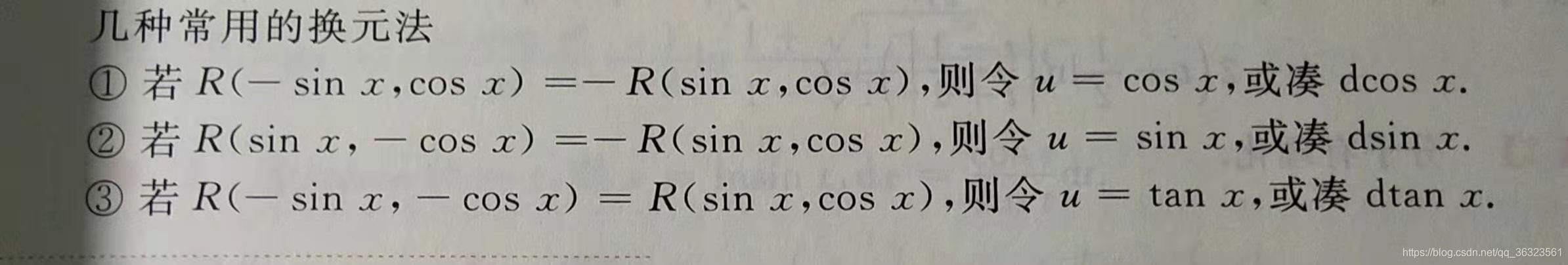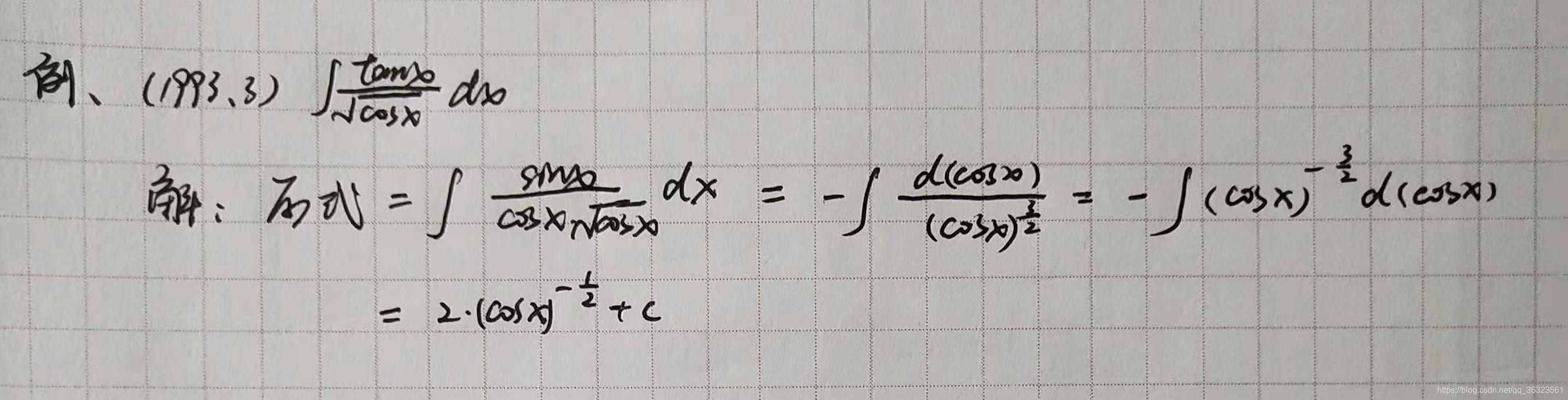一、不定积分的概念与性质
(一)原函数
(二)不定积分
不定积分是 f ( x ) f(x) f(x) 原函数的全体,即一定要加 C C C;
即 f ( x ) f(x) f(x) 所有原函数的函数集合
(三)不定积分的几何意义
- 从几何上看,不定积分是原函数的一簇积分曲线,这些曲线两两相差一个常数 C C C
(四)原函数存在定理
- 并不是所有函数都有原函数
【定理一】
若 f ( x ) f(x) f(x) 在区间 I I I 上连续,则 f ( x ) f(x) f(x) 在区间 I I I 上一定存在原函数
至少f(x)的变上限积分就是f(x)的一个原函数
∫ f ( x ) d x = ∫ a x f ( t ) d t + C \int{f(x)dx}=\int_a^xf(t)dt+C ∫f(x)dx=∫axf(t)dt+C
- 不定积分是 f ( x ) f(x) f(x) 的所有原函数
- 变上限积分是 f ( x ) f(x) f(x) 连续时的一个具体原函数
即 f ( x ) f(x) f(x) 的不定积分为其任意一个具体原函数 + C C C
【定理二】
若 f ( x ) f(x) f(x) 在区间 I I I 上有第一类间断点,则 f ( x ) f(x) f(x) 在区间 I I I 上没有原函数
- 连续函数一定有原函数,但是有原函数的函数不一定连续
- 又因为有第一类间断点的函数一定无原函数,所有有原函数的含间断点的函数只能值含第二类间断点的函数
(五)不定积分的性质
二、不定积分的基本公式

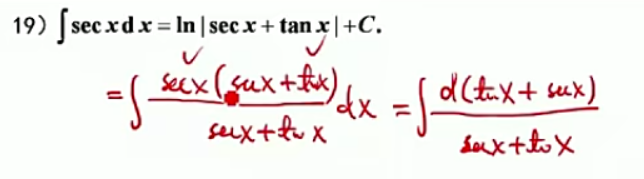
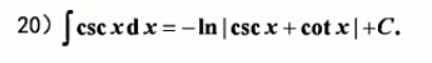
基本积分表的扩展:
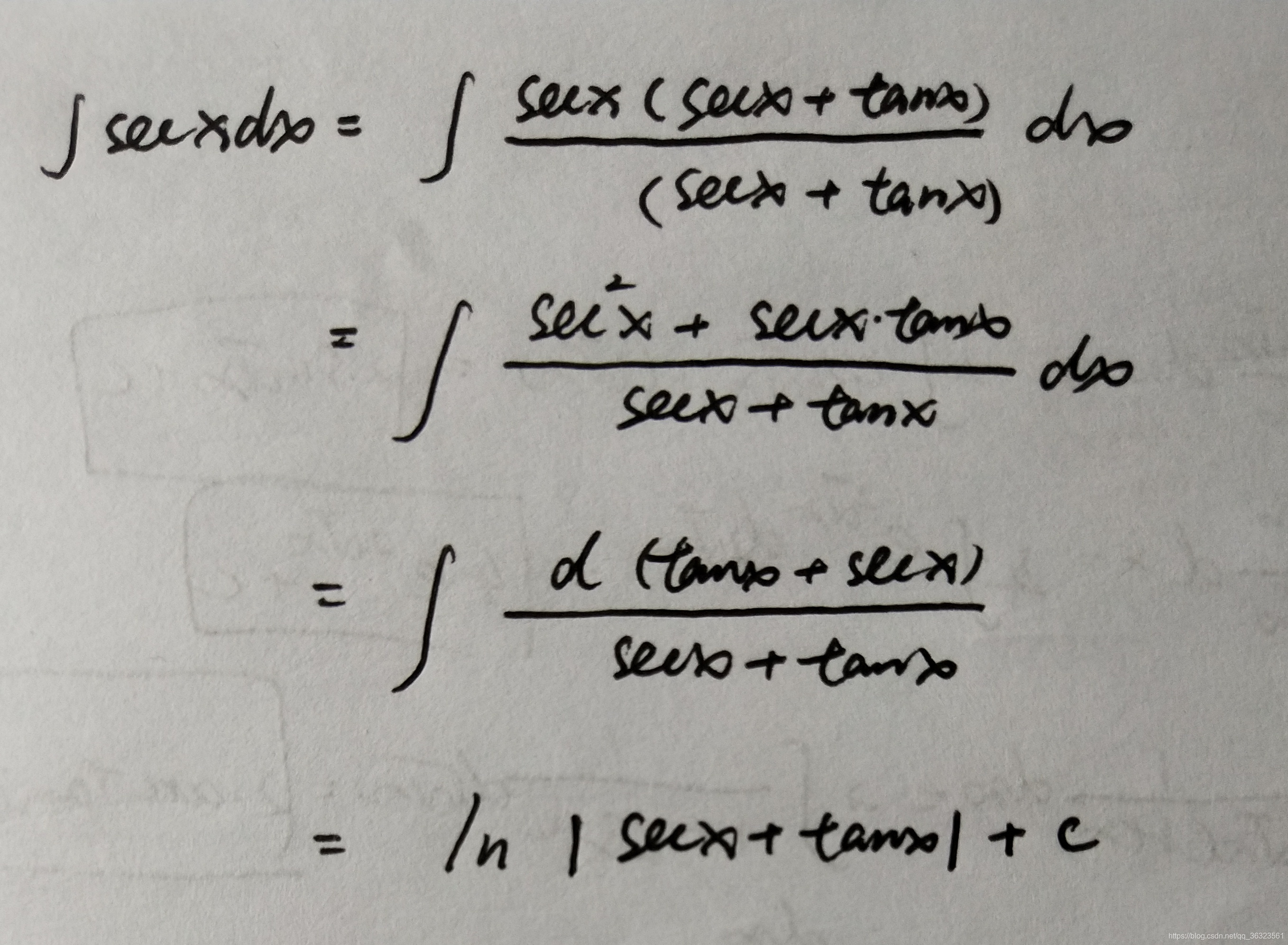
| ∫ sec x d x = ln ∥ sec x + tan x ∥ + C {\int{\sec x}dx}={ {\ln { \| \sec x+\tan x\|}}+{C}} ∫secxdx=ln∥secx+tanx∥+C | 证明 | |
| ∫ csc x d x = − ln ∥ csc x + cot x ∥ + C {\int{\csc x}dx}={ {-\ln { \| \csc x+\cot x\|}}+{C}} ∫cscxdx=−ln∥cscx+cotx∥+C | 证明 | |
| ∫ a 2 − x 2 d x = a 2 2 a r c s i n x a + x 2 a 2 − x 2 + C \int{\sqrt{a^2-x^2}}dx=\frac{a^2}{2}arcsin{\frac{x}{a}}+{\frac{x}{2}\sqrt{a^2-x^2}}+{C} ∫a2−x2dx=2a2arcsinax+2xa2−x2+C |
三、三种主要积分法
“2+1”(2种换元法+1种分部积分法)
前面所学的求导法则中有两条最核心的法则:
① 有理运算:包括:加、减、乘、除
② 复合函数求导法则
将其倒过来应用在积分中
所以积分的主要方法就是将求导数的主要方法倒过来即可
不定积分结果的形式不唯一,求导验证
- 导数的和差运算法则倒过来:得出拆项积分法(积分的和差等于和差的积分)
- 导数的乘法运算法则倒过来:得出分部积分法
- 除法法则倒过来太难用,用得少
- 复合函数倒过来就是两类换元积分法
(一)第一换元积分法(凑微分法)
(二)第二换元积分法(真·换元法)
第二类换元积分法是真正地替换了变量,后面需要反函数还原回来
关键在于变量代换选谁?
原则只有一个,怎么简单怎么来
【常用三种变量代换】
主要用来处理根式
- 被积函数含有 a 2 − x 2 \sqrt{a^2-x^2} a2−x2 ,令 x = a ⋅ s i n t x=a·sint x=a⋅sint(或 a ⋅ c o s t a·cost a⋅cost)
- 被积函数含有 a 2 + x 2 \sqrt{a^2+x^2} a2+x2 ,令 x = a ⋅ t a n t x=a·tant x=a⋅tant
- 被积函数含有 x 2 − a 2 \sqrt{x^2-a^2} x2−a2 ,令 x = a ⋅ s e c t x=a·sect x=a⋅sect
【两类换元积分法比较】
第一类换元法是凑微分,变量是不用替换的;
第二类换元法是换变量,最后需要把变量还原回来
第一类换元积分法 第二类换元积分法 实质 凑微分 换变量,再还原 评价 简单 麻烦
(三)分部积分法
何时用?如何用?
适用类型:两类不同函数相乘(一般指反、对、幂、三、指)
原则:按照顺序,反、对、幂、三、指,将偏后部分凑到微分号里;
其中三角函数与指数函数共存时,顺序随意,但倾向于将指数函数凑到微分号里面
1、在幂函数与指数函数、三角函数共存时,将非幂函数放在微分号后面比较简单;
2、在幂函数与对数函数、反三角函数共存时,将幂函数放在微分号后面比较简单;
3、在指数函数与三角函数共存时,无论哪个函数放在微分号后面都简单(倾向于将指数函数置后)。该类一般需要多次积分。
故:可归纳为(反、对、幂、三、指)
【例】
注意原函数为对数函数时,需要考虑绝对值
四、三类常见可积函数的积分
上述三大积分法所得结果均为初等函数,然而这三大积分法并不能解决所有积分问题,比如: ∫ e x 2 d x \int{e^{x^2}}dx ∫ex2dx ,虽然有原函数,但是不能用初等函数来表示,数学上将这类积分称为 “积不出的积分”。
这里的“积不出”指的是:存在原函数,但是原函数不是初等函数。
【常见的需要掌握的 “积不出的积分”】:
∫ e x 2 d x \int{e^{x^2}}dx ∫ex2dx
∫ s i n x x d x \int{\frac{sinx}{x}}dx ∫xsinxdx
∫ c o s x x d x \int{\frac{cosx}{x}}dx ∫xcosxdx
对于这些积不出的积分,其目的不是为了计算,
比如在二重积分中,出现这种 “积不出的积分”,目的是为了暗示交换次序重新计算
对于这类原函数不是初等函数的被积函数,其(被积函数)积分无法用初等函数表示,故上述三大积分法不能解决这类问题。而部分可积分的形式如下:
1、有理函数
2、三角有理式函数
3、带有简单无理式的函数
(一)有理函数积分
∫ R ( x ) d x \int{R(x)}dx ∫R(x)dx
被积函数是通过变量 x x x 进行有理运算(加减乘除)得到的
结论:凡是有理函数积分,都可以积出来
1、一般法(部分分式法)
三十多年就考过一次,做两道题知道原理即可
【例】
2、特殊方法(加项减项拆或凑微分降幂)
考频高
【例】
方法一:凑微分降幂
方法二:加项减项拆
同方法一:凑微分
(二)三角有理式积分
∫ R ( s i n x , c o s x ) d x \int{R(sinx,cosx)}dx ∫R(sinx,cosx)dx
这里的 R R R 指的是有理运算(加减乘除)
结论:凡是三角有理式的积分,都可解出
1、一般方法(万能代换)
因为原则上,所有有理函数积分都可以积出结果,故通过万能代换将三角函数积分转换为有理函数积分即可利用有理函数的积分进行计算。
万能代换是在万不得已的情况下才使用的,一般对于三角函数积分,首先考虑使用特殊方法。
2、特殊方法(三角变形、换元、分部)
① s i n sin sin 的正负决定被积函数的正负(说明sin是奇数次),则凑 d c o s dcos dcos
② c o s cos cos 的正负决定被积函数的正负(说明cos是奇数次),则凑 d s i n dsin dsin
③ 都影响则凑 d t a n dtan dtan
【例】
本题可见,万能代换一般适用于次数较低的三角有理积分
【例】
对数的真数部分恒正,故省去绝对值
【例】
(三)简单无理数函数积分
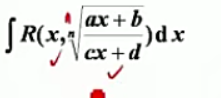
由x和根号经过有理运算所得的函数
- 根号开多少次无所谓
- 关键是根号内部必须是两个一次式之比
结论:这样的积分都可解出;且方法固定,即令根号部分为t。
通过代换可以将这样的无理函数积分替换为可计算的有理函数积分
对于简单无理数函数积分,一般默认只有这种方法。特殊形式很少见
【例】
【例】
【例】
五、总结
思维导图
重点是不定积分的计算方法,换元积分法和分部积分法
要知道,不定积分要多难的题都有,但不比掌握这些难题,考试只考常规题,对于遇到的解不出的题,大多数情况下都有特殊的技巧,然而考研卷子从未考过利用特殊技巧才可解出的不定积分,所以这类题在考研中不会遇到。只要把基本方法练会即可
在尺度方面,不用花时间去练习哪些做不出的题,但是作为基本运算,一定要把常规题练熟
关于和差化积
考研卷子不会出那些非得用和差化积才能做的题目
六、常考题型与典型例题
(一)被积函数为根号
常用第二类换元积分法,将整个被积函数令成 t t t
(二)分母为根号的类型
大致为
∫ A B d x \int{\frac{A}{\sqrt{B}}}dx ∫BAdx
其中, B B B 一般为二次三项式,而 A A A 有两种情况:
① A A A 为零次式,即常数,此时凑反三角函数公式即可
② A A A 为一次式,则需要拆项,凑 A A A 为 B B B 的微分,注意余项应为常数(零次式)
【例】
本题中,B为二次三项式,A为常数,则凑基本公式即可
【例】
本题中,B为二次三项式,A为一次式,则需要用A凑出B的微分,、
此外一定要注意,余下的部分不能仍是一次式,否则前功尽弃;应保证余下的部分为常数(即零次式)
【例】
本例中,B不是二次三项式,该结论不适用于此
实质上,本例为三角函数的熟练运用:
本题见 1 c o s x \frac{1}{\sqrt{cosx}} cosx1 一般想到 d ( c o s x ) d{(cosx}) d(cosx),进而考虑被积函数需要有 s i n x sinx sinx,大致思路如此。
(三)分段函数求不定积分
这种题型考察的不是如何求不定积分;而是考察分段函数在求不定积分的时候,需要注意什么
求不定积分是找原函数,(即所得的结果求导后等于被积函数)一般易错的地方出现在分段点处。
需要保证所得结果在分段点处可导(一般首先看是否连续)
可导性验证比较麻烦,所以起码得在分段点处连续
【思考:为什么在这里保证了连续就能保证可导?】对于这种题型,题干所给的分段函数一般都是连续函数
这里有一个一般理论:(数学上可以证明)
如果被积函数是一个连续函数,那么对其分段做变上限积分,最后调整成任意常数,只要保证做出的结果在分界点处连续,数学上可以证明它一定在那一点可导,且导数值为被积函数在点处的函数值。
所以对于分段函数求不定积分的题型,只要保证结果在分界点处连续,就可保证在该点处可导。【做法】
每段不定常数用 C 1 C_1 C1、 C 2 C_2 C2 表示,再根据分界点处的连续型,找出其关系,并用 C C C 表示
【例】
【真】
分段函数求不定积分的题型,考察的是分界点处的注意事项,而非单纯地求不定积分;
题干的分段被积函数在分界点处一定连续,此条件可保证所得原函数只要在分界点处连续即可保证原函数在分界点处可导。
解2:(排除法)对于选填,可用验证法,即原函数求导得被积函数;(A或D)
但需要保证原函数在x=1处连续(A排除)
选D
原则:
- 原函数求导得被积函数
- 原函数在分界点处是连续的
Temp
- 有理函数积分留数法
按照武忠祥的方式一般可以解决大多数题目,而汤家凤的留数法暂时未复习
附录
一、不定积分基本公式的证明
sec的证明