题目描述
输入一个整型数组,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
示例1:
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/lian-xu-zi-shu-zu-de-zui-da-he-lcof
1:动态规划
O(n)时间复杂度 && O(n)空间复杂度
class Solution {
public int maxSubArray(int[] nums) {
//动态规划
int[] dp = new int[nums.length];
dp[0] = nums[0];
int max = dp[0];
for(int i = 1; i<nums.length; i++){
dp[i] = Math.max(dp[i-1]+nums[i],nums[i]);
max = Math.max(dp[i],max);
}
return max;
}
}
O(n)时间复杂度 && O(1)空间复杂度
class Solution {
public int maxSubArray(int[] nums) {
int length=nums.length;
if(length==0)
return 0;
//int dp[]=new int[length]; //dp[i]表示以nums[i]结尾的子数组的最大和
// dp[0]=nums[0];
//int max=dp[0];
int max=0;
for(int i=1;i<length;i++)
{
// dp[i] =Math.max(dp[i-1],dp[i-1]+nums[i]);
nums[i] +=Math.max(nums[i-1],0);
max=Math.max(max,nums[i]);
}
return max;
}
}
因为有的时候,题目要求可能不能修改原有数组,考虑到在dp列表中,dp[i]只和dp[i-1]有关,所以用两个参数存储循环过程中的dp[i]和dp[i-1]的值即可,空间复杂度也为O(1)。 代码如下:
class Solution {
public int maxSubArray(int[] nums) {
int max = nums[0];
int former = 0;//用于记录dp[i-1]的值,对于dp[0]而言,其前面的dp[-1]=0
int cur = nums[0];//用于记录dp[i]的值
for(int num:nums){
cur = num;
if(former>0) cur +=former;
if(cur>max) max = cur;
former=cur;
}
return max;
}
}
class Solution {
public int maxSubArray(int[] nums) {
//动态规划
int dp_0 = nums[0];
int max = dp_0;
for(int i = 1; i<nums.length; i++){
dp_0 = Math.max(dp_0+nums[i], nums[i]);
max = Math.max(max, dp_0 );
}
return max;
}
}
2:贪心算法
每次观察以当前nums[i]结尾的最大和(必须包含nums[i]),要么是他自己(当他前面的最大和是负数),要么是nums[i]+之前的和
class Solution {
public int maxSubArray(int[] nums) {
int max=nums[0];
int tempMax=nums[0];
for(int i=1;i<nums.length;i++)
{
if( tempMax>=0)//如果当前tempMax的值大于0
{
tempMax=tempMax+nums[i];//那么以i结尾的数组的最大和就是tempMax+nums[i]
}
else
{
tempMax=nums[i];//如果当前tempMax的值小于0,那么以i结尾的数组的最大和就是nums[i]自己
}
max=Math.max(max,tempMax) ;//每一次都比较一下,更新max的值
}
return max;//返回max
}
}
贪心解法2
采取贪心策略,只要当前子段的和最大,就记录到res中,如果sum的结果小于0,必须将sum = 0,然后重新开始计算新的子段和,因为加上负数只会更小
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int res = INT_MIN, sum = 0;
for(int n : nums)
{
sum += n;
if(sum > res) res = sum;
if(sum < 0) sum = 0;
}
return res;
}
};
作者:zrita
链接:https://leetcode-cn.com/problems/lian-xu-zi-shu-zu-de-zui-da-he-lcof/solution/c-tan-xin-he-dp-z-by-zrita-neyq/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
3:分治算法
分治法模板:
- 定义基本情况
- 将问题分解为子问题并递归解决子问题
- 合并子问题的解以获得原始问题的解
将nums由中点mid分为三种情况:
- 最大子串在左边
- 最大子串在右边
- 最大子串跨中点,左右都有
当子串在左边或右边时,继续分中点递归分解到一个数为止,
对于递归后横跨的子串,再分治为左侧和右侧求最大子串,
可使用贪心算法求最大子串值,再合并为原始的最大子串值
int maxSubArray2(std::vector<int> &nums) {
assert(!nums.empty());
return helper(nums, 0, nums.size() - 1);
}
int helper(std::vector<int> &nums, int left, int right) {
// 分解到一个值时返回该值
if (left == right) {
return nums[left];
}
// 求中点值
int mid = left + (right - left) / 2;
// 中点左边的最大值
int leftSum = helper(nums, left, mid);
// 中点右边的最大值
int rightSum = helper(nums, mid + 1, right);
// 横跨中点的最大值
int croSum = crossSum(nums, left, right, mid);
// 返回以上三种情况中的最大值
return std::max(std::max(leftSum, rightSum), croSum);
}
int crossSum(std::vector<int> &nums, int left, int right, int mid) {
// 分解到一个值时返回该值
if (left == right) {
return nums[left];
}
// 贪心法求左边的最大值
int leftSubsum = INT_MIN;
int curSum = 0;
for (int i = mid; i > left - 1; i--) {
curSum += nums[i];
leftSubsum = std::max(leftSubsum, curSum);
}
// 贪心法求右边的最大值
int rightSubsum = INT_MIN;
curSum = 0;
for (int i = mid + 1; i < right + 1; i++) {
curSum += nums[i];
rightSubsum = std::max(rightSubsum, curSum);
}
return leftSubsum + rightSubsum;
}
作者:OOOffer
链接:https://leetcode-cn.com/problems/lian-xu-zi-shu-zu-de-zui-da-he-lcof/solution/tan-xin-fen-zhi-dong-tai-gui-hua-fa-by-luo-jing-yu/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
思路分析
若n>1,采用分治法求解最大连续子序列时,取其中间位置mid=(n-1)/2,此时序列被分成2部分,左边为[0,mid],右边为[mid+1,n-1]
该子序列只可能出现3个地方。
(1)该子序列完全落在左半部即a[0…mid]中。采用递归求出其最大连续子序列和maxLeftSum。

(2)该子序列完全落在右半部即a[mid+1…n-1]中。采用递归求出其最大连续子序列和maxRightSum.
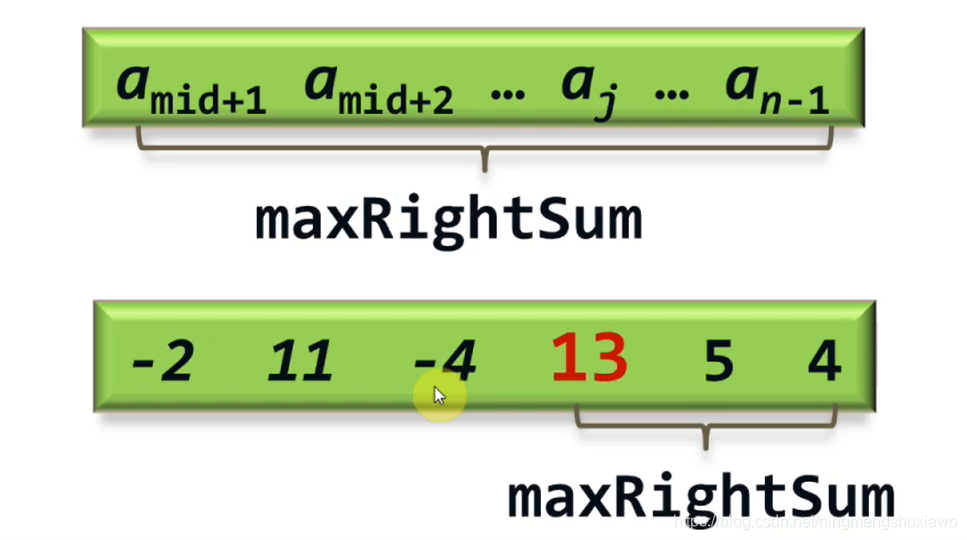
(3)该子序列跨越序列a的中部而占据左右两部分。

举例分析:
注意,下面这个例子是我看的B站的视频讲解,该题当数组全为负数时,返回0,与我们的题意不太一致,思路一样,实现代码稍作修改即可视频:chapt3-4-组合-最大连续子序列和
-
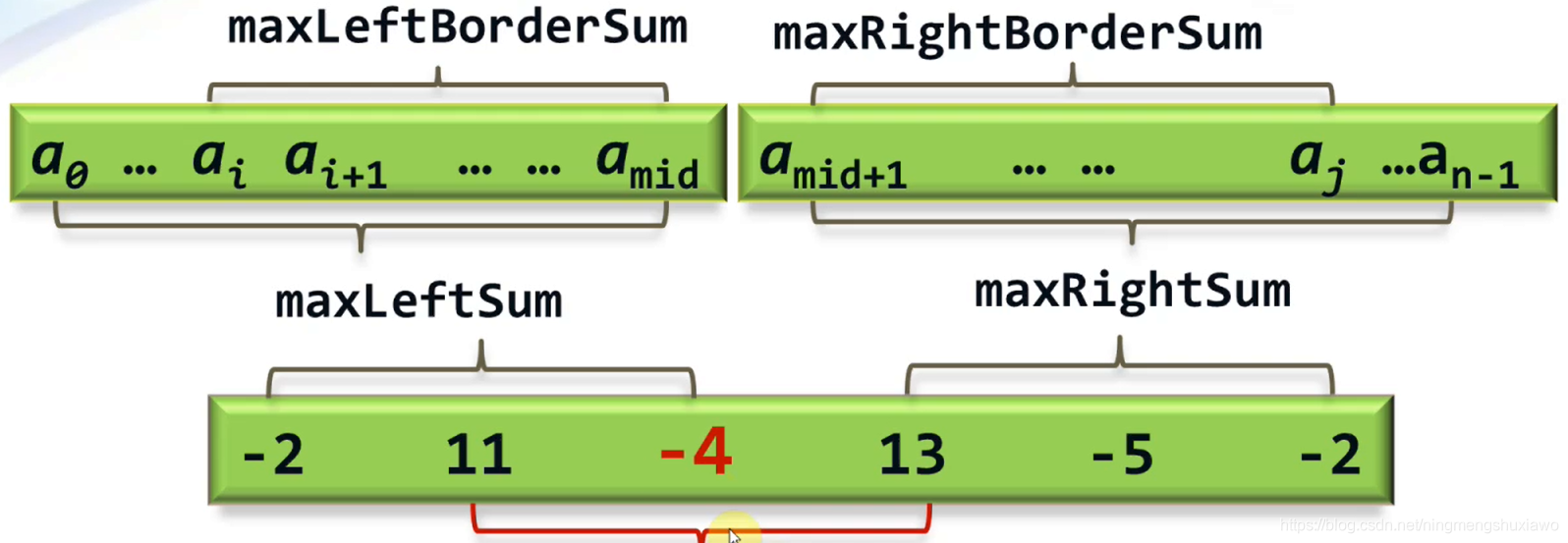
对于数组[-2,11,-4,13,-5,2],先找到中间位置,分成[-2,11,-4]和[13,-5,-2],
-
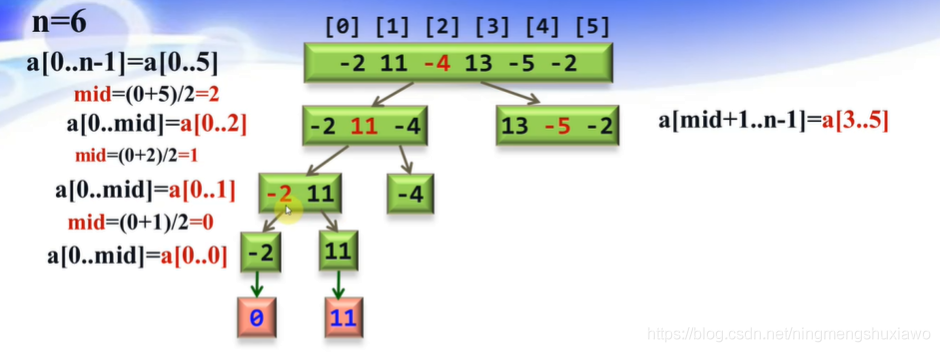
现在,先分析[-2,11,-4],继续拆分,直到每个子序列长度都为1,
-
先分成了[-2,11]和[-4],再把[-2,11]分成[-2], [11],
-
那么[-2]这个子序列,我们记其最大子序列和为0,因为它小于0嘛,[11]这个子序列,我们记其最大子序列和为11,
-
那我们就分别得到了[-2,11]的maxLeftSum,maxRightSum,还需要计算[-2,11]的maxLeftBorderSum+maxRightBorderSum
-
从下图可以看出,[-2,11]的maxLeftBorderSum+maxRightBorderSum值为11,那么对于序列[-2,11],max(maxLeftSum,maxRightSum,maxLeftBorderSum+maxRightBorderSum)=11

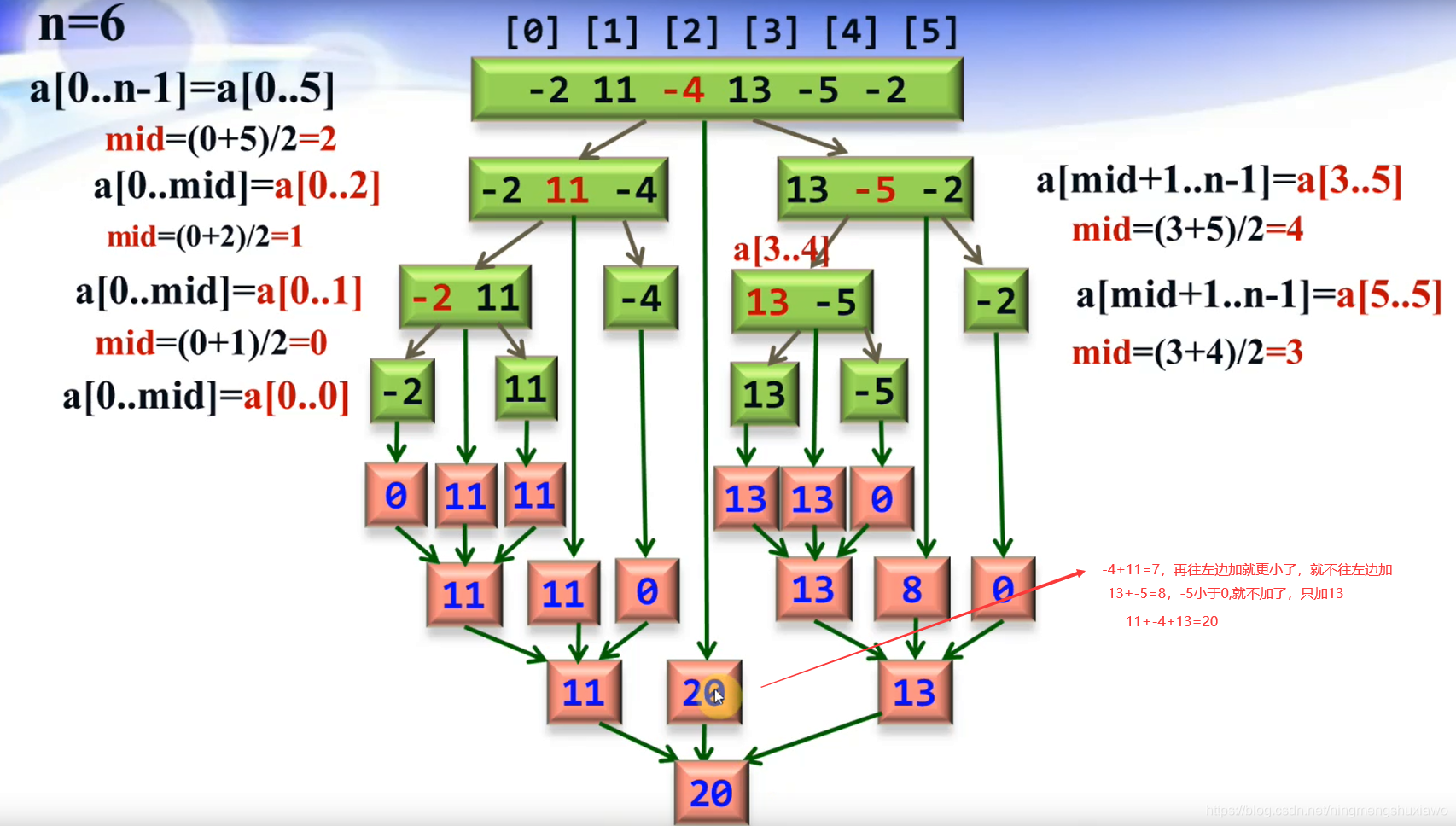
所以,对于序列[-2,11,-4,13,-5,2],max(maxLeftSum,maxRightSum,maxLeftBorderSum+maxRightBorderSum)=max(11,20,13)=20
代码实现
版本1:
class Solution {
public int maxSubArray(int[] nums) {
return maxSubArray(nums,0,nums.length-1);
}
int maxSubArray(int[]arr,int left,int right)
{
int maxLeftSum=0,maxRightSum=0;
int maxLeftBorderSum=0,maxRightBorderSum=0,LeftBorderSum=0,RightBorderSum=0;
int mid=(left+right)/2;
if(left==right)//当切分到只有一个元素
{
return arr[left];
}
maxLeftSum=maxSubArray(arr,left,mid);
maxRightSum=maxSubArray(arr,mid+1,right);
int croSum = crossSum(arr, left, right, mid);
return Math.max(Math.max( maxLeftSum,maxRightSum), croSum);
}
int crossSum(int []nums, int left, int right, int mid) {
// 分解到一个值时返回该值
if (left == right) {
return nums[left];
}
// 贪心法求左边的最大值
int leftSubsum =Integer.MIN_VALUE;
int curSum = 0;
for (int i = mid; i > left - 1; i--) {
curSum += nums[i];
leftSubsum =Math.max(leftSubsum, curSum);
}
// 贪心法求右边的最大值
int rightSubsum = Integer.MIN_VALUE;
curSum = 0;
for (int i = mid + 1; i < right + 1; i++) {
curSum += nums[i];
rightSubsum = Math.max(rightSubsum, curSum);
}
return leftSubsum + rightSubsum;
}
}
版本2:
class Solution {
public int maxSubArray(int[] nums) {
//动态规划
return maxSubArray(nums,0,nums.length-1);
}
int maxSubArray(int[]arr,int left,int right)
{
int maxLeftSum=0,maxRightSum=0;
int maxLeftBorderSum=0,maxRightBorderSum=0,LeftBorderSum=0,RightBorderSum=0;
int mid=(left+right)/2;
if(left==right)//当切分到只有一个元素
{
return arr[left];
}
maxLeftSum=maxSubArray(arr,left,mid);
maxRightSum=maxSubArray(arr,mid+1,right);
maxLeftBorderSum=Integer.MIN_VALUE;
LeftBorderSum=0;
for(int i=mid;i>=left;i--)
{
LeftBorderSum+=arr[i];
if(LeftBorderSum>maxLeftBorderSum)
{
maxLeftBorderSum=LeftBorderSum;
}
}
maxRightBorderSum=Integer.MIN_VALUE;
RightBorderSum=0;
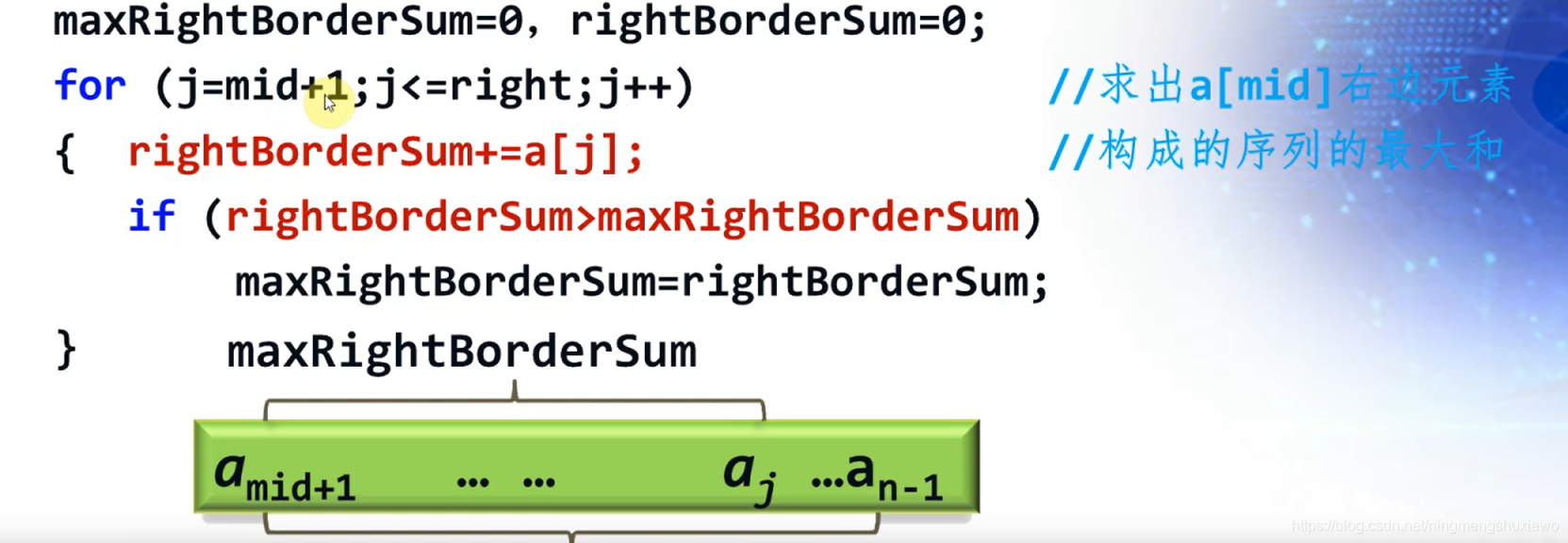
for(int j=mid+1;j<=right;j++)
{
RightBorderSum+=arr[j];
if(RightBorderSum>maxRightBorderSum)
{
maxRightBorderSum=RightBorderSum;
}
}
return Math.max(maxLeftSum,Math.max(maxRightSum, maxLeftBorderSum+maxRightBorderSum));
}
}



复杂度分析
浅谈分治算法的时间复杂度分析

在每个层上的时间复杂度为: 第在一层上是cn(c为比较一次时所用的时间), 在第二层上时数组被分成了两部分, 每部分为 n/2, 则在第二层上时间为 c * n/2 + c* n/2 = cn, 同样在第三层上, 被分成了四部分, 时间为cn/4 + cn/4 + cn/4 + cn/4 = cn. 层高一共是按刚才说的是Log2n层,每一层上都是cn, 所以共消耗时间 cn * Log2n; 则总时间:
cn * Log2n + cn = cn(1+Log2n) 即 Ѳ(nLog2n).
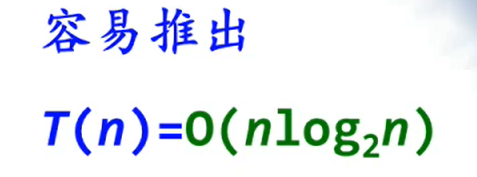
总结:
