汽车穿越沙漠的算法问题（反推法）

一、问题描述

一辆吉普车来到1000km宽的沙漠边沿。吉普车的耗油量为1L／km，总装油量为500L。显然，吉普车必须用自身油箱中的油在沙漠中设几个临时加油点，否则是通不过沙漠的。假设在沙漠边沿有充足的汽油可供使用，那么吉普车应在哪些地方、建多大的临的加油点，才能以最少的油耗穿过这块沙漠?

二.问题分析

1.为使油量消耗最少：每次出发的时候，汽车的装油量必须装满，所以每一个加油点的存油量都是汽车总装油量500L的整数倍，即500k

2.从终点倒推考虑：如果从开始点考虑的话，由于很难确定它的第一个加油点的位置，所以我们从终点出发，因为要使油耗最少，所以最后一个加油站设置的位置在距离终点500km的位置，这样最后一次刚好走完整个沙漠。

图示如下：

第一次： c1 = 500L（指的是c1至少要存储500L）距B为500KM

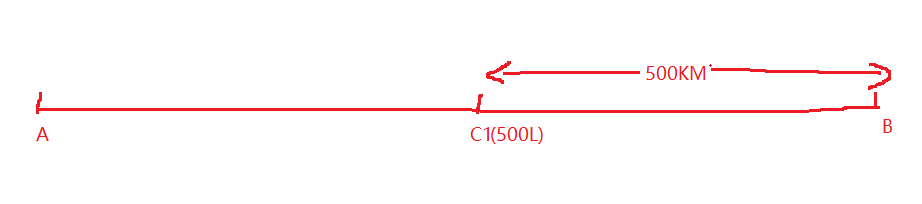
现在我们知道了倒数第一个加油点的位置，该加油点必须存储500L的油量(即k的值为1)，要从倒数第二个加油点传送500L油量给倒数第一个加油点，至少要传送两次才行（因为汽车往返要耗油，每次不能直接传500L），假设倒数第二个加油点到倒数第一个加油点的距离为Xkm,传送两次，汽车从倒数第二个加油点传油到倒数第一个加油点需要行走3倍的x距离（即3xkm），车子耗油量也是3x L，由于还要传送500L油，所以倒数第二个加油点的存油至少500+3X L,又由于每一个加油点的存量必须是500的k倍且要保证汽车油耗最少，所以取k=2，即倒数第二个加油点的存油为1000L,所以500+3x=500*2,可以得出X=500/3 km

倒数第二个加油点到倒数第一个加油点的距离为x=500/3 ，图示如下：

第二次：c2 =3 * X+c1= 2 * 500 ==> X = 500/3，距B为 (1+1/3) * 500 KM

现在计算倒数第三个加油点到倒数第二个加油点的距离，跟上面求解步骤一样，假设倒数第三个加油点到倒数第二个加油点的距离为Xkm，要从倒数第三个加油点传送1000L油量给倒数第二个加油点，至少要传三次才行，汽车从倒数第三个加油点传油到倒数第二个加油点需要行走5倍的x距离（即5xkm），车子耗油量也是5x L，由于还要传送1000L油，所以倒数第三个加油点的存油至少1000+5X L，所以k=3，即1000+5x=500*3，所以倒数第三个加油点到倒数第二个加油点的距离为x=500/5 ，倒数第三个加油点到倒数第一个加油点的距离为x=500/5，以此类推

第i次：ci = (2i-1)xi+ Ci-1 = i * 500 ==> x = (Ci-Ci-1) / (2*i - 1)=500 / (2*i - 1);

三. c语言源码

#include <stdio.h>
int main()
{
    double dis = 500,oil=500;   //油量和距离终点的距离
    int k = 1;  //初始倍数为1
    //因为不确定循环次数，又至少做一次，所以我们用do_while
    do
    {
        printf("储油点%d：距离出发点%.2lf,",k,1000-dis);    //距离开始点的距离  
        printf("储油量%d\n",(int)oil);
        k = k+1;     //倍数
        dis = dis +500.00/(2*k-1);  //dis是距离终点的距离
     
        oil = 500*k;  //为倒数第一个加油点以及每个加油点的储油量
    }while(dis<1000);

	printf("储油点%d：距离出发点%d,储油量%.2lf L\n",k,0,oil);

   // 由于总距离超过了1000km,需要重新计算第一个加油点到出发点的距离，从而得出开始点的实际的储油量
	dis=dis-500.00/(2*k-1); //减去最后一次汽车的距离，得出前n-1个加油点需要的总量

   // 计算总耗油量=前k-1个加油点需要的油量+第一个加油点到出发点的距离（即油量）
    oil = 500.00*(k-1)+(1000-dis)*(2*k-1);

	printf("\n计算实际需要出发点的储油量:\n");
    printf("储油点%d：距离出发点%d,储油量%.2lf L\n",k,0,oil);

    return 0;
}