汉诺塔C++（递归）

汉诺游戏规则如下：

1、有三根相邻的柱子，标号为A,B,C。
2、A柱子从下到上按金字塔状叠放着n个不同大小的圆盘。
3、现在把所有盘子一个一个移动到柱子B上，并且每次移动同一根柱子上都不能出现大盘子在小盘子上方。

分治算法：
1.分解 将问题分解为若干个与原题相同的子问题
2.治理 将问题不断分解到原子问题，可以直接求解为止
3.合并 将所有子问题的解合并

解决
为了解决这个问题，不妨假设已经知道怎样移动N-1个圆环了。现在，为了把起点盘A盘上的圆环移动到目标盘C盘，假设盘子分别为ABC：

1、把N-1个圆环从A盘移动到（当前）没有任何圆环的过度盘B盘；
2、把最后一个圆环从A盘移动到C盘；
3、把N-1个圆环从B盘移动到C盘（模仿1和2的操作方法来分解问题求解）。

#include<iostream>
using namespace std;
void hannoi(int n,char A,char B,char C){
    
    //n个盘子，起始位置，中转位置，终止位置 
	if(n==1){
    
    
		cout<<"将圆盘"<<n<<"从"<<A<<"移动到"<<C<<endl; //第二步 将最后一个盘子从A移动到C 
	}
	else{
    
    
		hannoi(n-1,A,C,B);  //第一步 将n-1个盘子从A移动到B 
		cout<<"将圆盘"<<n<<"从"<<A<<"移动到"<<C<<endl; 
		hannoi(n-1,B,A,C); //第三步 将n-1个盘子从B移动到C 
	}
} 
int main()
{
    
    
    int n;
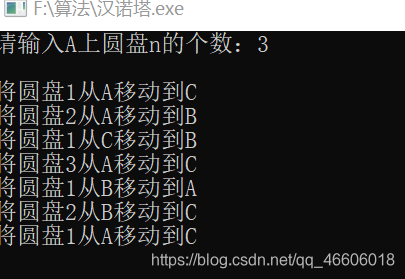
    cout<<"请输入A上圆盘n的个数：";
    cin >> n;
    cout<<endl;
    hannoi(n,'A','B','C');
    return 0;
}

看了很多别人的见解。仅作学习存档。