目录
排序基本概念:
分类:内部排序、外部排序(是否记录同时调入内存)
外部排序:多路归并排序
内部排序:(内排中只有基数排序不是比较、移动的套路)
插入排序:直接插入、折半插入、希尔(缩小增量)排序
交换排序:冒泡排序、快速排序
选择排序:简单选择排序、堆排序
归并排序
基数排序
拓补排序不是排序:)
稳定只是性质,不是优劣

Simple sorts--O(n^2)
Straight selection sort、Bubble sort、Insertion sort
More complex sorts-- O(nlogn)
Quick sort、Merge sort、Heap sort
插入排序
直接插入
挪一位比一次,时间复杂度O(n^2)
顺序链式都可,稳定
比较次数:最好n-1,最坏n(n-1)/2
(不限定排序方法,最小比较次数⌈log(2)(n!)⌉)
| Status InsertSort ( SqList &L ) { for ( i = 2; i <= L.length ; ++i ) if ( LT( L.r[i].key, L.r[i-1].key ) ) { L.r[0].key = L.r[i].key; for ( j=i-1; LT( L.r[0].key, L.r[j].key ) ; - -j ) L.r[j+1] = L.r[j]; L.r[j+1] = L.r[0]; } } //InsertSort |
折半插入排序
用折半查找优化查找的过程,时间复杂度O(n^2)
适用顺序(折半决定) ,稳定
| Status BInsertSort ( SqList &L ) { for ( i = 2; i <= L.length ; ++i ) { L.r[0] = L.r[i]; low = 1 ; high = i-1 ; while ( low <= high ) { m = ( low + high ) / 2 ; if ( LT( L.r[0].key , L.r[m]. key ) ) high = m -1 ; else low = m + 1; } for ( j=i-1; j>=high+1; - - j ) L.r[j+1] = L.r[j]; L.r[high+1] = L.r[0]; } } // BInsertSort |
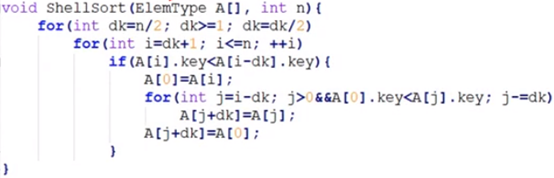
shell 排序
1、选定步长序列,如选为 8、4、2、1
2、组内采用直接插入排序,从最大步长开始,逐步减少步长,最后一次选择的的步长为 1

时间复杂度: O(n^3/2)
适用顺序结构,不稳定
题目
1.(2009真题)若数据元素序列{11,12,13,7,8,9,23,4,5}是采用下列排序方法之一得到的第二趟排序的结果,则该排序算法只能是()。
A.冒泡排序B.插入排序C.选择排序D.二路归并排序
所有元素都不在最终位置
| 排序方式 |
第一趟之后 |
| 简单选择排序 |
第一位是最小元素 |
| 起泡排序 |
最后一位是最大元素 |
| 堆排序 |
最后一位是最大元素 |
| 直接插入 |
局部有序 |
二路归并经过第二趟后应该是每4个元素有序的,但(11,12,13,7)无序
2.(2009真题)用希尔排序方法对1个数据序列进行排序时,若第1趟排序结果为9,14,13,7,8,20,23,15,则该趟排序采用的增量(间隔)可能是B
A.2B.3C.4D.5
根据增量分组,组内有序
3.给出关键字序列的直接插入、希尔排序过程
注意:
1.直接插入是从第二个数字开始比较,每一趟插入一个数字
2.希尔每一趟整理一个增量d的排序结果(最后一趟为直接插入的n合1趟,也可不用模拟,直接写出顺序序列)
交换排序
交换与插入的区别:
插入-找到最终位置,整体后移空出一个位置插入
交换-每次比较逆序都将两元素换位(泡泡上浮),若一次没换,下一次由下一个泡泡接着比对上浮
起泡排序
n个元素,通常进行n-1趟。第1趟,针对第r[1]至r[n]个元素进行。第2趟,针对第r[1]至r[n-1]个元素进行。……第n-1趟,针对第r[1]至r[2]个元素进行
时间复杂性: 正序时 O(n),逆序时 O(n^2)。平均时间复杂性 O(n^2)。
冒泡逆序比较次数:n*(n-1)/2
移动次数是比较次数的3倍,即: 3n*(n-1)/2

快速排序
基本思路
初始化标记low为划分部分第一个元素的位置,high为最后一个元素的位置,然后不断地移动两标记并交换元素
1)high向前移动找到第一个比pivot小的元素
2)low向后移动找到第一个比pivot大的元素
3)交换当前两个位置的元素
4)继续移动标记,执行1),2),3)的过程,直到low大于等于high为止

| Void QSort ( SqList &L,int low, int high ) { if ( low < high ) { pivotloc = Partition(L, low, high ) ; Qsort (L, low, pivotloc-1) ; Qsort (L, pivotloc+1, high ) } } // QSort |
| int Partition ( SqList &L,int low, int high ) { L.r[0] = L.r[low]; pivotkey = L.r[low].key; while ( low < high ) { while ( low < high && L.r[high].key >= pivotkey ) --high; L.r[low] = L.r[high]; while ( low < high && L.r[high].key <= pivotkey ) ++low; L.r[high] = L.r[low]; } L.r[low]=L.r[0]; return low; } // Partition |
快速排序在平均情况下的时间复杂性为O(nlogn)级或阶的,通常认为是在平均情况下最佳的排序方法。
题目
1. 若用冒泡排序算法对序列(10,14,26,29,41,52}从大到小排序,需进行()次比较
A.3B.10C.15D.25
5+4+3+2+1=15
冒泡逆序比较次数:n*(n-1)/2
2. 一组记录的关键码为(46,79,56,38,40,84),则利用快速排序的方法,以第一个记录为基准,从小到大得到的一次划分结果为()。
A.(38,40,46,56,79,84)B.(40,38,46,79,56,84)
C.(40,38,46,56,79,84)D.(40,38,46,84,56,79)
手动模拟快排

3. (2010真题)采用递归方式对顺序表进快速排序。下列正确的是D
A. 递归次数与初始数据的排列次序无关
B. 每次划分后,先处理较长的分区可以减少递归次数
C. 每次划分后,先处理较短的分区可以减少递归次数
D. 递归次数与每次划分后得到的分区的处理顺序无关

基本有序-O(n^2)
每次pivot为中间值-O(nlog(2)(n))
递归次数(时间复杂度)与初始排列有关,与处理顺序无关
选择排序
简单选择排序
n 个结点的结点序列,执行 n-1 次循环。每次循环时挑出具有最大或最小关键字的结点。
O(n^2)
| Void SelectSort ( SqList &L ) { for ( i =1; i < L.length; ++i ) { j = SelectMinKey ( L, i ); if ( i != j ) L.r[i] <=> L.r[j]; } } // SelectSort |
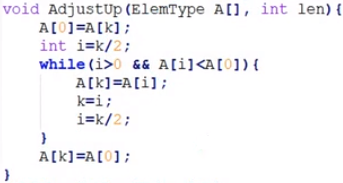
堆排序
(heap)堆:The largest element in a maximum-heap is always found in the root node
堆输出/删除: 1.Take the root (maximum即堆顶元素) element off the heap;2. Reheap(向下调整)
一般为用顺序结构存储的完全二叉树
初始化堆时从下向上调整
插入时放在末尾
时间复杂度:
建堆O(n) ,调整O ( nlogn ),整体O(n) +O ( nlogn )= O ( nlogn )
参数k为双亲结点编号


题目
1. 设线性表中毎个元素有两个数据项k1和k2,现对线性表按以下规则进行排序:先看数据项k1,k1值小的元素在前,大的在后;在k1值相同的情况下,再看k2,k2值小的在前,大的在后。满足这种要求的排序方法是()D
A.先按k1进行直接插入排序,再按k2进行简单选择排序
B.先按k2进行直接插入排序,再按k1进行简单选择排序
C.先按k1进行简单选择排序,再按k2进行直接插入排序
D.先按k2进行简单选择排序,再按k1进行直接插入排序
总序由k1决定,k1最后排,先使k2有序,再用稳定算法排k1
2.(09真题)已知关键字序列5,8,12,19,28,20,15,22是小根堆,插入关键字3,调整好后得到的小根堆是A
A.3,5,12,8,28,20,15,22,19
B.3,5,12,19,20,15,22,8,28
C.3,8,12,5,20,15,22,28,19
D.3,12,5,8,28,20,15,22,19
从最底层向上遍历。
每次选择两个孩子中更小的,与双亲比较。如果双亲大,则进行交换。
归并排序
2路归并:合并两个已排序的顺序表,比较两表中最小,取总的更小(分治思想)
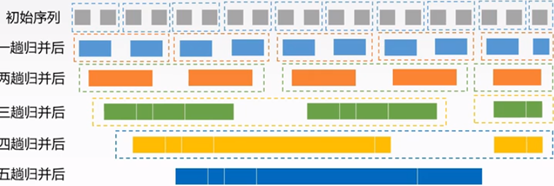
时间复杂度:合并趟数:⌈logn⌉
每趟进行比较的代价n
总的代价为 T(n) = O ( nlogn )
空间复杂度O(n)
稳定
| Void Merge ( RcdType SR[ ], RcdTypest &TR[ ], int i, int m, int n ) // 将有序的 SR[i..m] 和 SR[m+1..n] 归并为有序的 TR [ i..n] { for ( j = m+1, k= i; i <= m && j<= n; ++k ) { if ( LQ( SR[i].key , SR[i].key ) ) TR[k] = SR[ i++]; else TR[k] = SR[ j++]; } // 将 SR 中的记录由小到大依次并入到 TR if ( i <= m ) TR[k..n] = SR[ i..m]; // 将剩余的 SR[i..m] 复制到 TR if ( j <= n ) TR[k..n] = SR[ j..n]; // 将剩余的 SR[j..n] 复制到 TR } } //Merge |
递归法:
| Void MSort( RcdType SR[ ], RcdType &TR1[ ], int s, int t ) // 将 SR[s..t] 归并为 TR1 [ s..t] { if ( s == t ) TR1[s] = SR[s]; else { m = ( S+ t)/2 ; // 将SR[s..t]分为SR[s..m]和SR[m+1..t] Msort(SR,TR2,s,m); // 递归地将SR[s..m]归并为有序的TR2[s..m] Msort(SR,TR2,m+1, t); // 递归地将SR[m+1..t]归并为有序的TR2[m+1..t] Merge(TR2,TR1,s,m, t); // 将TR2[s..m]和TR2[m+1..t] 归并到TR1[s..t] } } //Msort |
| Void MergeSort( SqList &L ) // 将顺序表 L 进行归并排序 { Msort ( L.r, L.r, 1, L.length ) } //L.r 归并到 L.r自己,因为借用了TR2 } // Merge sort |
基数排序
分为最高位优先(MSD)和最低位优先(LSD一般情况)
多关键字(d元组)排序, 不基于比较
基数r限制关键字范围:0≤k<r
借助“分配”和“收集”两种操作对单逻辑关键字进行排序:
在排序时使用r个队列Q0…Qr-1
分配:开始时,各个队列置空,然后依次考察每一个结点的关键字,若aj的关键字中kij=k,就把aj放入队列Qk当中
收集:各个队列中的结点依次收尾相接,得到一个新的结点序列组成线性表
例子:324 768 270 121 962 666 857 503 768
一次分配

一次收集:270 121 962 503 324 666 857 768 768
二次分配

两次分配收集503 121 324 857 962 666 768 768 270
三次分配收集121 270 324 503 666 768 768 857 962
空间:顺序分配不合适。由于每个口袋都有可能存放所有的待排序的整数。 所以,额外空间的需求为 10n,太大了。 采用链接分配是合理的。额外空间的需 求为 n,通常再增加指向每个口袋的首尾指针就可以了。
一般情况,设每个键字的取值范围为 rd, 首尾指针共计 2×rd 个 ,总的空间 为 O( n+2×rd)
时间:关键字d 位,必须执行d趟分配收集操作。
分配的代价:O(n)分配n个元素
收集的代价:O(r)收集r个队列
总的代价为:O( d ×(n + r))
题目
1. 以下排序方法中,()在1趟结束后不一定能选出一个元素放在其最终位置上
A.简单选择排序B.冒泡排序C.归并排序D,堆排序
| 排序算法 |
第i趟后保证至少个元素归位 |
| 简单选择排序 |
是 |
| 冒泡排序 |
是 |
| 堆排序 |
是 |
| 快速排序 |
是 |
| 归并排序 |
否 |
| 插入排序 |
否 |
内部排序方法比较

时间复杂度
O(nlogn)的算法的排序(二分、递归)类似于二叉树树形结构,树高至少logn
插入、冒泡在最好情况(初始序列有序)可达n
希尔时间复杂度无法算出
快排在初始序列有序时退化到n^2
空间复杂度
快排用到递归栈
2路归并需要辅助数组n
基数排序需要r个队列
一趟排序特点
冒泡、选择、堆一趟放一个最大/小元素到最终位置
快排也可确定一个元素最终位置,但为pivot元素,非最大最小元素
应用
考虑因素:元素数目、元素大小、关键字结构及分布、稳定性、存储
结构、辅助空间等
1、若n较小时(n≤50),可采用直接插入排序或简单选择排序;若n较大时,则采用快排、堆排或归并排序
2、若η很大,记录关键字位数较少且可分解,采用基数排序
3、当文件的n个关键字随机分布,任何借助于“比较”的排序至少需要 O(nlogn)的时间
4、若初始基本有序,则采用直接插入或冒泡排序
5、当记录元素比较大,应避免大量移动的排序算法,尽量采用链式存储
题目
1. 就排序算法所用的辅助空间而言,堆排序、快速排序和归并排序的关系是
A.堆排序<快速排序<归并排序B.堆排序<归并排序<快速排序
C.堆排序>归并排序>快速排序D.堆排序>快速排序>归并排序
| 排序算法 |
空间复杂度 |
| 堆排序 |
O(1) |
| 快速排序 |
平均O(logn),最差O(n) |
| 归并排序 |
O(n) |
2.(2015真题)下列排序算法中,元素的移动次数与关键字的初始排列次序无关的是(C)。
A.直接插入排序B.起泡排序C.基数排序D.快速排序
基数排序(r为基数)算法
时间效率:基数排序需要进行d趟分配和收集,一趟分配需要O(n),一趟收集需要O(r),所以基数排序的时间复杂度为O(d(n+r),它与序列的初始状态无关
3.(2017真题)下列排序方法中,若将顺序存储更换为链式存储,则算法的时间效率会降低的是()。D
I.插入排序Ⅱ.选择排序Ⅲ.起泡排序Ⅳ.希尔排序V.堆排序
A.仅I、ⅡB.仅Ⅱ、ⅢC.仅Ⅲ、ⅣD.仅Ⅳ、V
插入排序、选择排序、起泡排序原本时间复杂度是O(n^2),更换为链式存储后的时间复杂度还是O(n^2)
希尔排序和堆排序都利用了顺序存储的随机访问特性,而链式存储不支持这种性质,所以时间复杂度会增加(时间效率降低)
外部排序
如果败者树和置换选择之前没有接触过,可能理解原理需要费些功夫
内存运行时间短,内、外存进行交换需要时间长。减少 I/O 时间成为主要矛盾。通常用归并排序
排序过程2步骤:生成合并段、外部合并(合并段调入内存,进行合并,直至最后形成一个有序的文件)
外部排序的总时间=内部排序所需时间+外存信息读写时间+内部归并所需时间
![]()
归并趟数: ⌈log(k)(m) ⌉。k 是路数;m 是初始合并段数。
平衡多路归并的性质:
k 个元素中挑选一个最小的元素需 ( k-1) 次比较。 每次比较耗费的时间代价为: tmg,
那么在进行 k 平衡归并时,总的时间耗费不会超过:logkm× ( k - 1 ) × ( n - 1 ) × tmg = log2m/ log2k × ( k - 1 ) × ( n - 1 ) × tmg
其中S趟归并需要的比较次数
![]()
改进:采用胜者树或者败者树,从 K 个元素中挑选一个最小的元素仅需 log2k次比较,这时总的时间耗费将下降:
logkm×log2k × ( n - 1 ) × tmg
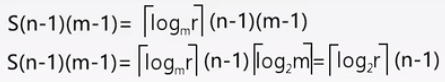
胜者树、败者树及其使用
树形选择排序的变体,为完全二叉树
胜者树:胜者进入下一轮,直至决出本次比赛的冠军。决出冠军之后,充分利用上一次比赛的结果,使得更快地挑出亚军、第三名 (空间换时间)
决出第一名需比较: k - 1次
决出第n名需比较: log2k次
败者树:每个叶结点存放各归并段在归并过程中当前参加比较的记录,内部结点用来记忆左右子树中的“失败者”,胜利者向上继续进行比较,直到根结点。
输出一个胜者后,用剩余未排序的关键字填补空缺

置换-选择排序
作用:产生尽可能长的初始归并段。
设初始待排序文件为F,初始归并段文件为FO,内存工作区为WA,内存工作区可容纳w个记录。
算法思想:
1)从待排序文件F输入W个记录到工作区WA;
2)从内存工作区WA中选出其中关键字取最小值的记录,记为MINIMAX
3)将 MINIMAX记录输出到FO中
4)若F未读完,则从F输入下一个记录到WA中;
5)从WA中所有关键字比MINIMAX记录的关键字大的记录中选出最小的关键字记录,作为新的MINIMAX;
6)重复3)~5),直到WA中选不出新的MINIMAX记录位置,由此得到个初始归并段,输出一个归并段的结束标志到FO中;
7)重复2)~6),直到WA为空。由此得到全部初始归并段
例子:设待排序文件F={17,21,05,44,10,12,56,32,29,内存工作区的容量w为3

最佳归并树
起因:由于初始归并段通常不等长。
目的:减少读写外存的次数。
归并树:m路归并,只有度为0和度为m的结点的严格m叉树
按照 HUFFMAN 树的思想,记录少的段最先合并。不够时增加虚段(权值0的结点)
WPL为读记录次数,总IO次数为2*WPL(注意WPL计算只计入叶子结点)
虚段个数确定:
设度为0的结点有N0个,度为m的结点有Nm个
则对严格m又树有N0=(m-1)Nm+1.即得Nm=(N0-1) /(m-1)
若(N0-1)%(m-1)==0,则说明对于这个N0个叶结点(初始归并段),可以构造m叉树归并树
若(N0-1)%(m-1)=u≠0,则说明对于这个N0个叶结点(初始归并段),其中有u个叶结点是多余的,单拎出来构造一棵子树的叶结点,同时还需要一个内结点作子树的根
多出u个结点,需要补充m-u-1个结点
题目
1..(2013真题)已知三叉树T中6个叶结点的权分别是2,3,4,5,6,7,T的带权(外部)路径长度最小是
A.27 B.46 C.54 D.56
u=(N0-1)%(3-1)=5%2=1≠0
需要添加m-u-1=3-1-1=1个空结点

最小的带权路径长度为(2+3)×3+(4+5)×2+(6+7)×1=46