Matlab一探DCT/IDCT变换在图像压缩中的应用

绝大多数图像都有一个共同特征，平坦区域和内容缓慢变化的区域占据一幅图像的大部分，而细节区域和内容突变区域则占小部分。也可以说，图像中直流和低频区占大部分，高频区占小部分。这样，空间域的图像变换到频域，会产生一些相关性很小的一些变换系数，可以类比不同正交方向上的系数彼此独立，前提是得找到这样一组正交向量。如果对这些系数进行压缩编码，就是变换编码。

变换中有一类叫做正交变换，可用于图像编码。自1968年利用快速傅里叶变换(FFT)进行图像编码以来，出现的了多种正交变换编码方法，比如K-L变换，离散余弦变换(DCT)等。其中，编码性能以K-L变换最理想，但缺乏快速算法，且变换矩阵随图像而异，不同图像需计算不同的变换矩阵。因而只用来参考比较。DCT编码性能最接近于K-L变换，略次而已，但它具有快速算法，广泛应用于图像编码。

DCT主要用于将数据或图像压缩，它将空域的信号变为频域上，能够以数据无关的方式去除输入信号之间的相关性，DCT变换本身是无损的，但是给接下来的量化、哈弗曼编码等创造了很好的条件，同时，由于DCT变换是对称的，我们可以在量化编码后，利用DCT反变换，在接收端恢复原始的图像信息，DCT变换在当前的图像分析领域有着极为广泛的用途，我们常见的JPEG静态图像编码以及MJPEG、MPEG动态编码等标准中都使用了DCT变换。

DCT与DFT（离散傅里叶变换）是近似相等的，后者更多的应用于信号处理领域，DCT相对简单并且在多媒体领域应用更加广泛。

典型的VPU编码解码数据处理流图：

DCT变换的数学基础

1.一维DCT变换

DCT正变换时，设

$f(x)=[f(0), f(1), f(2),\cdots, f(N-1)]^T$

对f变换后得：

$F(u)=c(u)\sum_{i=0}^{N-1}f(i)cos\bigg[ \frac{(2i+1)\pi}{2N}\cdot u\bigg] \qquad u=0,1,2,\cdots$

其中:

$c(u)=\left\{\begin{matrix} \sqrt{\frac{1}{N}},\qquad \qquad \qquad \quad u=0 \\ \\ \sqrt{\frac{2}{N}}, \qquad \ \ \ \ \ \ \ \ u=1,2,\cdots \end{matrix}\right.$

其中，f(i)为原始的信号，F(u)是经过DCT变换之后的系数，N为原始信号的点数，c(u)可以认为是一个补偿系数，可以使DCT变换矩阵为正交矩阵。

令

$A=c(u)\sum_{i=0}^{N-1}cos\bigg[ \frac{(2i+1)\pi}{2N}\cdot u\bigg]\qquad u=0,1,2,\cdots$

写成矩阵形式：

$\boldsymbol{\vec{F}=A\cdot \vec{f}}$

$A=\sqrt{\frac{2}{N}}\cdot \begin{bmatrix} \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& \cdots & \frac{1}{\sqrt{2}}\\ cos\frac{\pi}{2N}& cos\frac{3\pi}{2N}& \cdots & cos\frac{(2N-1)\pi}{2N}\\ \vdots & \vdots & \ddots & \vdots \\ cos\frac{(N-1)\pi}{2N}& cos\frac{3(N-1)\pi}{2N}& \cdots & cos\frac{(2N-1)(N-1)\pi}{2N} \end{bmatrix}$

对应的，一维余弦反变换IDCT为：

$\boldsymbol{\vec{f}=A^{-1}\cdot \vec{F}=A^T \vec{F}}$

$A^T=\sqrt{\frac{2}{N}}\cdot \begin{bmatrix} \frac{1}{\sqrt{2}}& cos\frac{\pi}{2N}& \cdots & cos\frac{(N-1)\pi}{2N}\\ \frac{1}{\sqrt{2}}& cos\frac{3\pi}{2N}& \cdots & cos\frac{3(N-1)\pi}{2N}\\ \vdots & \vdots & \ddots & \vdots \\ \frac{1}{\sqrt{2}}& cos\frac{(2N-1)\pi}{2N}& \cdots & cos\frac{(2N-1)(N-1)\pi}{2N} \end{bmatrix}$

从而将信号从频域转换为时域，由于A矩阵为正交矩阵，正交矩阵一定是满秩矩阵，所以上面的变换是无损变换，也就是说，时域和频域本质上是对同一个事物的描述，它们的信息量是相同的。

并且，形式上， $A$ 和 $A^T$ 是从具有同一个形式的公式得到的，它就是

$A(i,j)=c(u)\sum_{j=0}^{N-1}\sum_{i=0}^{N-1}cos\bigg[ \frac{(2j+1)\pi}{2N}\cdot i\bigg]$

$A^T(i,j)=c(u)\sum_{i=0}^{N-1}\sum_{j=0}^{N-1}cos\bigg[ \frac{(2j+1)\pi}{2N}\cdot i\bigg]$

这个形式上的一致对理解二维DCT变换的公式非常有帮助。

任何信号都可以由一系列的正弦信号叠加形成，一维信号是以维正弦波的叠加，二维信号是二维平面波的叠加，图像显然是二维的，二维DCT变换就是将二维图像从空间域转换到频率域，形象的说，就是计算出图像由哪些二维余弦波构成

二维余弦波

$z=cos(x)\cdot cos(y)$

的波形:

高频的 $z=cos(10x)\cdot cos(10y)$ 波形:

二维DCT变换其实是在一维DCT变换的基础上在做了一次DCT变换，其公式如下：

$F(u,v)=c(u)c(v)\sum_{i=0}^{N-1}\sum_{j=0}^{N-1}f(i,j)cos\bigg[\frac{(2i+1)\pi}{2N}u\bigg]cos\bigg[\frac{(2j+1)\pi}{2N}v\bigg]$

$c(u)=\left\{\begin{matrix} \sqrt{\frac{1}{N}},\qquad \qquad \qquad \quad u=0 \\ \\ \sqrt{\frac{2}{N}}, \qquad \ \ \ \ \ \ \ \ u=1,2,\cdots \end{matrix}\right.$

$c(v)=\left\{\begin{matrix} \sqrt{\frac{1}{N}},\qquad \qquad \qquad \quad v=0 \\ \\ \sqrt{\frac{2}{N}}, \qquad \ \ \ \ \ \ \ \ v=1,2,\cdots \end{matrix}\right.$

由公式我们可以看出，上面只讨论了二维图像数据为方阵的情况，在实际应用中，如果不是方阵的数据一般都是补齐之后再做变换的，重构之后可以去掉补齐的部分，得到原始的图像信息，这个尝试一下，应该比较容易理解。

以上公式转换为矩阵形式：

$\boldsymbol{F=AfA^T}$

$\boldsymbol{A(i,j)=c(i)\sum_{i=0}^{N-1}cos\bigg[ \frac{(2j+1)\pi}{2N}\cdot i\bigg]}$

反变换为：

$\boldsymbol{f=A^TFA}$

接下来用matlab来对这个过程模拟一遍：

clear;
clc;
macro_block_pixels=rand(4,4)*255 % 生成4x4宏块
A=zeros(4);   % 根据公式，生成转换矩阵A
for i=0:3
    for j=0:3
        if i == 0
             c = sqrt(1/4);
        else
            c = sqrt(2/4);
        end
        A(i+1, j+1) = c * cos( (j + 0.5)* pi * i / 4 ); % 生成转换矩阵
    end
end
dct_result_mannual=A*macro_block_pixels* A'; % 手搓算出来的dct系数
dct_result_matlabc=dct2(macro_block_pixels); % 调用matlab库计算出来的dct系数
diff = dct_result_matlabc-dct_result_mannual; % 输出插值矩阵

运行结果:

由上面的结果可以看出，采用的公式手搓的方法和调用Matlab dct库的方法结果是一致的，所以验证了我们方法的正确性。

不过，图片毕竟不是随机数，图像数据，像素之间，尤其是临近的像素之间，有深深的相关性在里面，怎么理解这个问题呢?

记得上大学时在自动控制原理的课堂上，老教授讲传递函数的时候，讲到一个规则，正常的传递函数的分子的最大幂一定小于分母的最大次幂，因为宏观物体都是有惯性的。这说明正常的信号一定是连续变化的，不是突变的，突变在宏观世界不会发生（微观世界就不一定了，现代量子力学证明能量都是一份一份传输的).而图像信号是宏观信号，所以像素之间是有相关性的。

而DCT变换厉害的地方在于，它不但能发现这种相关性，还能将这些相关性分解。怎么理解呢，这就好比是老板招聘员工，一个员工做事没有逻辑性，没有条理，并且非常啰嗦，他能把几件简单的事情纠缠在一起，这叫耦合性高，关联性强，抓不到重点，事情到最后肯定做成一团乱麻。而另一个人却条理分明，轻重缓急和事情之间的逻辑分的清清楚楚，他会把事情分解成几个毫不相关的部分（正交分解），然后一条条去做。

DCT就是这么神奇的算法，经过它处理后的像素数据，在变换之后，系数较大的集中在左上角，而右下角的几乎都是0，其中左上角的是低频分量，右下角的是高频分量，低频系数体现的是图像中目标的轮廓和灰度分布特性，高频系数体现的是目标形状的细节信息。DCT变换之后，能量主要集中在低频分量处，这也是DCT变换去相关性的一个体现。

之后在量化和编码阶段，我们可以采用“Z”字形编码，这样就可以得到大量的连续的0，这大大简化了编码的过程。

DCT反变换：

在图像的接收端，根据DCT变化的可逆性，我们可以通过DCT反变换恢复出原始的图像信息，其公式如下：

$f(i,j)=\sum_{u=0}^{N-1}\sum_{v=0}^{N-1}c(u)c(v)F(u,v)cos\bigg[\frac{(2i+1)\pi}{2N}u\bigg]cos\bigg[\frac{(2j+1)\pi}{2N}v\bigg]$

$c(u)=\left\{\begin{matrix} \sqrt{\frac{1}{N}},\qquad \qquad \qquad \quad u=0 \\ \\ \sqrt{\frac{2}{N}}, \qquad \ \ \ \ \ \ \ \ u=1,2,\cdots \end{matrix}\right.$

$c(v)=\left\{\begin{matrix} \sqrt{\frac{1}{N}},\qquad \qquad \qquad \quad v=0 \\ \\ \sqrt{\frac{2}{N}}, \qquad \ \ \ \ \ \ \ \ v=1,2,\cdots \end{matrix}\right.$

同样的道理, 利用之前的矩阵运算公司可以推导出DCT反变换相应的矩阵形式：

$\boldsymbol{F=AfA^T}$

$\boldsymbol{f=A^{-1}fA=A^TfA}$

继续用matlab来仿真这个过程：

clear;
clc;
macro_block_pixels=rand(4,4)*255 % 生成4x4宏块
A=zeros(4);   % 根据公式，生成转换矩阵A
for i=0:3
    for j=0:3
        if i == 0
             c = sqrt(1/4);
        else
            c = sqrt(2/4);
        end
        A(i+1, j+1) = c * cos( (j + 0.5)* pi * i / 4 ); % 生成转换矩阵
    end
end
dct_result_mannual=A*macro_block_pixels* A'; % 手搓算出来的dct系数
dct_result_matlabc=dct2(macro_block_pixels); % 调用matlab库计算出来的dct系数
diff = dct_result_matlabc-dct_result_mannual; % 输出插值矩阵
restore= A'*dct_result_matlabc*A; % dct反变换得到原始值.

我们可以看到反变换后无损的恢复了原始信息，所以证明了方法的正确性。但是在实际过程中，需要量化编码或者直接舍弃高频分量等处理，所以会出现一定程度的误差，这个是不可避免的，所以才叫图像压缩吧，否则DCT后所有的系数都保留的话，岂不是和原来的灰度图像有同样的数据量，就不存在压缩了。

使用DCT算法来压缩一张图片：

前面都是理论的东西，现在用DCT算法来压缩一张图片.在实际的图像处理中，DCT变换的复杂度其实是比较高的，为了节省存储和算力，通常的做法是，将图像进行分块，然后在每一块中对图像进行DCT变换和反变换，在合并分块，从而提升变换的效率。具体的分块过程中，随着子块的变大，算法复杂度急速上升，但是采用较大的分块会明显减少图像分块效应，所以，这里面需要做一个折中，在通常使用时，大都采用的是8*8的分块。

Matlab的 blkproc 函数可以帮我们很方便的进行分块处理，下面给出我们的处理过程：

clc;clear;
img = rgb2gray(imread('D:\woman.jpg'));
figure, imshow(img); 
h=figure(1);
set(h,'name','original girl','Numbertitle','off')

% 1，使图像行列为 8的倍数
[row,col] = size(img);
row = round(row/8) * 8; 
col = round(col/8) * 8;
img = imresize(img, [row, col]);

% 2，对图像块进行dct变换
img_dct = zeros(row, col); % 存放转换后的dct系数
for i=1:8:row-7
    for j=1:8:col-7
        img_block = img(i:i+7, j:j+7);
        dct_block = dct2(img_block); % 也可用刚才实现的(定义成一个函数即可)
        img_dct(i:i+7, j:j+7) = dct_block;
    end
end
figure, imshow(img_dct); % 显示生成的dct系数
o=figure(2);
set(o,'name','dct coefficent girl','Numbertitle','off')

% 3，dct反变换
new_img = zeros(row,col);
for i=1:8:row-7
    for j=1:8:col-7
        dct_block = img_dct(i:i+7, j:j+7);
        img_block = idct2(dct_block); % 也可用刚才实现的(定义成一个函数即可)
        new_img(i:i+7, j:j+7) = img_block;
    end
end
figure,  imshow(mat2gray(new_img)); % 显示反变换回来的图像
r=figure(3);
set(r,'name','restore the girl','Numbertitle','off')

中间图片是DCT值的灰度显示，可以看到美女经过变换和反变换后，音容宛在。。。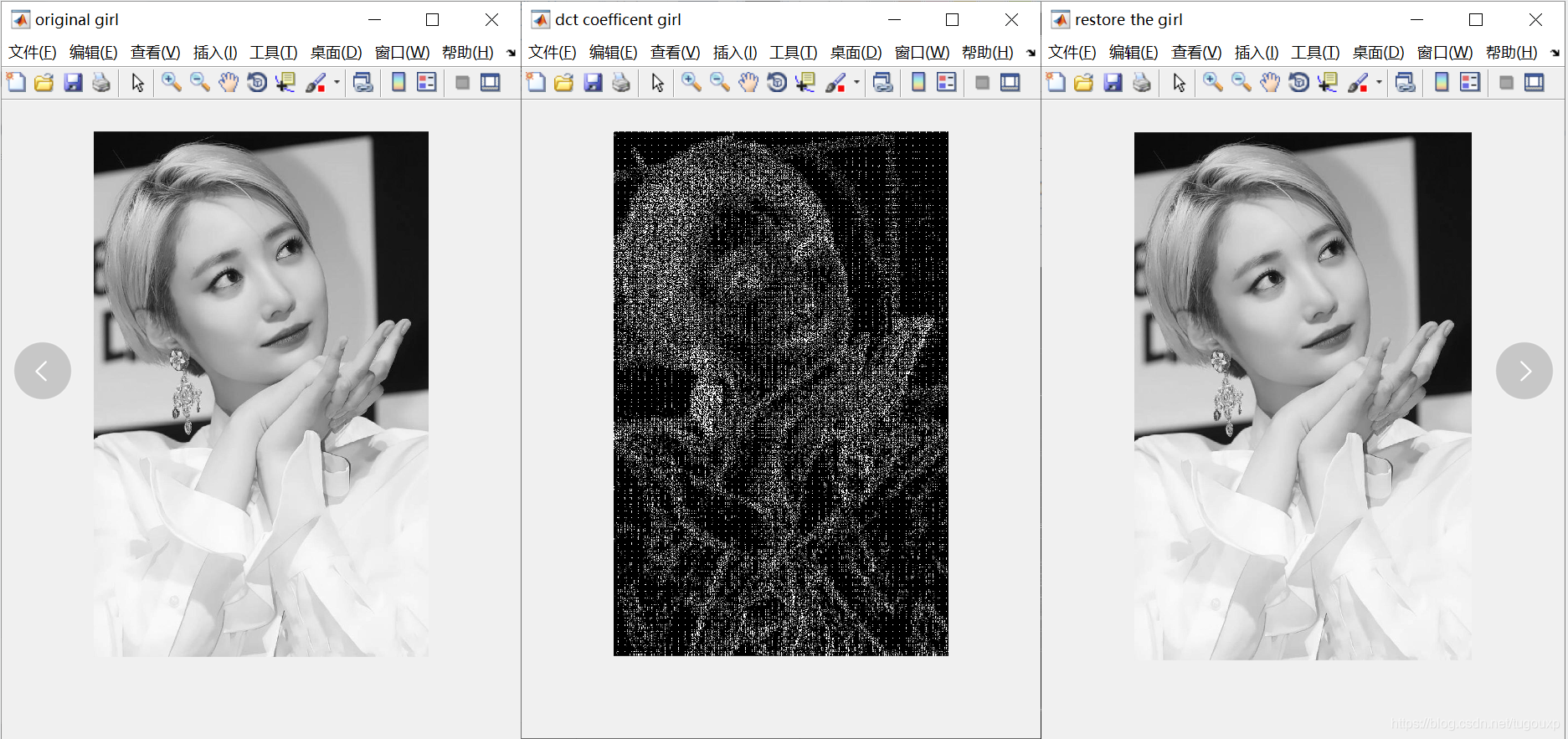

不分块DCT变换:

对于图像变换编码，最理想的变换操作应对整个图像进行，以便去除所有像素间的相关性，但这样的操作计算量太大，实际上，往往把图像分为若干块，以块为单位进行DCT变换。

代码：

clc;clear;
img = rgb2gray(imread('D:\woman.jpg'));
figure, imshow(img); 
h=figure(1);
set(h,'name','original girl','Numbertitle','off')

% 1，使图像行列为 8的倍数
[row,col] = size(img);
col=row;
img = imresize(img, [row, col]);

% 2，对图像块进行dct变换
img_dct = zeros(row, col); % 存放转换后的dct系数
img_block = img;
dct_block = dct2(img_block); % 也可用刚才实现的(定义成一个函数即可)
img_dct= dct_block;
figure, imshow(img_dct); % 显示生成的dct系数
o=figure(2);
set(o,'name','dct coefficent girl','Numbertitle','off')

% 3，dct反变换
new_img = zeros(row,col);
new_img = idct2(img_dct); % 也可用刚才实现的(定义成一个函数即可)

figure,  imshow(mat2gray(new_img)); % 显示反变换回来的图像
r=figure(3);
set(r,'name','restore the girl','Numbertitle','off')

单张图片为一个宏块儿，为了保证变换矩阵是方阵，这里不得不对美女进行了宽方向上的拉伸，和原图比很明显能看出来变“胖”了。

左上角大，右下角小：

多看美女有助于提高研发效率：

结束！

Matlab一探DCT/IDCT变换在图像压缩中的应用

DCT变换的数学基础

猜你喜欢