2019江西省赛 A题 hdu6567 树的重心

http://acm.hdu.edu.cn/showproblem.php?pid=6567

• 以一棵树的任意一个节点作为根，则可以形成一棵有根树，如果以此根为界的若干棵子树中，最大子树具有的节点数最小，那么这个节点就是树的重心
• 树的重心相当于树的平衡点，一棵树最少有一个重心，最多有两个重心，如果有两个重心，那它们肯定直接相连，这是显然的，能够简单证明

这道题的意思是给你一个$n$，表示总共有多少个节点，然后给出$n-2$条边，表示两棵树内部的父子关系，这两棵树不相连，现在让你加一条线，把这两棵树连起来，给定一个函数${\sum }_{i=1}^n{\sum }_{j=i+1}^{n}dis(i,j)$，其中$dis$函数表示从$i$到$j$的路径边的数量，问你最少是多少

• 这道题最优解是把两棵树的重心连起来，为什么？因为一棵树内部怎么连距离都一样，关键在于两棵树之间，如果不连重心，这个值会变大，因为重心才是让所有子树节点数最少的关键点
• 其实重心是树上很重要的一个点，也不难想到这一层
• 那么就是一个裸的求重心问题了，在这里复习一下树的重心
  
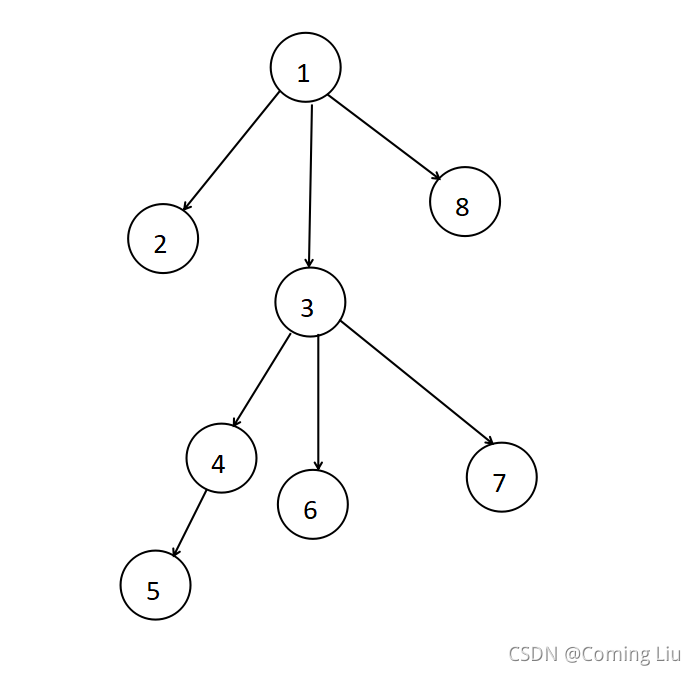
  图中$3$应该是树的重心，怎么求的？就是这样，如下图
  
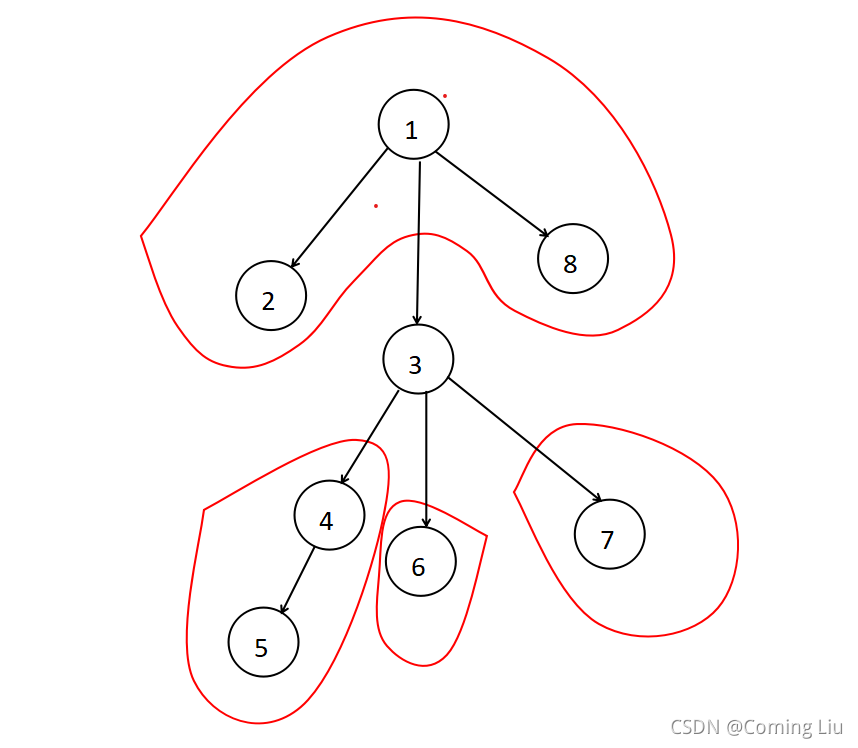
  就是看当前节点的子树中最大的部分和他上方的部分之间节点数最大是多少，这就是当前节点的最大子树具有的节点数，需要注意的是我们要取所有子树的最大值，所以这里要使用一次$Dfs$来实现，然后再取此节点上方的节点数，这只需要用总共的节点数量减去以当前节点为根的节点数量即可
• 那么本题思路和过程如下，首先求两棵树重心，然后连接，这时候从任意一个节点进入$Dfs$，求以所有节点为根的子树数量，设$sz[i]$表示以$i$为根的子树节点数量，那么答案应该是$\sum sz[i]\times (n-sz[i])$。这里如果用暴力搜索，复杂度是$O(n^2)$的，不行，换根或许可以，但是更好的办法是考虑每条边的贡献来源，比如说上图里面的边$1\to 3$，从节点$1,2,8$出发到以$3$为根的子树都需要经过这条边，所以贡献就是$3\times 5=15$，因为彼此之间至少要连一条边，问题中$j$是从$i+1$开始的，所以这样对每一条边算贡献得到的就是最终答案，即上述公式。如果问题要求$j$从$1$开始可能就是需要$\times 2$了
• 上述即为求树上任意两点之间距离和的过程，其余部分都是树上$dp$基础知识，不提。程序如下

#include <bits/stdc++.h>

using namespace std;

const int MAXN = 3e5 + 100;
typedef long long ll;
struct Edge{
    
    
    int next;
    int to;
    int val;
}edge[MAXN];
int head[MAXN];
int cnt;
void Add_Edge(int u, int v, int w){
    
    
    edge[cnt].next = head[u];
    edge[cnt].to = v;
    edge[cnt].val = w;
    head[u] = cnt++;
}
ll sz[MAXN];
int vis[MAXN];
int tot;
void Dfs1(int u, int fa){
    
    
    sz[u] = 1;
    vis[u] = 1;
    tot += 1;
    for(int i=head[u];~i;i=edge[i].next){
    
    
        int v = edge[i].to;
        if(v == fa) continue;
        Dfs1(v, u);
        sz[u] += sz[v];
    }
}
int root;
ll res = __LONG_LONG_MAX__;
ll Dfs2(int u, int fa){
    
    
    ll num = 1;
    ll sum = 0;
    for(int i=head[u];~i;i=edge[i].next){
    
    
        int v = edge[i].to;
        if(v == fa) continue;
        ll s = Dfs2(v, u);
        sum = max(sum, s);
        num += s;
    }
    ll p = max(sum, tot - num);
    if(p < res){
    
    
        res = p;
        root = u;
    }
    return num;
}
ll ans = 0;
void solve(int u, int fa, ll n){
    
    
    sz[u] = 1;
    for(int i=head[u];~i;i=edge[i].next){
    
    
        int v = edge[i].to;
        if(v == fa) continue;
        solve(v, u, n);
        sz[u] += sz[v];
    }
    ans += sz[u] * (n - sz[u]);
}
int main(){
    
    
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n, u, v;
    memset(head, -1, sizeof head);
    cin >> n;
    for(int i=2;i<n;i++){
    
    
        cin >> u >> v;
        Add_Edge(u, v, 1);
        Add_Edge(v, u, 1);
    }
    Dfs1(1, -1);
    Dfs2(1, -1);
    int rootone = root;
    int roottwo = 1;
    for(int i=1;i<=n;i++){
    
    
        if(!vis[i]){
    
    
            roottwo = i;
            break;
        }
    }
    res = __LONG_LONG_MAX__;
    tot = 0;
    Dfs1(roottwo, -1);
    Dfs2(roottwo, -1);
    roottwo = root;
    Add_Edge(rootone, roottwo, 1);
    Add_Edge(roottwo, rootone, 1);
    solve(1, -1, n * 1ll);
    cout << ans << '\n';
    return 0;
}

可参考视频讲解，讲的很好，转发推广一下
https://www.bilibili.com/video/BV14K4y1f7Uf