1、行缩减和逆矩阵
当我们对方程组 进行行归约时,每一步都是一个基本的行操作:
将第 行乘以常数
,
将第行的
加到第
行,或
交换第 i 行和第 j 行。
这些都可以通过取一个相应的初等矩阵 来描述,并将方程
的两边乘以
,从左边开始,得到
。这是一个实际操作的示例,其中基本行操作是“从第三行减去第一行的两倍”:

许多这些基本矩阵的乘积是其他一些更复杂的矩阵。因此,我们通过行操作从 得到的每个方程组都将具有
的形式,对于某些矩阵
。单个矩阵可以概括任意多个行操作的组成。
特别是,我们可能关心哪个矩阵 M 对应于对矩阵进行行约简的行操作。 那么,它是哪个矩阵?为了回答这个问题,我们首先将系统的列拆分为基本变量 和非基本变量
,就像我们在上一节中所说的。
当我们对矩阵 A 相对于 B 进行行归约时,我们的目标是让第 i 个基本变量在第 i 行中具有 1,在所有其他行中具有 0。换句话说,在得到的行缩减系统 的矩阵
中,对应于基本变量的列
正好形成单位矩阵
。
这足以告诉我们 M 必须是什么。如果将所有 左乘
得到一个矩阵
,其子矩阵
等于
,那么仅将子矩阵
左乘
就应该得到
。但是只有一个矩阵具有这种效果:它是逆矩阵
。
因此,当我们对基本变量 的系统
进行行归约时,我们得到的新方程组(相当于旧的,但形式更好)是
.
另一种思考发生了什么的方法,考虑将系统 拆分为
![]()
然后,我们可以通过乘以 并重新排列以
形式求解
:

这为我们提供了 的所有解的公式:我们可以为
选择任何我们喜欢的值,然后我们必须使用上面的公式来找到与之对应的
的值。
特别是,我们可以设置 ,然后公式给我们
:这就是我们所说的基本解。
2、单纯形表的公式
这在单纯形表中看起来如何?同样,我们假设我们的线性程序具有以下形式
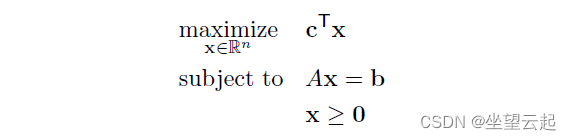
其中 A 是一个矩阵,
,
; A 的行是线性独立的。
如果发生以下两种情况,则基本变量 B 的每个选择都会产生一个有效的单纯形表:
是可逆的:然后通过设置
和
,我们得到一个基本的解决方案。
:那么,我们得到的基本解决方案是可行的。
为了使单纯形表看起来“更干净”,我们可以对列进行排序,将基本变量 放到最前面 和
放在最后:然后,表看起来像

对于矩阵 ,向量
和
,以及标量
。
通常,在实践中,我们不对列进行排序,因此看起来略有不同。 但是交换列并没有什么坏处,只要我们保持它们的标签。 例如,对于线性程序
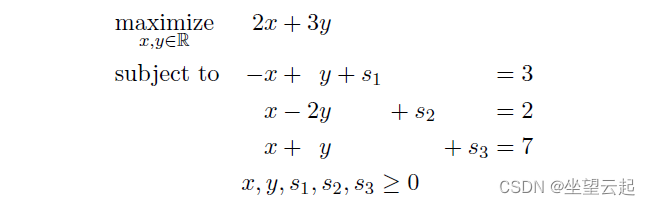
我们在第 5 讲中看到的,当我们解决它时,我们得到了下面左边的画面,但我们可以把它写成右边的“清理形式”。

我们如何仅通过知道问题以及我们选择了哪些基本变量 来找到
、
、
和
的值?
让我们从 开始。这是表格的右侧,保存当前基本可行解中基本变量的值。换句话说,这正是我们从公式
得到的。 在上面的问题中,如果我们首先将 A 重新排列为一个矩阵
,该矩阵将按
,
,
,
,
排序,我们得到:

我们还知道,从 开始到上图结束所需的行减少步骤可以用
的左乘代替。当我们将表格的
部分乘以
时,我们得到了大单位矩阵。当我们将表格的
部分乘以
时,我们得到了我们想要的公式的矩阵
。 所以
; 在我们的示例中,
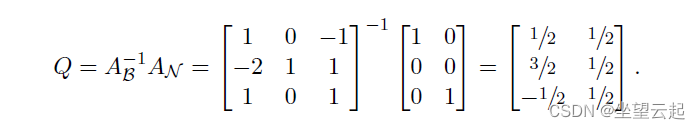
由 、
和
组成的降低成本行呢?其中,
更容易找到:它是目标值。 一般来说,我们的目标值是
,我们可以将其分为两部分:
。
在我们当前的基本解中, 和
。因此
是当前目标值; 这就是
的公式。 就
而言,我们有
。
为了找到 ,让我们考虑一下降低成本行的来源。通常,我们一次计算一个行操作,因为我们从一个基本可行的解决方案转移到另一个。 但是我们总是可以从头开始计算减少的成本行:从原始成本行(即向量
)开始并对其进行行减少以消除枢轴下方的条目。
替换表格中的 的大矩阵(由
和
组成)由
给出。(或者,
,如果我们决定重新排列列以将基本变量放在首位。)为了消除基本变量以下的成本,我们分两步进行:
取这个矩阵 并左乘
,得到一个与基本变量分量中的
相匹配的向量。
从 中减去这个向量,得到一个在基本变量组件中为零的向量,并且在非基本变量组件中降低了成本。
在我们的例子中,第一步给了我们
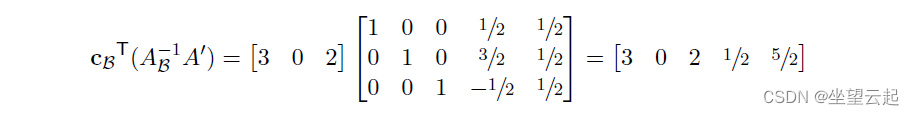
当我们从 中减去它时(也重新排序以匹配我们的新变量顺序),我们得到
![]()
所以我们的表格最下面一行的公式是。
有两种使用方法。 首先,我们可以得到一个特定变量的降低成本:如果 是
对应于变量
的列,那么它的降低成本
由下式给出
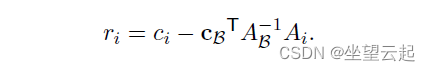
其次,我们可以通过公式得到所有非基本减少成本

您可能已经注意到向量 经常出现在这里。给它起一个名字
并在我们发现成本降低时计算它会很方便。 我们将在本课程后面看到向量
的更多属性!
总而言之,以下是单纯形表各部分的公式:
