1.软件版本
matlab2017b
2.系统概述
·PID控制器:
PID控制器(比例-积分-微分控制器),由比例单元 P、积分单元 I 和微分单元 D 组成。通过Kp, Ki和Kd三个参数的设定。PID控制器主要适用于基本线性和动态特性不随时间变化的系统。
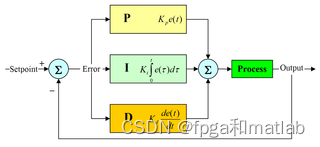
PID 控制器的方块图PID 控制器是一个在工业控制应用中常见的反馈回路部件。这个控制器把收集到的数据和一个参考值进行比较,然后把这个差别用于计算新的输入值,这个新的输入值的目的是可以让系统的数据达到或者保持在参考值。和其他简单的控制运算不同,PID控制器可以根据历史数据和差别的出现率来调整输入值,这样可以使系统更加准确,更加稳定。可以通过数学的方法证明,在其他控制方法导致系统有稳定误差或过程反复的情况下,一个PID反馈回路却可以保持系统的稳定。
PID控制的基本原理和常用形式及数学模型:
具有比例-积分-微分控制规律的控制器,称PID控制器。这种组合具有三种基本规律各自的特点,其运动方程为:
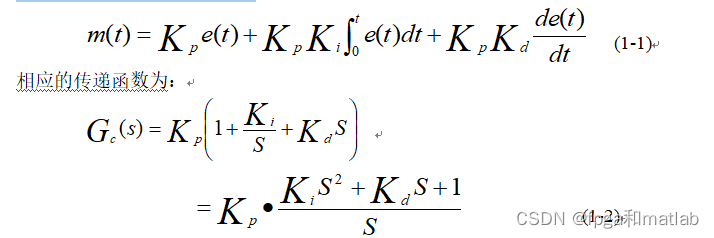
PID控制的结构图为:
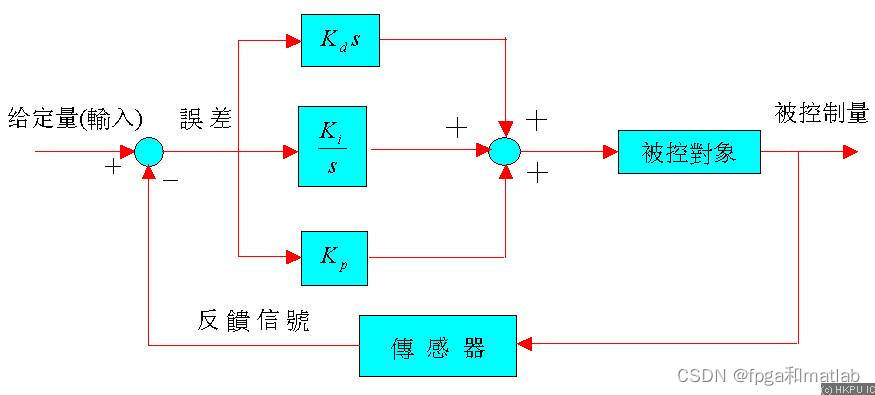

由此可见,当利用PID控制器进行串联校正时,除可使系统的型别提高一级外,还将提供两个负实零点。与PI控制器相比,PID控制器除了同样具有提高系统的稳态性能的优点外,还多提供一个负实零点,从而在提高系统动态性能方面,具有更大的优越性。因此,在工业过程控制系统中,广泛使用PID控制器。PID控制器各部分参数的选择,在系统现场调试中最后确定。通常,应使积分部分发生在系统频率特性的低频段,以提高系统的稳态性能;而使微分部分发生在系统频率特性的中频段,以改善系统的动态性能。
·H无穷控制器:
H∞控制是一种具有很好鲁棒性的设计方法,具有设计思想明确、控制效果好等优点,尤其适用于模型摄动的多输入多输出(MIMO)系统。H∞控制在控制理论、设计方法及应用等方面,经过多年不断发展和完善,已成为一种具有较完整体系的鲁棒控制理论。为适应控制系统稳定性、自适应性、智能化及工程化的更高要求,基于线性矩阵不等式(LMI)的H∞控制、非线性H∞控制以及H∞控制与神经网络和模糊控制结合,成为近年来H∞控制研究的热点。随着H∞控制研究的深入,其存在的诸如理论复杂、计算量大和参数摄动范围有限等问题将会逐步得到解决,适用范围也会更广、应用前景会更好。
3.部分程序
程序设计部分主要分为四个部分:
第一个是伺服电机
第二个是H无穷控制器
第三个是用来对对比的PID控制器
第四个是GUI界面(封装之后成toolkit进行调用)
最后编写的m文件一共分如下几个部分:
基于PID控制的伺服电机系统
基于H无穷控制的伺服电机系统
封装后成为toolkit之后的GUI界面系统。
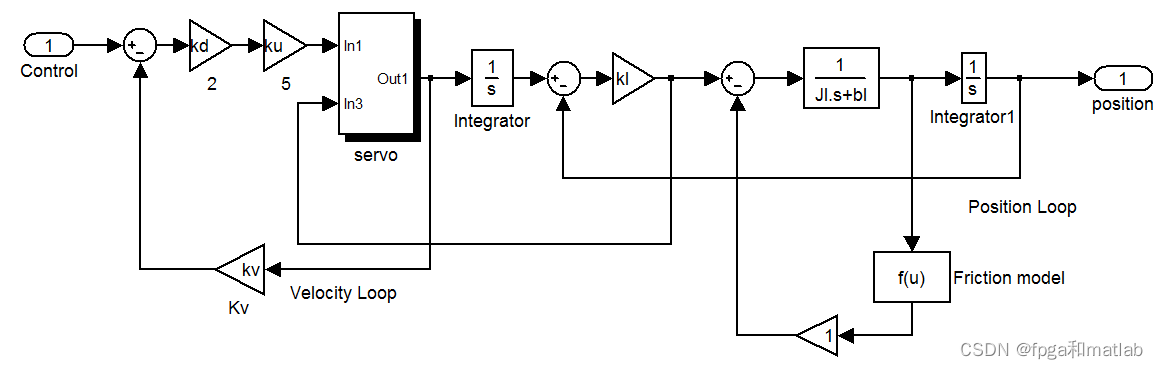
一个伺服系统,其主要涉及到的对象参数为:
Ku:功率放大器的放大系数
R:电枢电阻
Km:电动机力矩系数
Ce:电压反馈系数
J:转动惯量
theta:转速
r:指令信号
u:控制输入
F:驱动力
完整的伺服模型如下所示:
clc;
clear all;
close all;
warning off;
%步骤一:定义模型
ts = 0.001;
J = 0.05;
q = 0.1;
sys = tf(1,[J,q,0]);
dsys = c2d(sys,ts,'z');
[num,den] = tfdata(dsys,'v');
%步骤二:权值函数的选择
G = sys/10000000;
%加权函数1
nw1 = [0.25,1 ,0.5];
dw1 = [0.9 ,1.7,0.4];
[m1,p1,w1]= bode(tf(nw1,dw1));
%加权函数2
nw2 = [1,0,0];
dw2 = [0,0,300];
[m2,p2,w2]= bode(tf(nw2,dw2));
figure;
subplot(211);
semilogx(w1,20*log10(m1(:)));
title('Weight function 1');
subplot(212);
semilogx(w2,20*log10(m2(:)));
title('Weight function 2');
%步骤三:H无穷最优选择
[a,b,c,d] = tf2ss(num,den);
s = mksys(a,b,c,d);
w1 = [nw1;dw1];
w2 = [nw2;dw2];
Tss = augtf(s,w1,[],w2);
[gg,cFopt,ccL] = hinfopt(Tss);
disp('the opt gamma value:');
gg
[af,bf,cf,df] = branch(cFopt);
Gc = zpk(ss(af,bf,cf,df));
G0 = G*Gc;
Gc1 = feedback(G0,1);
%步骤四:测试
t = 0:0.1:100;
y = step(Gc1,t);
figure;
time = 1/length(t):1/length(t):1;
plot(time,y);
grid on;
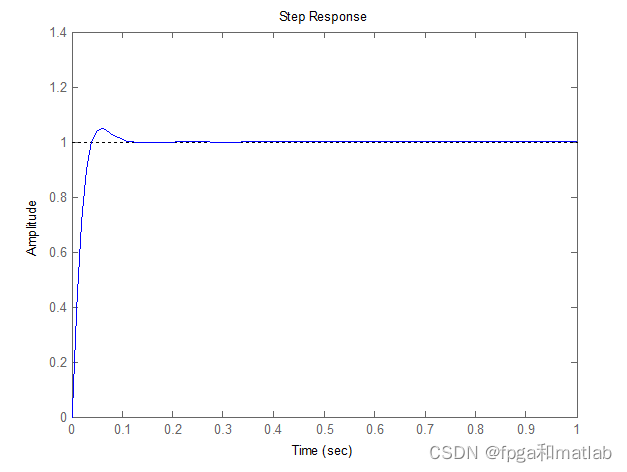
4.仿真结论

A08-21