题目
如下图的九宫格中,放着 1 ~ 8 的数字卡片,还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。 经过若干次移动,可以形成图 2 所示的局面。
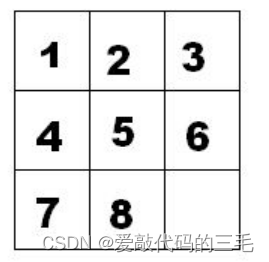
我们把上图的局面记为:12345678.
把下图的局面记为:123.46758
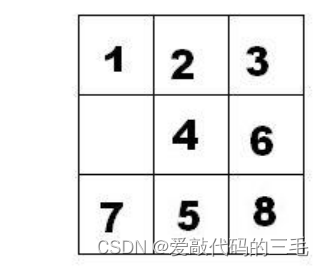
显然是按从上到下,从左到右的顺序记录数字,空格记为句点。
题目的任务是已知九宫的初态和终态,求最少经过多少步的移动可以到达。如果无论多少步都无法到达,则输出 -1。
输入描述
输入第一行包含九宫的初态,第二行包含九宫的终态。
输出描述
输出最少的步数,如果不存在方案,则输出 -1。
输入
12345678.
123.46758
输出
3
思路
求最少步数,典型的广搜
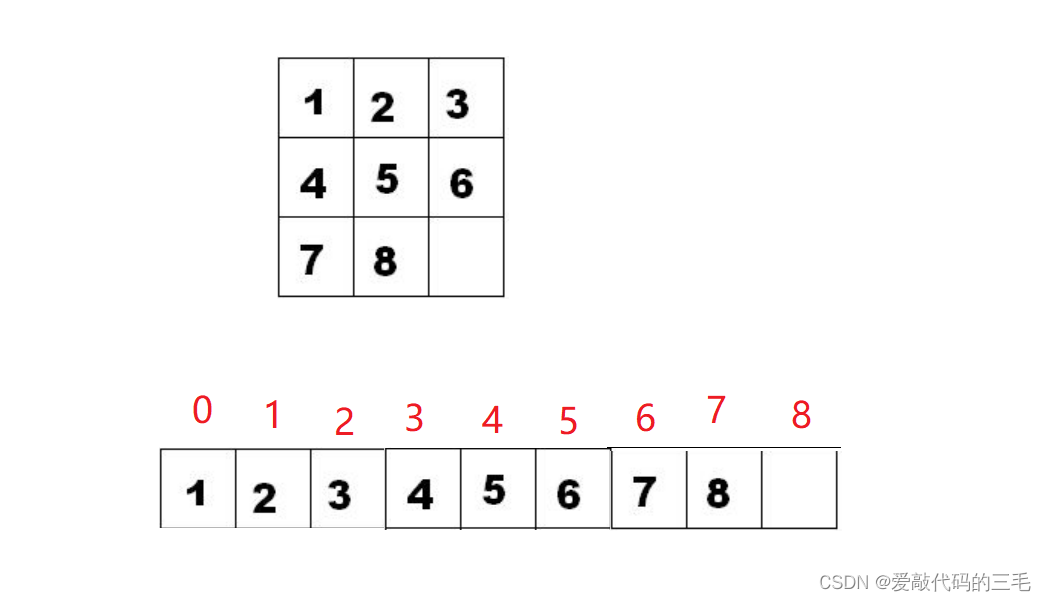
- 题目让我们求最少步数,我们可以模拟空格的移动
- 通过字符串的下标交换字符位置,模拟字符串的上下左右的移动,每次移动通过set判断该状态是否已经移动过,如果没有就入队列
- 上(-3)下(+3)左(-1)右(+1)
- 判断每次的下标是否合法,越界只要判断示是否在字符串长度范围内
关键代码:
(pos%3 != index%3 && pos/3 != index/3)
因为当前位置和上下都只是差3,左右都只是差1
如果是左右就一定满足,下标/3相等
如果是上下就一定满足,下标%3相等
代码
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String start = sc.next();
String end = sc.next();
// 枚举字符串下标的上下左右
int[] upDownLeftRight = {
-3,3,-1,1};
// 去重
Set<String> set = new HashSet<>();
Queue<String> queue = new LinkedList<>();
set.add(start);
queue.offer(start);
int count = 0;
// 标记是否已经找到
boolean flag = false;
while (!queue.isEmpty()) {
int size = queue.size();
while (size-- != 0) {
String s = queue.peek();
// 空格位置
int index = s.indexOf(".");
for (int i = 0; i < 4; i++) {
int pos = index + upDownLeftRight[i];
// 当新的位置不是空格的上下左右或者已经越界
if (pos < 0 || pos > 8 || (pos%3 != index%3 && pos/3 != index/3)) {
continue;
}
char c = s.charAt(pos);
char[] ch = s.toCharArray();
ch[pos] = ch[index];
ch[index] = c;
String str = new String(ch);
if (str.equals(end)) {
flag = true;
break;
}
if (set.add(str)) {
queue.offer(str);
}
}
queue.poll();
}
count++;
if (flag) {
break;
}
}
if (flag) {
System.out.println(count);
} else {
System.out.println(-1);
}
}
}